§ 1.3 Среднее и действующее значения синусоидально изменяющейся величины. Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за полпериода. Среднее значение тока
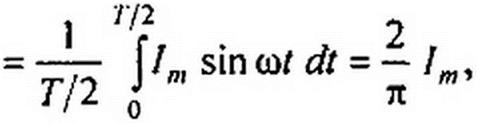 |
|
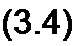 |
т. е. среднее значение синусоидального тока составляет 2/л = 0,638 от амплитудного. Аналогично, £ср = 2 Ет /п; Ucp =2U„,/ я.
Широко применяют понятие действующего значения синусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным). Действующее значение тока
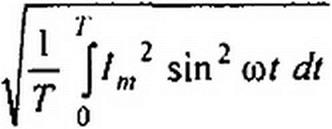 | |||||
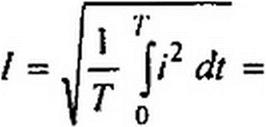 | |||||
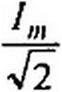 | |||||
|
Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного. Аналогично
£ = £„,/72 и U = Uml&.
Можно сопоставить тепловое действие синусоидального тока с тепловым действием постоянного тока, текущего то же время по тому же сопротивлению.
Количество'теплоты, выделенное за один период синусоидальным током,
'\Ri2dt = RliL о z
Выделенная за то же время постоянным током теплота равна Rl^ Т.
Приравняем их:
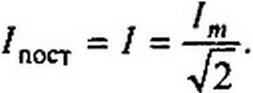 |
|
Таким образом, действующее значение синусоидального тока / численно равно значению такого постоянного тока, который за время, рав-
ное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.
Большинство измерительных приборов показывают действующее значение измеряемой величины**.
§ 3.3 Коэффициент амплитуды и коэффициент формы. Коэффициент амплитуды ка — это отношение амплитуды периодически изменяющейся функции к ее действующему значению. Для синусоидального тока
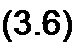 Ла=/„// = >/2.
Ла=/„// = >/2.
Под коэффициентом формы к$ понимают отношение действующего значения периодически изменяющейся функции к ее среднему за полпериода значению. Для синусоидального тока
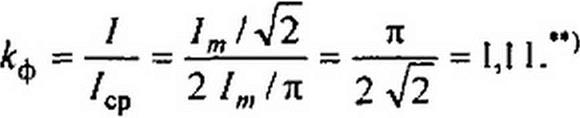 | |||
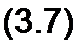 | |||
§ 3.4 Изображение синусоидально изменяющихся величин векторами на комплексной плоскости. Комплексная амплитуда. Комплекс действующего значения. Комплексная плоскость, на которой можно изобразить комплексные числа, дана на рис. 3.2. Комплексное число
имеет действительную (вещественную) и мнимую части. По оси абсцисс комплексной плоскости откладывают действительную часть комплексного числа, а по оси ординат — мнимую часть. На оси действительных значений ставим + I, а на оси мнимых значений + j (у ~ V-T).
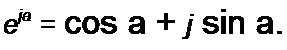 | |||
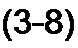 | |||
Из курса математики известна формула Эйлера
Комплексное число е;а изображают на комплексной плоскости вектором, численно равным единице и составляющим угол а с осью вещественных значений (осью + 1). Угол а отсчитываем против часовой стрелки от оси + 1. Модуль функции
| е7 a | = у cos' a + sin2 a = I.
'* Действующее значение измеряют приборами электромагнитной, электродинамической и тепловой систем. Принцип действия измерительных приборов различных систем изучают в курсе электротехнических измерений.
Для несинусоидальных периодических токов * у2. кф х 1.11. Это отклонение косвенно свидетельствует о том. насколько иссииусоидаяьный ток отличается от синусоидального.
Проекция функции еуа на ось + 1 равна cos а, а на ось +у равна sin а. Если вместо функции еуа взять функцию 4е</а» то
4 е; а = lm cos а + j 4 sin а.
Ha комплексной плоскости эта функция, так же как и функция еуа, изображается под углом а к оси + 1, но длина вектора будет в 1т раз больше.
Угол а в формуле (3.8) может быть любым. Положим, что а = со t + ц/, т. е. угол а изменяется прямо пропорционально времени. Тогда
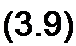 4 е7 (w '+ч/) = Im cos(o) t + у) + j Im sin(w t + ц>).
4 е7 (w '+ч/) = Im cos(o) t + у) + j Im sin(w t + ц>).
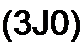 Слагаемое Im cos(w t + ц/) представляет собой действительную часть (Re) выражения 4 ey(w/+v)
Слагаемое Im cos(w t + ц/) представляет собой действительную часть (Re) выражения 4 ey(w/+v)
lm cos(co/ + у) - Re /л/
а функция 4 sin(co t + ц/) есть коэффициент при мнимой части (Im) выражения 4 ey{<1)'+v)
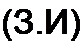 i = /пг sin(co/ + ig) = Im 4 ey(<a'+v).
i = /пг sin(co/ + ig) = Im 4 ey(<a'+v).
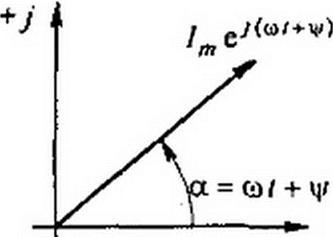
Таким образом, синусоидально изменяющийся ток 7 (ср. (3.1) и (3.11)) можно представить как 1m 4 ey(wf+'|/) или, что то же самое, как проекцию вращающегося вектора 4 ey(“'+v) на ось + j (рис. 3.3).
|
|
Исторически сложилось так, что в радиотехнической литературе за основу обычно принимают не синусоиду, а косинусоиду и потому пользуются формулой (3.10).
С целью единообразия принято на комплексной плоскости изображать векторы синусоидально изменяющихся во времени величин для момента времени w t - 0. При этом вектор
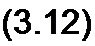 _ > /у _ /
_ > /у _ /
т с ~ 1 т * ~Jni>
где 4— комплексная величина, модуль которой равен /П1; у— угол, под которым вектор 1т проведен к оси + 1 на комплексной плоскости, равный начальной фазе.
Величину 1п, называют комплексной амплитудой тока /. Комплексная амплитуда изображает ток i на комплексной плоскости для момента времени со t = 0. Точка, поставленная над током / или напряжением О, означает, что эта величина во времени изменяется синусоидально.
Поясним сказанное. Пусть ток / - 8 sin(a) t + 20°) А. Запишем выражение для комплексной амплитуды этого тока. В данном случае 1т =8 А, \у = 20в. Следовательно, 4=8еу20°А. Пусть комплексная амплитуда тока 4 = 25 е-'30’ А.
Запишем выражение для мгновенного значения этого тока. Для перехода от комплексной амплитуды к мгновенному значению умножим jm на е70>' и возьмем коэффициент при мнимой части от полученного произведения (см. формулу (3.11)):
i = Im 25 ej 30° е7ш' = Im 25 е’7 (ш /‘30’) = 25 sin(со t ~ 30°).
Под комплексом действующего значения тока или комплексом тока (комплексным током) / понимают частное от деления комплексной амплитуды на 41:
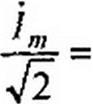 | |||
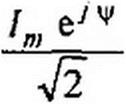 | |||
|
 |
|
Пример 29. Записать выражение комплекса действующего значения тока /т=8е/20А.
Решение. Комплекс действующего значения тока / = 8 е7 :о°/V2 = 5,67 е7 20° А.
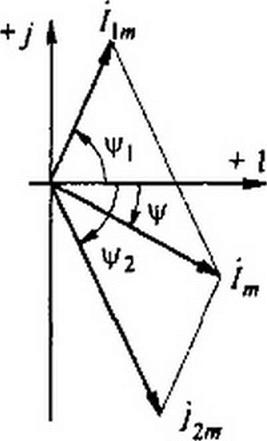
§ 3.5 Сложение и вычитание синусоидальных функций времени на комплексной плоскости. Векторная диаграмма. Положим, что необходимо сложить два тока (/, и /2) одинаковой частоты. Сумма их дает некоторый ток той же частоты:
' = 'i + z2;
/'i = /1л, sin(co t + у/,); /2 = /2ff)sin(oz + y/2);
i = Iт sin(oj t + yr).
Требуется найти амплитуду 1т и начальную фазу у/ тока i. С этой
целью ток изобразим на комплексной плоскости (рис. 3.4) вектором !\т • е' *'. а ток <2 — вектором /. = е7”.
Геометрическая сумма векторов /||н и /2<я даст комплексную амплитуду суммарного тока /д| = [т e7V. Амплитуда тока 1,„ определяется длиной суммарного вектора, а начальная фаза у — углом, образованным этим вектором и осью + 1.
Для определения разности двух токов (ЭДС, напряжений) следует на комплексной плоскости произвести не сложение, а вычитание соответствующих векторов.
Обратим внимание на то, что если бы векторы /)/п, 12т и 1т стали вращаться вокруг начала координат с угловой скоростью о, то взаимное расположение векторов относительно друг друга осталось бы без изменений.
Векторной диаграммой называют совокупность векторов на комплексной плоскости, изображающих синусоидально изменяющиеся функции времени одной и той же частоты и построенных с соблюдением правильной ориентации их относительно друг друга по фазе. Пример векторной диаграммы дан на рис. 3.4.
§ 3.6 Мгновенная мощность. Протекание синусоидальных токов по участкам электрической цепи сопровождается потреблением энергии от источников. Скорость поступления энергии характеризуется мощностью. Под мгновенным значением мощности, или под .мгновенной мощностью, понимают произведение мгновенного значения напряжения и на участке цепи на мгновенное значение тока i, протекающего по этому участку:
P = ui, (3.14)
где р — функция времени.
Перед тем как приступить к изучению основ расчета сложных цепей синусоидального тока, рассмотрим соотношения между токами и напряжениями в простейших цепях, векторные диаграммы для них и кривые мгновенных значений различных величин. Элементами реальных цепей синусоидального тока являются резисторы, индуктивные катушки и конденсаторы. Протеканию синусоидального тока оказывают сопротивление резистивные элементы (резисторы) — в них выделяется энергия в виде теплоты — и реактивные элементы (индуктивные катушки и конденсаторы) — они то запасают энергию в магнитном (электрическом) поле, то отдают ее. Рассмотрим поведение этих элементов.
§ 3.7 Резистивный элемент в цепи синусоидального тока. Как говорилось в § 1.7, резистивный элемент— это идеализированный схемный элемент, учитывающий выделение теплоты в том или ином элементе реальной электрической цепи. Его характеризуют зависимостью напряжения и на нем от протекающего по нему тока i (вольт-амперной характеристикой) или сопротивлением R = и!I. На схемах его изображают, как и резистор, в виде прямоугольника (рис. 3.5, а). Положительные направления отсчета и и i совпадают.
Пусть
i -1„, sinoit.
По закону Ома,
и -iR = R !т sin со/ = Um sin со/; (3.15)
Um = * С
Векторная диаграмма комплекса тока / и совпадающего с ним по фазе комплекса напряжения U показана на рис. 3.5, б.
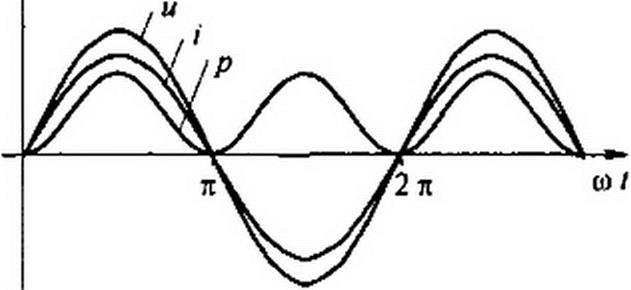
На рис. 3.5, в даны кривые мгновенных значений тока i, напряжения и и мощности

в
Рис. 3.5
Мгновенная мощность р имеет постоянную составляющую ” и Um 2
составляющую —!n^~SL cos2got, изменяющуюся с частотой 2о. Потребляемая от источника питания за время dt энергия равна р dt.
§ 3.8 Индуктивный элемент в цепи синусоидального тока. Индуктивный элемент позволяет учитывать явление наведения ЭДС изменяющимся во времени магнитным потоком и явление накопления энергии в магнитном поле реальных элементов электрической цепи. Его характеризуют зависимостью потокосцепления V оттока i (вебер-амперной характеристикой) или индуктивностью L = ц//Л На электрических схемах индуктивный элемент изображают, как показано на рис. 3.6, а. На схеме замещения реальную индуктивную катушку можно представить в виде последовательно соединенных индуктивного и резистивного элементов.
Выделим индуктивный элемент (рис. 3.6, а). Положительные направления тока i через него, ЭДС самоиндукции eL и напряжение на нем иоЬ указаны на рис. 3.6,'а.
Если / - Im sin со/, то
di
е{ = -L — = -(£> L !т CQStot = w L Im sinfo)l - 90°). dt
Определим разность потенциалов между точками а и Ь. При перемещении от точки b к точке а идем встречно ЭДС е{, поэтому
, di
4>a=4>h~eL И =Va-4>h= ~е!. = L~T
В дальнейшем напряжение на индуктивном элементе будем обозначать uL или, просто, и без индекса
(3.16)
e(* U и
_ 7375^=w L
a L b 1+1
a &L' б
 |
|
Следовательно,
и = со L Im sin(co / + 90°) = (/„, sin(©/+ 90°); Um- со L lm. (3.17)
Произведение со А обозначается X,, называется индуктивным сопротивлением и измеряется в омах (Ом):
X I — со L.
Таким образом, индуктивный элемент (индуктивная катушка, у которой R ~ 0) при синусоидальном токе обладает сопротивлением, модуль которого Xl =&L прямо пропорционален частоте а (см. (3.17)) — на рис. 3.6, б вектор напряжения 0 опережает вектор тока / на 90°. Комплекс ЭДС самоиндукции Ё, находится в противофазе с комплексом напряжения 0.
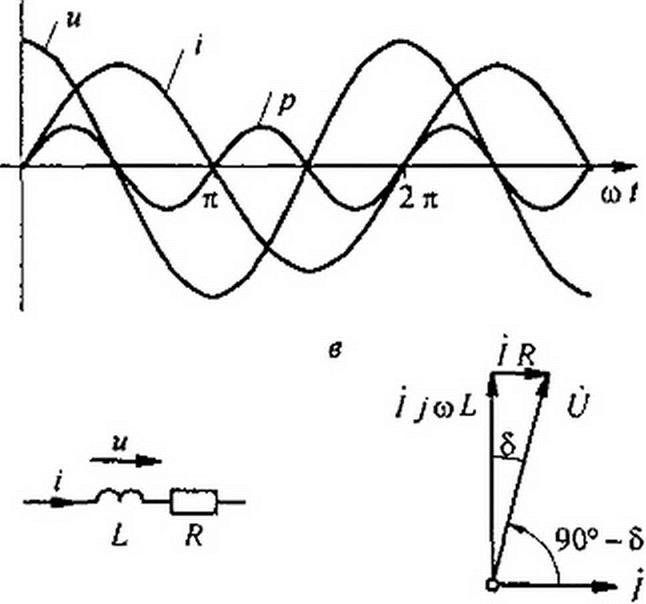
Графики мгновенных значений /, и, р изображены на рис. 3.6, в.
Мгновенная мощность
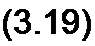 p-ui = U„, cosco/ /п, sin со/ - ^п' sin 2 со z
p-ui = U„, cosco/ /п, sin со/ - ^п' sin 2 со z
проходит через нулевое значение, когда через нуль проходит либо i, либо и. За первую четверть периода, когда и и i положительны, р также положительна. Площадь, ограниченная кривой р и осью абсцисс за это время, представляет собой энергию, которая взята от источника питания на
создание энергии магнитного поля в индуктивной катушке. Во вторую четверть периода, когда ток в цепи уменьшается от максимума до нуля, энергия магнитного поля отдается обратно источнику питания, при этом мгновенная мощность отрицательна. За третью четверть периода у источника снова забирается энергия, за четвертую отдается и т. д. Следовательно, энергия периодически то забирается индуктивной катушкой от источника, то отдается ему обратно.
Падение напряжения на реальной индуктивной катушке равно сумме напряжений на L и на R (рис. 3.6, д). Как видно из этого рисунка, угол между напряжением U на катушке и током / равен 90°-8, причем tg8 == RI&L - \/Qjгде Q{ — добротность реальной индуктивной катушки. Чем больше тем меньше 8.
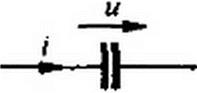
§ 3.9 Емкостный элемент в цепи синусоидального тока. Емкостный элемент — это идеализированный схемный элемент, позволяющий учесть протекание токов смещения и явление накопления энергии в электрическом поле реальных элементов электрической цепи. Его характеризует зависимость заряда q от напряжения и (кулон-вольтная характеристика) или емкость C-q/u. Графическое изображение емкостного элемента такое же, что и изображение конденсатора (рис. 3.7, а). Поло-
 |
|
 |
|
 |
| ||||
| ||||
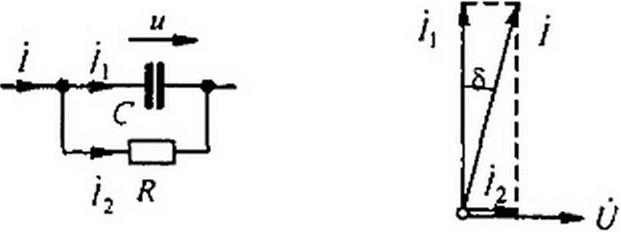 |
| ||||
| ||||
| ||||
жительные направления отсчета и и i совпадают. Если приложенное к конденсатору напряжение и не изменяется во времени, то заряд q = С и на
| одной его обкладке и заряд на другой (С — емкость конденсатора) неизменны, и ток через конденсатор не проходит (/ - dqtdt - 0). Если же напряжение на конденсаторе изменяется во времени, например по синусоидальному закону (рис. 3.7, а): |
| и = U т sin со/, |
| (3.20) |
| то по синусоидальному закону будет меняться и заряд q конденсатора: qС u-С U )U sin со/, т. е. конденсатор будет периодически перезаряжаться. Периодическая перезарядка конденсатора сопровождается протеканием через него зарядного тока: |
| i - ~ - со С Uп, cos оз/ = ■■■-— sin(co / + 90°). dl т 1/wC |
| (3.2J) |
| Из сопоставления (3.20) и (3.21) видно, что ток через конденсатор опережает по фазе напряжение на конденсаторе на 90°. Поэтому на векторной диаграмме (рис. 3.7, б) вектор 1т опережает вектор напряжения на 90°. Амплитуда тока 1М равна амплитуде напряжения Uni, деленной на емкостное сопротивление: |
| (3.22) |
| (3.23) |
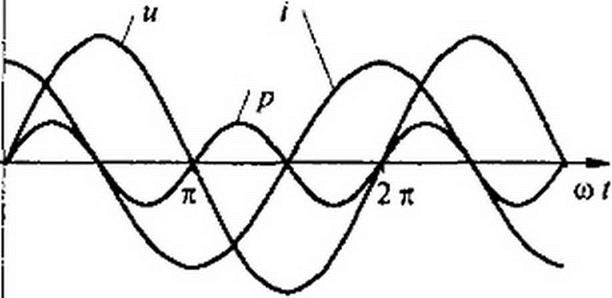
| Емкостное сопротивление обратно пропорционально частоте. Единица емкостного сопротивления — Ом. Графики мгновенных значений w, /, р изображены на рис. 3.7, в. Мгновенная мощность |
| sin 2d)i. |
| (3.24) |
| За первую четверть периода конденсатор потребляет от источника питания энергию, которая идет на создание электрического поля в нем. Во вторую четверть периода напряжение на конденсаторе уменьшается от максимума до нуля, и запасенная в электрическом поле энергия отдается источнику (мгновенная мощность отрицательна). За третью четверть периода энергия снова запасается, за четвертую отдается и т. д. Если проинтегрировать по времени обе части равенства |
| di |
| (3-25) |
| то получим |
| (3.26) |
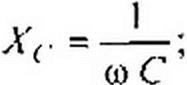
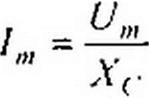
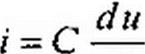
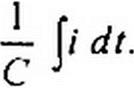
Равенство (3.26) позволяет определить напряжение на конденсаторе через ток по конденсатору. Ток через реальный конденсатор, пластины которого разделены твердым или жидким диэлектриком, в котором имеются тепловые потери, обусловленные вязким трением дипольных молекул и другими причинами, в расчете можно учесть по схеме (рис. 3.7, г). Результирующий ток / = /, + /2.
Ток опережает 0 на 90°, а ток /2 совпадает с U по фазе (рис. 3.7, Э). Угол 8 называют углом п от ерь’. tg8 = I/(?c, где Qc — добротность конденсатора, tg 8 зависит от типа диэлектрика и от частоты и изменяется от нескольких секунд до нескольких градусов.
§ 3.10 
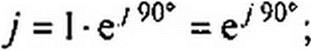
|
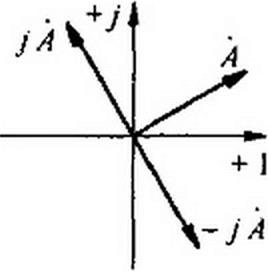
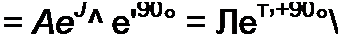 Умножение вектора на у и -у. Пусть есть некоторый вектор А - A (рис. 3.8). Умножение его на у дает вектор, по модулю равный А, но повернутый в сторону опережения (против часовой стрелки), по отношению к исходному вектору А на 90°. Умножение Л на -у поворачивает вектор А на 90° в сторону отставания (по часовой стрелке) также без изменения его модуля. Чтобы убедиться в этом, представим векторы у и -у в показательной форме:
Умножение вектора на у и -у. Пусть есть некоторый вектор А - A (рис. 3.8). Умножение его на у дает вектор, по модулю равный А, но повернутый в сторону опережения (против часовой стрелки), по отношению к исходному вектору А на 90°. Умножение Л на -у поворачивает вектор А на 90° в сторону отставания (по часовой стрелке) также без изменения его модуля. Чтобы убедиться в этом, представим векторы у и -у в показательной форме:
|
(3.27)
(3.28)
(3.29)
-Л у Ле7Ф" е"790° = Ле7(^’9°О). (3.30)
Из (3.29) следует, что вектор у Л, по модулю равный Л, составляет с осью комплексной плоскости угол (ра+ 90°, т. е. повернут против часовой стрелки на 90° по отношению к вектору Л. Согласно (3.30) умножение вектора Л на -у дает вектор, по модулю равный Л, но повернутый по отношению к нему на 90° по часовой стрелке.
§ 3.11 Основы символического метода расчета иепей синусоидального тока. Очень широкое распространение на практике получил символический, или комплексный, метод расчета цепей синусоидального тока.
Сущность символического метода расчета состоит в том, что при синусоидальном токе можно перейти от уравнений, составленных для мгновенных значений и являющихся дифференциальными уравнениями (см., например, (3.31)), к алгебраическим уравнениям, составленным относительно комплексов тока и ЭДС. Этот переход основан на том, что в уравнении, составленном по законам Кирхгофа для установившегося процесса, мгновенное значение тока Z заменяют комплексной амплитудой тока /да; мгновенное значение напряжения на резисторе сопротивлением
| Я, равное Ri—комплексом R по фазе совпадающим с током /т; |
| мгновенное значение напряжения на индуктивной катушке uL комплексом Im j L, опережающим ток на 90°; мгновенное |
| = L — — значение |
| напряжения на конденсаторе ис = |
| i dt— комплексом |
| отстающим от тока на 90°; мгновенное значение ЭДС е — комплек- |
| сом Ет. Справедливость замены и{ - L и 3.10. |
| на / / со L следует из § 3.8 dt |
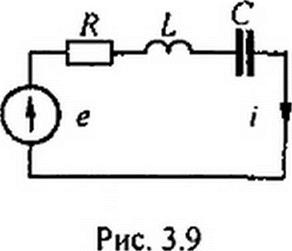
| В § 3.8 было показано, что амплитуда напряжения на L равна произведению амплитуды тока на X L = со £. Множитель j свидетельствует о том, что вектор напряжения на индуктивной катушке опережает вектор тока на 90°. Аналогично, из § 3.9 следует, что амплитуда напряжения на конденсаторе равна амплитуде тока, умноженной на Хс = 1 / © С. Отставание напряжения на конденсаторе от протекающего по ней тока на 90° объясняет наличие множителя - j. Например, для схемы рис. 3.9 уравнение для мгновенных значений можно записать так: |
| ИЛИ |
| di ~dt |
| Запишем его в комплексной форме: |
| /II |
| Вынесем за скобку: |
| (3-32) |
| Следовательно, для схемы рис. 3.9 |
| (3.33) |
| Это уравнение позволяет найти комплексную амплитуду тока /л) через комплексную амплитуду ЭДС Ёт и сопротивления цепи R, со£ и |
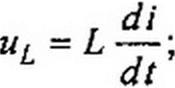
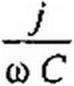
|
Метод называют символическим потому, что токи и напряжения заменяют их комплексными изображениями или символами. Так, R 1т — это изображение или символ падения напряжения i R\ j со L Im— изображение или символ падения напряжения жение или символ падения напряжения на конденсаторе ~ р б/.
§ 3.12 Комплексное сопротивление. Закон Ома для цепи синусоидального тока. Множитель R + j cd L-(j/тС) в уравнении (3.32) представляет собой комплекс, имеет размерность сопротивления и обозначается числом Z. Его называют комплексным сопротивлением'.
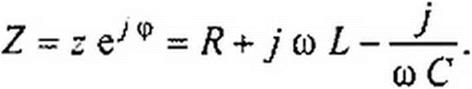 | |||
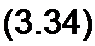 | |||
Как и всякий комплекс, Z можно записать в показательной форме. Модуль комплексного сопротивления принято обозначать через г. Точку над Z не ставят, потому что принято ставить ее только над такими комплексными величинами, которые отображают синусоидальные функции времени.
Уравнение (3.32) можно записать так:
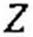 |
Разделим обе его части на 72 и перейдем от комплексных амплитуд 1п) и Ёт к комплексам действующих значений / и Ё:
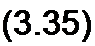 I = EIZ.
I = EIZ.
Уравнение (3.35) представляет собой закон Ома для цепи синусоидального тока.
В общем случае Z имеет некоторую действительную часть R и некоторую мнимую часть j X :
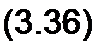 Z = R + j X,
Z = R + j X,
где R — активное сопротивление; X — реактивное сопротивление. Для схемы (рис. 3.9) реактивное сопротивление
X = d)L
§ 3.13 Комплексная проводимость. Под комплексной проводимостью У понимают величину, обратную комплексному сопротивлению Z:
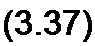 | |||
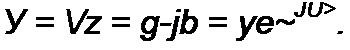 | |||
Единица комплексной проводимости — См (Ом-1). Действительную часть ее обозначают через g, мнимую — через Ь.
Так как
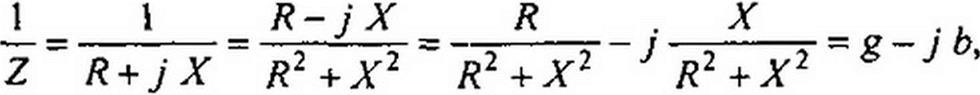 | |||||||||||||||||||||||
 | |||||||||||||||||||||||
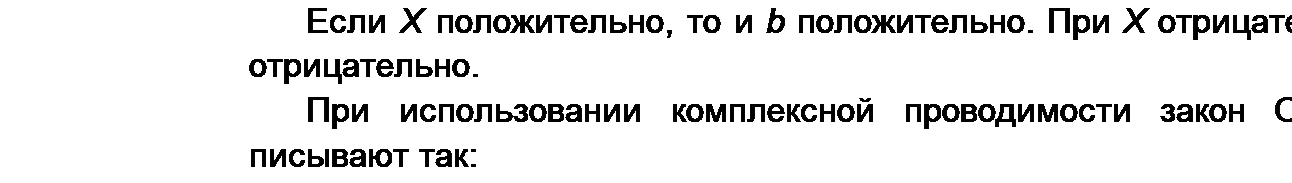 | |||||||||||||||||||||||
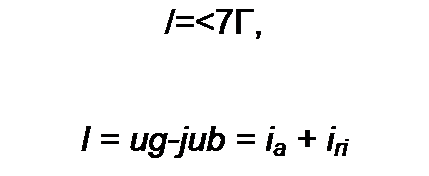 | |||||||||||||||||||||||
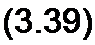 | |||||||||||||||||||||||
 | |||||||||||||||||||||||
 | |||||||||||||||||||||||
 | |||||||||||||||||||||||
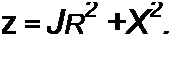 | |||||||||||||||||||||||
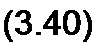 | |||||||||||||||||||||||
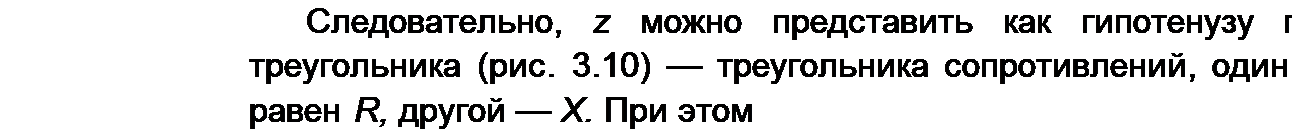 | |||||||||||||||||||||||
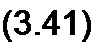 | |||||||||||||||||||||||
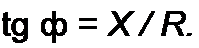 | |||||||||||||||||||||||
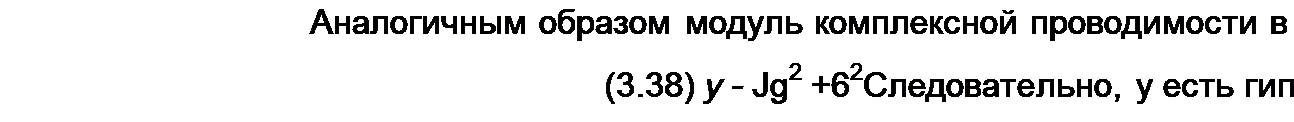 | |||||||||||||||||||||||
 | |||||||||||||||||||||||
|
 |
| ||||
| ||||
 |
§ 3.15 Работа с комплексными числами. При расчете цепей переменного тока приходится иметь дело с комплексными числами: сопротивление участка цепи или цепи в целом — это комплекс, проводимость — комплекс; ток, напряжение, ЭДС — комплексы. Для нахождения тока по закону Ома нужно комплекс ЭДС разделить на комплекс сопротивления.
Из курса математики известно, что комплексное число можно представить в трех формах записи: алгебраической — а + jb, показательной — се7Ч> и тригонометрической— с coscp + y csin<p.
Сложение двух и большего числа комплексов удобнее производить, пользуясь алгебраической формой записи. При этом отдельно складываются их действительные и мнимые части:
(с?! + j Ь\) + (а2 + j Ь2) + (а3 - j b3) = (Qj + а2 + а3) + у (6, + Ь2 - Ь3).
Деление и умножение комплексных чисел целесообразно производить, пользуясь показательной формой записи. Например, нужно разделить комплекс q е7Ф1 на комплекс с2 еr9i. В результате деления будет получен комплекс
г - С| еУФ| -
с2 С2
Модуль результирующего комплекса с3 равен частному от деления q на с2, а аргумент фз - ф] - ф2.
При умножении двух комплексов q e7<?1 и с2 е'ф2 результирующий комплекс
с4 е7^ = q е'ф| с2 е7Ф2 =q с2 е7(ф,+ф2>.
При расчетах электрических цепей часто возникает необходимость в переходе от алгебраической формы записи комплекса к показательной или наоборот
Пусть задано комплексное число a + j b = с е7Ф. Здесь c~\a2+b2-y tg(p = i/a; a = ccos<p; 6 = csinip.
Чтобы не совершить ошибку при записи показательной формы комплекса, рекомендуется сначала качественно изобразить заданный в алгебраической форме комплекс на комплексной плоскости, что позволит правильно выразить угол ф между осью + 1 и вектором. Углы, откладываемые против часовой стрелки от оси + I. считают положительными, по часовой стрелке — отрицательными.
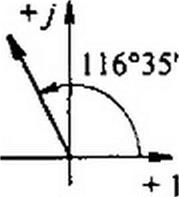
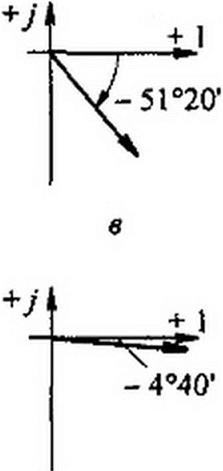
Пример 30. Перевести в показательную форму следующие комплексы: а) 3+2у; б) 2 + Зу; в) 4-5у: г) -6-2у; д) -0.2 + 0,4у; е) 10-у0.8.
Решение пояснено на рис. 3.12. а - е\ а) з + 2 у = Збе'3340• б) 2 + Зу = 3.6е'56^; в) 4-5 у = 6,4 е">51^; г) -6-2у= 6,32 с'7 |6Г25' = 6.32 с'198‘3S'; д) -0,2 + 0,4 у = 0.448 е7’16'35'; е) 10-у0.8 = 10 е*7 4°‘,°'.
§ 3.16 Законы Кирхгофа в символической форме записи. По первому закону Кирхгофа, алгебраическая сумма мгновенных значений токов, сходящихся в любом узле схемы, равна нулю:
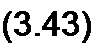 2л=о.
2л=о.
Подставим вместо 1к в (3.43) lk eJ<al и вынеся eJ(al за скобку, получим е7Сй/ = 0. Так как е-/ш/ не равно нулю при любом г, то
(3.44)
Уравнение (3.44) представляет собой первый закон Кирхгофа в символической форме записи.
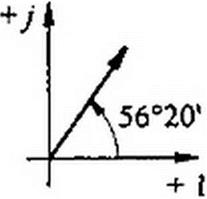 | |||
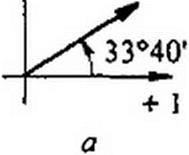 | |||
|
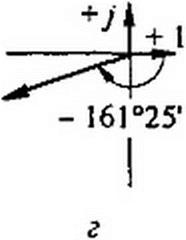 | |||
 | |||
|
 |
Для замкнутого контура сколь угодно сложной электрической цепи синусоидального тока можно составить уравнение по второму закону Кирхгофа для мгновенных значений токов, напряжений и ЭДС.
Пусть замкнутый контур содержит п ветвей и каждая А-ветвь в общем случае включает источник ЭДС ек> резистор Rk, индуктивный Lk и емкостный Ск элементы, по которым протекает ток ik. Тогда, по второму закону Кирхгофа,
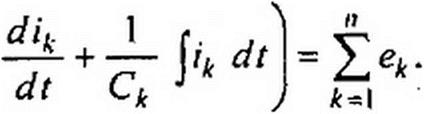 | |||||||
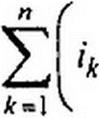 | |||||||
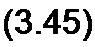 | |||||||
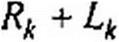 | |||||||
Но каждое слагаемое левой части уравнения в соответствии с § 3.12 можно заменить на 1к 7.к, а каждое слагаемое правой части — на Ек. Поэтому уравнение (3.45) переходит в
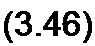 |
п П
к=\ к = 1
Уравнение (3.46) представляет собой второй закон Кирхгофа в символической (комплексной) форме записи.
§ 3.17 Применение к расчету цепей синусоидального тока методов, рассмотренных в главе «Электрические цепи постоянного тока». Для анализа и расчета электрических цепей постоянного тока разработан ряд методов и приемов, облегчающих решение по сравнению с решением системы уравнений при непосредственном использовании законов Кирхгофа. Из гл. 2 известно, что к числу таких методов относятся методы контурных токов, узловых потенциалов, эквивалентного генератора и т. д. Известно также, что окончательные расчетные формулы этих методов получают в результате выводов, в основу которых положены первый и второй законы Кирхгофа.
Поскольку первый и второй законы Кирхгофа справедливы и для цепей синусоидального тока, можно было бы записать уравнения для мгновенных значений величин цепей синусоидального тока, перейти от них к уравнениям в комплексах и затем повторить вывод всех формул гл. 2 для цепей синусоидального тока. Понятно, что проделывать выводы заново нет необходимости.
В том случае, когда отдельные ветви электрической цепи синусоидального тока не связаны между собой магнитно, все расчетные формулы гл. 2 пригодны и для расчета цепей синусоидального тока, если в этих формулах вместо постоянного тока / подставить комплекс тока 7, вместо проводимости g — комплексную проводимость Y, вместо сопротивления R — комплексное сопротивление Z и вместо постоянной ЭДС Е — комплексную ЭДС Ё.
Если же отдельные ветви электрической цепи синусоидального тока связаны друг с другом магнитно (это имеет место при наличии взаимоиндукции), то падение напряжения на каком-либо участке цепи зависит не только от тока данной ветви, но и от токов тех ветвей, с которыми данная ветвь связана магнитно. Расчет электрических цепей синусоидального тока при наличии в них магнитно-связанных ветвей приобретает ряд особенностей, которые не могут быть учтены, если в формулах гл. 2 непосредственно заменить Е на Ё, R на Z и g на Y. Особенности расчета магнитно-связанных цепей рассмотрены в § 3.36.
§ 3.18 Применение векторных диаграмм при расчете электрических цепей синусоидального тока. Ток и напряжения на различных участках электрической цепи синусоидального тока, как правило, по фазе не совпадают. Наглядное представление о фазовом расположении различных векторов дает векторная диаграмма токов и напряжений. Аналитические расчеты электрических цепей синусоидального тока рекомендуется сопровождать построением векторных диаграмм, чтобы иметь возможность качественно контролировать эти расчеты.
Качественный контроль заключается в сравнении направлений различных векторов на комплексной плоскости, которые получают при аналитическом расчете, с направлением этих векторов, исходя из физических соображений. Например, на векторной диаграмме напряжение U, должно опережать ток 7 на 90°, а напряжение Uc — отставать от тока 7 на 90°.
Если аналитический расчет дает результаты, не совпадающие с такими очевидными положениями, то, следовательно, в него вкралась ошибка. Кроме того, векторную диаграмму часто используют и как средство расчета, например в методе пропорциональных величин.
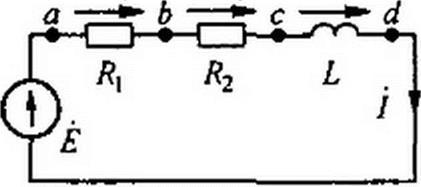
ПримерЗ!. В схеме (рис. 3.13. а) е ~ 141 stnco/ В; /?]=ЗО.ч; /?,=20м;
£ = 0,00955 Гн. Угловая частота (в = 314 рад/с.
Определить ток и напряжение на элементах цепи.
Решение. Запишем уравнение для мгновенных значений
/(??] + R2) + £ — = е.
di
Перейдем от него к уравнению в комплексах:
/ (Л( + /?2) + J (й L / = £ или / Z = £.
где Z = R'+R2+ усо£ = 3 + 2 + /314-0,00955 = 5 + 3/ = 5.82е'31’.
Комплекс действующего значения ЭДС £ = 141/V2 =100 В.
Ток 7 = £/Z = 100/5,8 е7 3|’ = 17.2е’'3,° А.
Напряжения на U = LJal> = 1 Rt = 51,6е“у31 В; на Л2 (J Ri =U - I R2~ В, Hai UL = Ucd =у<о£/=3у-17,2е^эр=51;6е/59в B.
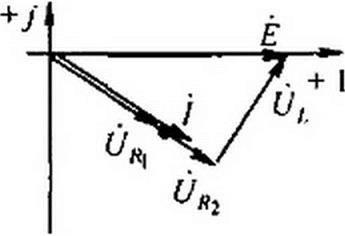
Векторная диаграмма изображена на рис. 3.13, б. Вектор £ направлен по оси + I.
Вектор тока / отстает от него на 31°.
 |
| ||||
| ||||
 |
|
 |
|
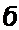 |
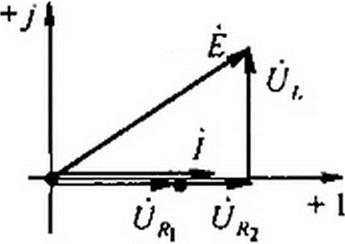
Пример 32. Решить задачу примера 31 методом пропорциональных величин.
Решение. Зададимся током в цепи в 1 А и направим его на векторной диаграмме (рис. 3.13, в) по оси + I (7 = I). Напряжение на R} совпадает по фазе с током и численно раано 1-3 = 3 В. Напряжение на R2 также совпадает с током и равно 2 В. Напряжение на L равно 3 В и опережает ток на 90°. Из прямоугольного треугольника следует, что при токе / = I А на входе £ = ^52 + 32 = 5,82 В. Так как на входе действует ЭДС в 100/5,82 = 17,2 раза больше, то все токи и напряжения должны быть умножены на коэффициент 17,2. На рис. 13.3, в все векторы повернуты на 31е против часовой стрелки по сравнению с соответствующими векторами на рис. 3.13. б. Ясно, что взаимное расположение векторов на диаграмме при этом не изменилось.
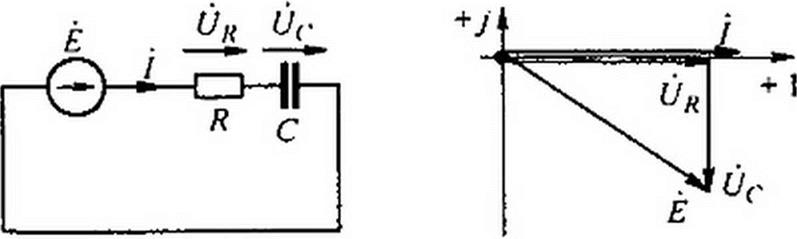
Пример 33. В цели (рис. 3.14, a) R = 4 Ом; о = 105 рад/с. Определить емкость хон* денсатора С, если £ = 10 мВ; / =2 мА.
 |
а б
Рис. 3.14
Решение. Комплексное сопротивление цепи Z^R-jl&C, его модуль •]r2 + (I/соС)2 . По закону Ома 1 = Е/~, отсюда z = у = 10-10"3/2-10”3 = 5Ом. Следовательно, Хс = ]/<оС = 7г2 - £2 = 7э2 - 42 = 3 Ом; С = l/(10s -3) = 3.33 мкФ.
Векторная диаграмма изображена на рис. 3.14, б.
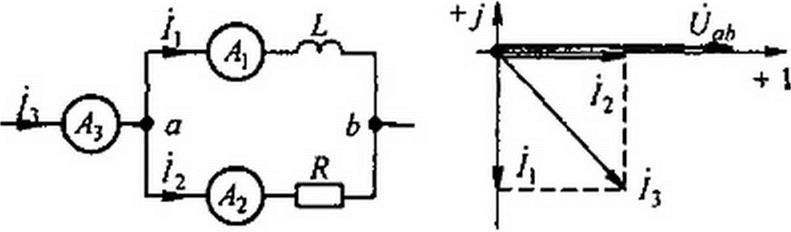
Пример 34. На участке ab разветвленной цепи (рис. 3.15, а) параллельно включены индуктивное X(=aL и активное сопротивление Л, численно равное Х(. Показание амперметра 42=5А. Определить показание амперметра Л3, полагая сопротивления амперметров настолько малыми, что их можно не учитывать.
а б
Рис. 3.15
Решен ие. На рис. 3.15, б качественно построим векторную диаграмму. Напряжение Uah совпадает по фазе с током /2. Ток /, отстает от тока /2 на 90° и равен ему по величине. Ток в неразветвленной части схемы /3 = /( + /2. Модуль тока /3 = 5 >/2 - 7,07 А. Амперметр А^ покажет 7,07 А.
Пример 35. Построить векторную диаграмму токов и напряжений для схемы на рис. 3.16, о, если А=1А, Я| = ЮОм, oL^IOOm, 1/оС = 14,1 Ом, со£3 = 20Ом, /?3 « 2.5 Ом.
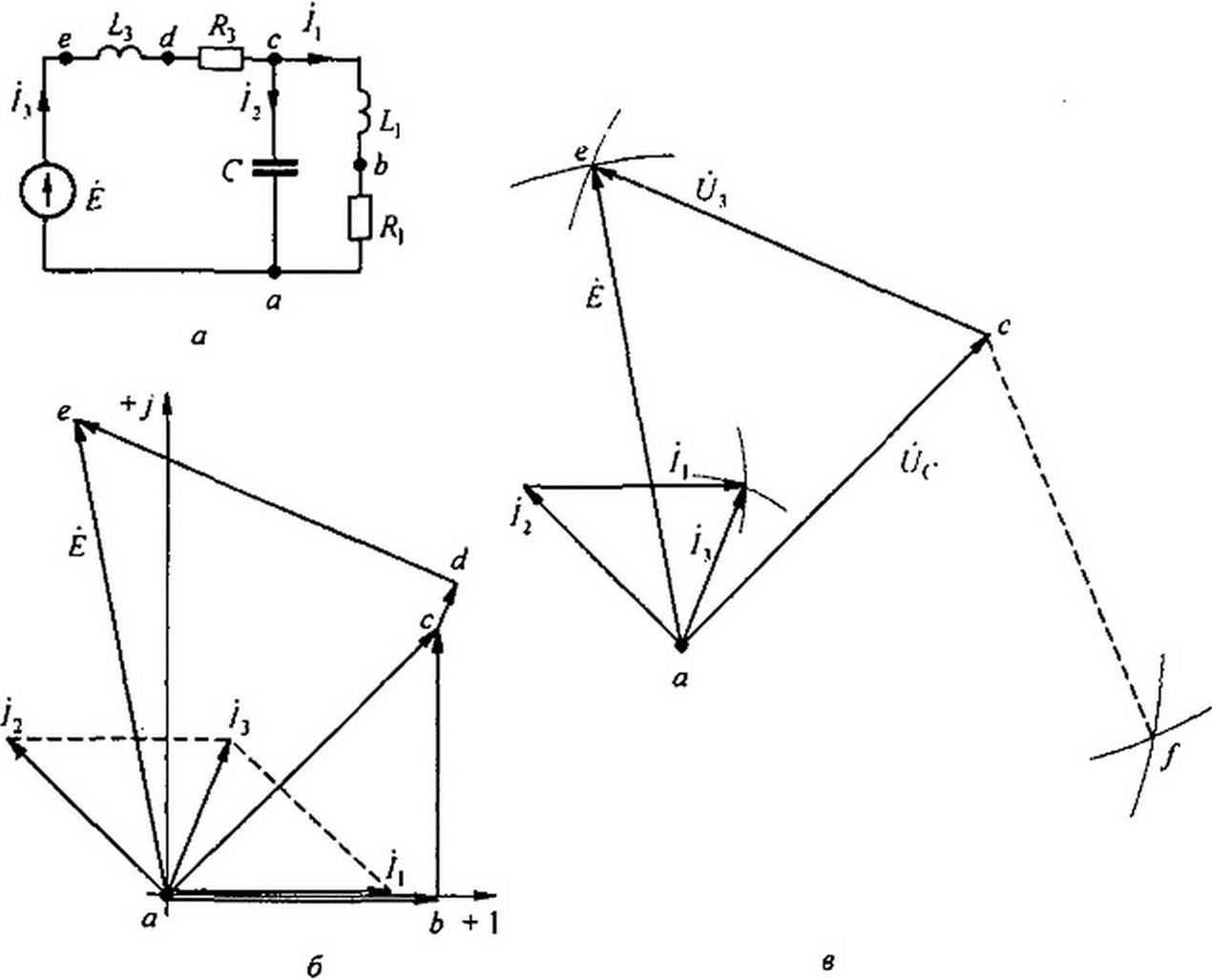
Рис. 3.16
Решение. Обозначим токи и примем положительные направления для них в соответствии с рис. 3.16, а. Выберем масштаб для токов mf = 0,5 А/см и для напряжений mv = 4В/см. Ток / направим по оси + 1 (рис. 3.16, б). Падение напряжения 0^ =10В в по фазе совпадает с током Падение напряжения в индуктивном сопротивлении a>L также равно 10 В, но опережает ток / на 90°. Геометрическая сумма 0^+0ц по модулю равна 10^2 =14,1 В. Емкостный ток /2 опережает это напряжение на 90°. Модуль тока /2 =14,1/14,1 = 1 А. . . .
Ток в неразветвленной части цепи равен геометрической сумме токов: /3 = / + /2. Модуль его равен - 0,8 А (найден графически). Падение напряжения на сопротивлении Я} равно 2 В и совпадает по фазе с током /3. Падение напряжения на индуктивности А) опережает ток 73 на 90° и численно равно 0,8 20 = 16 В. Напряжение на входе схемы равно ЭДС и составляет около 18,3 В.
Пример 36. Решить задачу, обратную рассмотренной в примере 35. В схеме рис. 3.16. а опытным путем найдены значения токов /, /2 и /3 (в ветви схемы включили амперметры и записали их показания), / = I А, /2 = 1 А. /3 = 0,8 А и определены три напряжения: напряжение на входе схемы (У = Е = 18,ЗВ, напряжение на конденсаторе UС = 14,1 В (оно же напряжение на первой ветви) и напряжение на третьей ветви (на Я3 и Ly) Uy *16 В. Напряжения были определены путем подключения вольтметра поочередно к зажимам а и е, а и с, е и с.
По опытным данным (по значениям трех токов и трех напряжений) построить векторную диаграмму.
Решение. На ряс. 3.16, в отложим эехтор (/<-. по модулю равный 14,1 В. Для сопоставления с рис. 3.16, б расположим его на диаграмме так же, как он расположен на рис. 3.16, б.
Изобразим на диаграмме ток /2. Он на 90° опережает напряжение О? и по модулю равен 1 А. После этого построим на диаграмме токи и /3. воспользовавшись тем. что три тока (/,, /2 и /3) образуют замкнутый треугольник (см. рис. 3.16, 5).
Для построения треугольника по трем сторонам (т. е. фактически для определения третьей вершины его) из конца вектора тока (из одной вершины треугольника) проведем дугу радиусом, равным току /(, а из начала вектора тока /, (т. е. из второй вершины треугольника) проводим дугу радиусом, равным току /3.
Точка пересечения этих дуг дает искомую третью вершину треугольника, т. е. точку, в которой оканчиваются векторы токов /3 и После того как на диаграмме определено положение вектора тока /3, можно изобразить на ней векторы напряжения £/3 и ЭДС Ё.
Напряжения 0с, 0у и ЭДС Ё также образуют замкнутый треугольник. Его построение осуществляется аналогично построению треугольников токов.
Из конца вектора 0^ проводим дугу радиусом, равным 03. а из начала вектора 0(— дугу радиусом, равным Е. Дуги пересекаются в точках ей/
Так как напряжение 0 у представляет собой падение напряжения от токд /3 на последовательно соединенных R3 и L3, то оно по фазе должно опережать ток /3, а не отставать от него.
Поэтому из точек е и /выбирают точку е (если бы выбрали точку/ то в этом случае напряжение Оу — штриховая линия на рис. 3.16, в — отставало бы от тока /3, а не опережало его).
В заключение отметим, что в треугольнике токов дуги тоже пересекаются в двух точках. но вторая (лишняя) точка на рис. 3.16. в не показана.
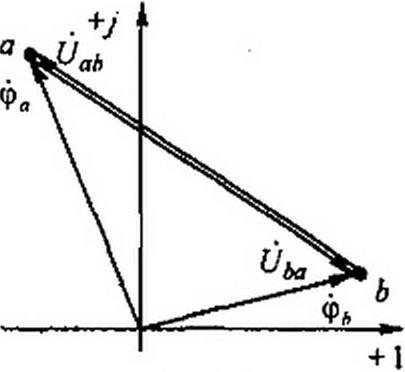
§ 3.19 Изображение разности потенциалов на комплексной плоскости. Потенциалы цепи переменного тока являются комплексными числами. На комплексной плоскости комплексное число можно изображать либо точкой, координаты которой равны действительной и мнимой частям комплексного потенциала, либо вектором, направленным от начала координат к данной точке плоскости.
На рис. 3.17 представлены два вектора, изображающие собой комплексные потенциалы: = -2 + 5 у и = 4 + у.
|
По определению, разность потенциалов йаь =Фа“Фл =-6 + 4 У; иаЬ изобразится вектором, направленным от b к а. Первый индекс у напряжения (в нашем примере индекс а) указывает, к какой точке следует направить стрелку вектора напряжения. Естественно, что йЬа - -0аЬ.
§ 3.20 Топографическая диаграмма. Каждая точка электрической схемы, в которой соединяются элементы схемы, имеет свое значение комплексного потенциала.








