Под методом двух узлов понимают метод расчета электрических цепей, в котором за ис­комое (с его помощью определяют затем токи ветвей) принимают напряжение между двумя узлами схемы.

Дата: 2025-06-02; Просмотры: 13

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Расчетные формулы этого метода получают на основе формул (2.28) и (2.27); их также мож­но просто получить из более общего метода — метода узловых потенциалов (см. § 2.22).

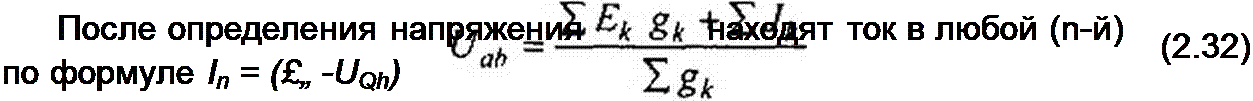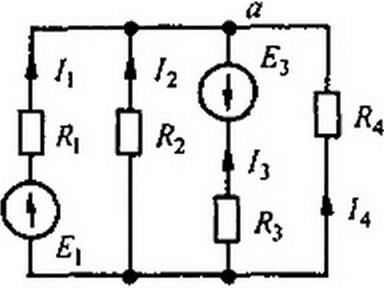
В отличие от схемы на рис. 2.21, а ток / к узлам а и b схемы на рис. 2.23 не подтекает. Поэтому если в формуле (2.28) принять / = 0, то из нее может быть най­дено напряжение между двумя узлами:

Пример 22. Найти токи в схеме на рис. 2.23 и сделать проверку баланса мощности. если£|=120В. £₃ = 5ОВ, Я₍=2Ом. /?₂=40м, Я_} = 1Ом, /?₄=10Ом.

Решение. Определим токи в схеме:

D 120 0.5-50 1 10

°^А 0.5 + 0.25 + 1 + 0,1 1,85 ' '

; £^₌120-ЗЛ ₌ /?1 2

пт 4

/_} = -55,4А; /₄ =-0,54 А.

В схеме потребляется мощность

/,² /?, +/₂² /?₂ + /₃² Я₃ + /₄² =57,3²-2 + 1,35² -4 + 55,4²-1 + 0.54² 10 = 9647Вт.

Источники ЭДС доставляют мощность £] !\ - 1у = 120-57,3+ 50-55,4 = 9647 Вт.

4 2.22. Метод узловых потенциалов. Ток в любой ветви схемы можно найти по закону Ома для участка цепи, содержащего ЭДС. Для того что­бы можно было применить закон Ома, необходимо знать потенциалы узлов схемы. Метод расчета электрических цепей, в котором за неизвест­ные принимают потенциалы узлов схемы, называют методам узловых потенциалов.

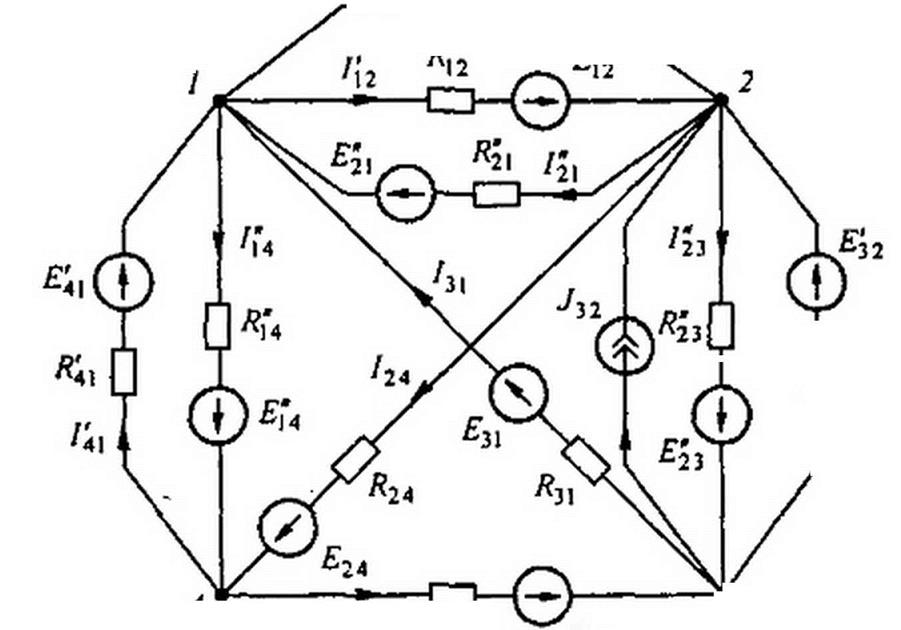^43 /?₄₃ £43

Рис. 2.24

Допустим, что в схеме п узлов. Так как любая (одна) точка схемы может быть заземлена без изменения токораспределения в ней, один из узлов схемы можно мысленно заземлить, т. е. принять потенциал его равным нулю. При этом число неизвестных уменьшается с п до п~ 1.

Число неизвестных в методе узловых потенциалов равно числу урав­нений, которые необходимо составить для схемы по первому закону Кирх­гофа. В том случае, когда число узлов без единицы меньше числа неза­висимых контуров в схеме, данный метод является более экономным, чем метод контурных токов.

Обратимся к схеме (рис. 2.24), которая имеет довольно большое чис­ло ветвей (И) и сравнительно небольшое число узлов (4). Если узел 4 мысленно заземлить, т. е. принять <р₄ =0, то необходимо определить потенциалы только трех узлов: (р,, <р₂» Фз- Для единообразия в обозна­чениях условимся в § 2.22 токи писать с двумя индексами: первый индекс соответствует номеру узла, от которого ток утекает, второй ин­декс — номеру узла, к которому ток подтекает. Проводимости ветвей также будут снабжаться двумя индексами. Необходимо заметить, что эти проводимости не имеют ничего общего с входными и взаимными про­водимостями ветвей, которые рассматривались в § 2.15.

В соответствии с обозначениями токов на рис. 2.24 составим уравне­ние по первому закону Кирхгофа для первого узла:

'41 “'14 ^{+ 1} 2\ “ 42 ⁺ⁱ 2l ⁺ '31 ~

ИЛИ

(^41 “ (Ф1 “Ф4)) #41 “(£|4 “ Сфд “Ф1)) £11 ⁺(0 “(Ф| “ Ф1)) &I2 “
4^12 “(Ф2 -Ф|))£(2 ⁺(^£г’| “Фз» Sl2 ⁺<^£31 “ <Ф| “Фз))£|3 = °-

Перепишем последнее уравнение следующим образом:

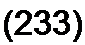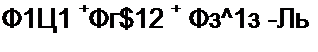ЦI = #41 ⁺ &з ⁺ S\2 ⁺ #41 ⁺ 8\2 + S\i>

Цг = ~(ё]2 ⁺ S\2 + ^Гг)> Цз ~ ~£|з;

Л1 ~ ^41 #41 ⁺ ^31 #31 ⁺ ^21 S2} ~ ^\4 Su ~ Е\₂ ^12-

ПоДОбные же уравнения могут быть записаны и для остальных узлов схемы. Если схема имеет п узлов, то ей соответствует система из п - 1 уравнений:

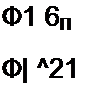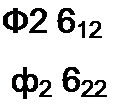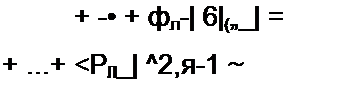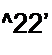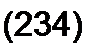Ф1 6_Ч„| ] +ф₂ 6„_| ₂ + ..‘ + ф_л-| 6_Л__} - J_?)_| _я_|.

В общем случае G_kk — сумма проводимостей ветвей, сходящихся в узле к\ G_km — сумма проводимостей ветвей, непосредственно соединяю­щих узлы к и т, взятая со знаком минус. Если между какими-либо дву­мя узлами ветвь отсутствует, то соответствующая проводимость равна нулю. В формировании узлового тока к-узла J_kk участвуют те ветви, под­ходящие к этому узлу, которые содержат источники ЭДС и (или) тока. Если ЭДС Е_р р-ветви направлены к Л-узлу, то ее вклад в формирование J_kk равен Е_р g_py а если эта ЭДС направлена от &-узла, то ее вклад со­ставляет -Е_р g_p. Если к /1-узлу подтекает ток от источника тока, то он должен быть введен в J_kk со знаком плюс, если этот ток от источника тока утекает, то он должен входить в J_kk со знаком минус. После реше­ния системы (234) относительно потенциалов определяют токи в ветвях по закону Ома для участка цепи, содержащего ЭДС.

В том случае, когда в схеме имеются два узла, соединенных ветвью, в которой имеется ЭДС, а сопротивление ее равно нулю, перед состав­лением системы уравнений по методу узловых потенциалов один из этих узлов рекомендуется устранить в соответствии с приемом, рассмотрен­ным в § 2.24.

Система уравнений (234) может быть представлена в матричной фор­ме записи:

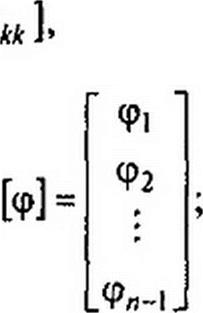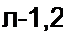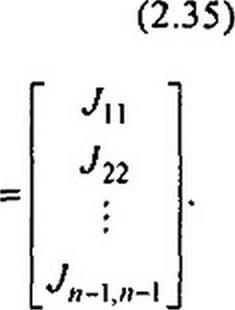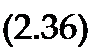[ph [G]-'[J„ ].

Еще Максвеллом было установлено, что распределение токов в электрических цепях всегда происходит так, что тепловая функция системы

^ = ■7- S S ”(ФУ "Фт))² SNm

* W=l.2.3.... «=1,2.3,...

минимальна. Коэффициент 1/2 обусловлен тем, что при двойном суммировании мощность каждой ветви учитывается дважды. Доказательство основано на том, что совокупность уравнений (2.34) является совокупностью условий минимума функций Р, т. е. совокупно­стью условий

JUL₌o. 1-^=о

2 d<Pi 2 Эф₂

и т. д. Так как вторые производные

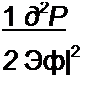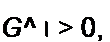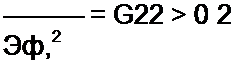положительны, то это и является доказательством минимума тепловой функции Р.

Пример 23. Найти токи в ветвях схемы (рис. 2.24) и сделать проверку по второму закону Кирхгофа. Дано: Е\\ = 10 В; £f₄ = 6 В; Е{₂ = 20 В; Е^=30В; £₃₎ = 14 В; £₂₄ = 10В; £₄₃ = 8 В; £^ = 12 В ; £j₂ = 7B; /?_4| = 1 Ом; /?;₄=2Ом; Л{₂=ЮОм; /?2i — Ю Ом; /?21 ⁼ 5 Ом; /?з| = 2Ом; /?₂₄ = 4 Ом; /?₃₄ = 2 Ом; Р₂₃ ⁼ Ом; Я₃₂ ^а2Ом. Источник тока, включенный между узлами 3 и 2. дает ток J₃₂ ~ 1>$ А.

Решение. Записываем систему уравнений;

( Ф1 $11 ⁺Ф2 $12 ⁺Ф? $13

] Ф1 $21 ⁺ Ф1 $22 ⁺ Ф2 $23 ⁼ *^22 ’
[ ф) $31 + Фэ $32 ⁺ ФЗ $33 ⁼ •бз-

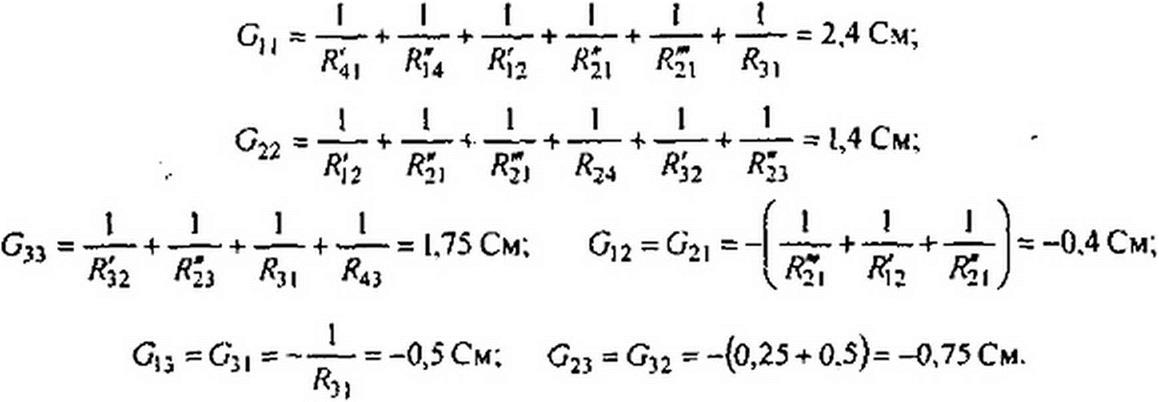При подсчете G,,, G₃₃ и $₂з учтено, что проводимость ветви с источником тока равна нулю (сопротивление источника тока равно бесконечности).

Узловые токи:

j ₊ _^2.₊ ^L₌₁5A;

^{1 1} D* D* D D^f D⁹

Л₄₎ Ky} «21

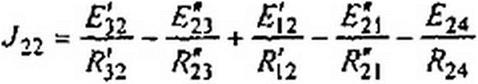=-3.5 +3-7 + 4-1,5 =-5 A.

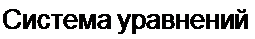2,4 ф) - 0,4 <р₂ " 0.5 ф₃ = 15;

- 0,4 ф] +1,4 ф₂ - 0,75 Фз = -1.5;

- 0,5 ф| - 0,75 ф₂ +1,75 фз = -5

имеет решение ф] = 6 В; ф₂ = 0,06 В; ф₃ = -1,07 В.

Заключительный этап расчета состоит в подсчете токов по закону Ома. Перед опреде­лением токов в ветвях схемы следует эти токи обозначить и выбрать для них положитель­ные направления:

_£;₁-(ф₁-ч>4) ю-(б-о) --------------- j —-4 А.

Л" = ^^Л = -1,185А;

/п = ~ = _{2 у2 А}. ,₄₎₌mL£«₌4.55A.

л₃₂ Я₄з

Сделаем проверку решения по второму закону Кирхгофа для периферийного контура. Алгебраическая сумма падений напряжений 4 • 1 +1,185 • 5 -2,92• 2 - 4,55 • 2 * -5 В.

Алгебраическая сумма ЭДС 10 - 7 - 8 = -5 В.

Покажем, что основная формула (2.32) метода двух узлов получается как частный слу­чай (2.34). Действительно, если один узел схемы (рис. 2.23), например узел Ь, заземлить, то остается найти только один потенциал ф_о =(7_йА. Для получения формулы (2.32) из (2.34) следует положить ф] = ф_Л = U_ah\ ф₂ = ф₃ = ф₄ =... = 0.

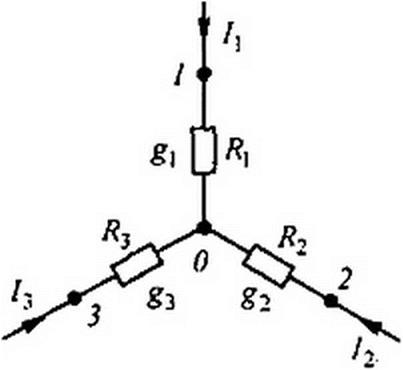
§ 2.23 Преобразование звезды в треугольник и треугольника в звезду. Соединение трех сопротивлений, имеющее вид трехлучевой звез­ды (рис. 2.25), называют звездой, а соединение трех сопротивлений так, что они образуют собой стороны треугольника (рис. 2.26), — треугольником. В узлах /, 2, 3 (потенциалы их ф_ь ф₂ и <р₃) треугольник и звезда соединяются с остальной частью схемы (не показанной на рисунках).

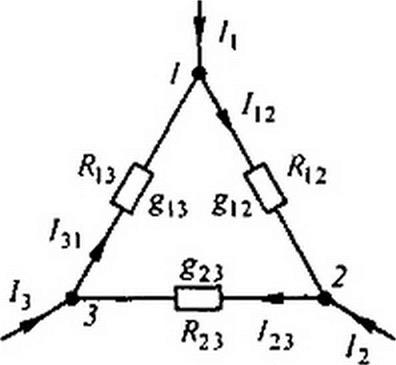
Обозначим токи, подтекающие к узлам Л 2, 3, через /₂ и /₃.

Часто при расчете электрических цепей оказывается полезным пре­образовать треугольник в звезду или. наоборот, звезду в треугольник. Практически чаще бывает необходимо преобразовать треугольник в звез­ду. Если преобразование выполнить таким образом, что при одинаковых значениях потенциалов одноименных точек треугольника и звезды под­текающие к этим точкам токи одинаковы, то вся внешняя схема «не за­метит» произведенной замены.

Выведем формулы преобразований, С этой целью выразим токи /_}, /₂ и /₃ в звезде и в треугольнике через разности потенциалов точек и соответствующие проводимости.

Для звезды

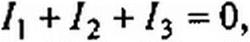
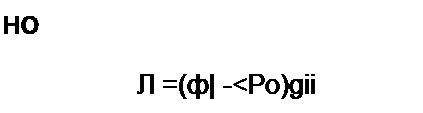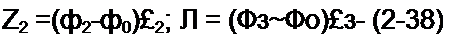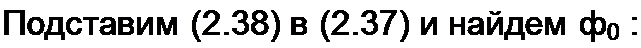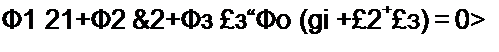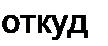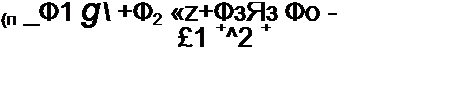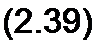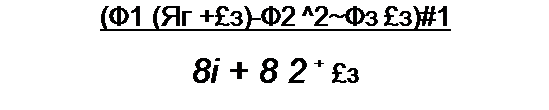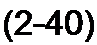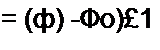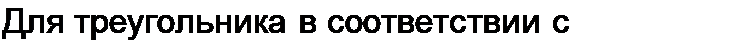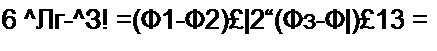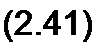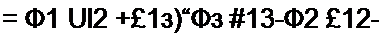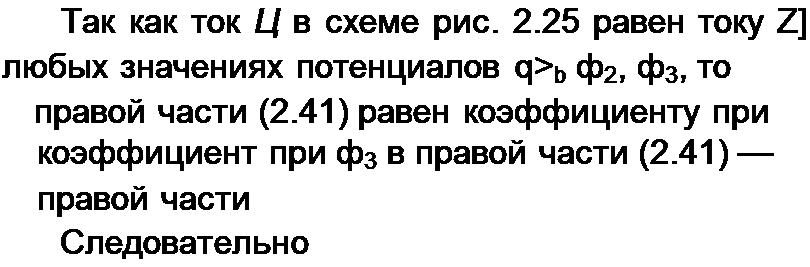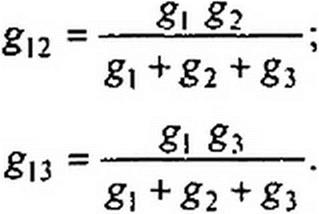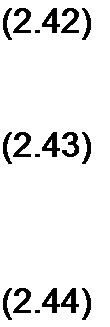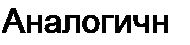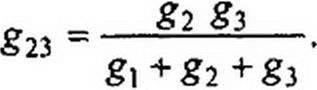(2.37)

Из уравнений (2.42)-(2.44) выразим сопротивления лучей звезды R_} = 1/gp R₂ = 1/&2 ^и R3 8з через сопротивления сторон треуголь­ника: /?_|2=I/g_I2; Д₂₃=1/£₂₃; /?₁₃ =l/g_J3.

С этой целью запишем дроби, обратные (2.42)-(2.44):

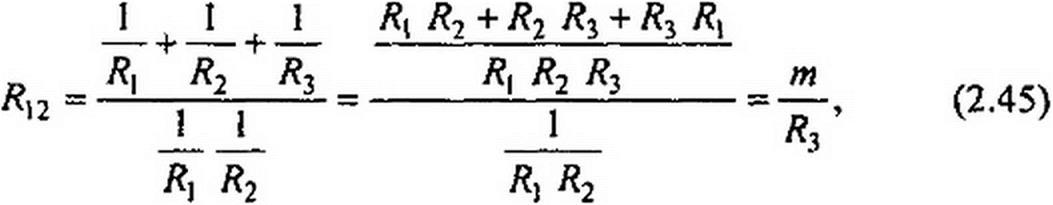где

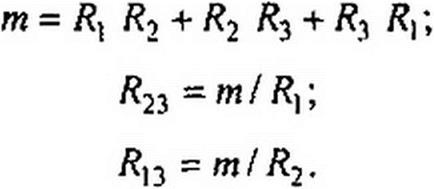(2.46)

(2-47)

(2-48)

Подставив (2.45), (2.47) и (2.48) в (2.46), получим

2^1 1 1 2 #12 #23 #13

т = т ------------- +----------- +----------- ~т —---------------------- —---------- —.

\ #23 #13 #13 #12 R]2 #23 J #12 #23 #13

Следовательно,

#12 #23 #.3

#12 ⁺ #23 ⁺ #13

Подставив т в (2.47), найдем

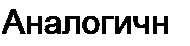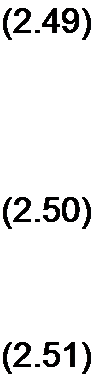#12 7?|з

#23 #12

#12 ⁺ #23 ⁺ #13

#13 ^23

#12 ⁺ #23 ⁺ #13

Структура формул (2.49)-(2.51) аналогична структуре формул (2.42)-(2.44).

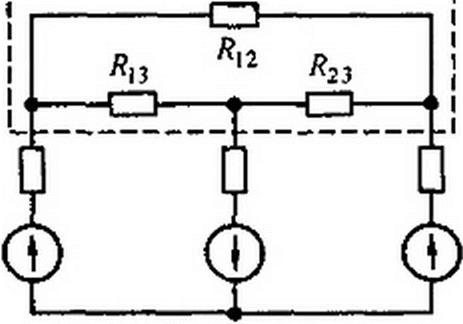
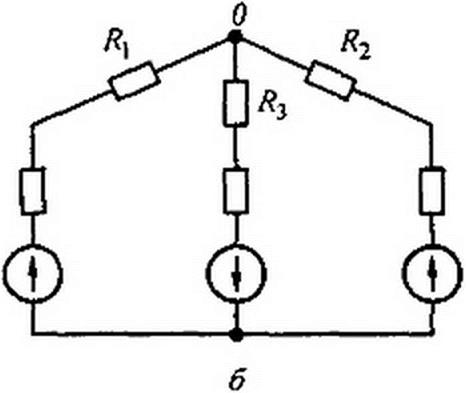
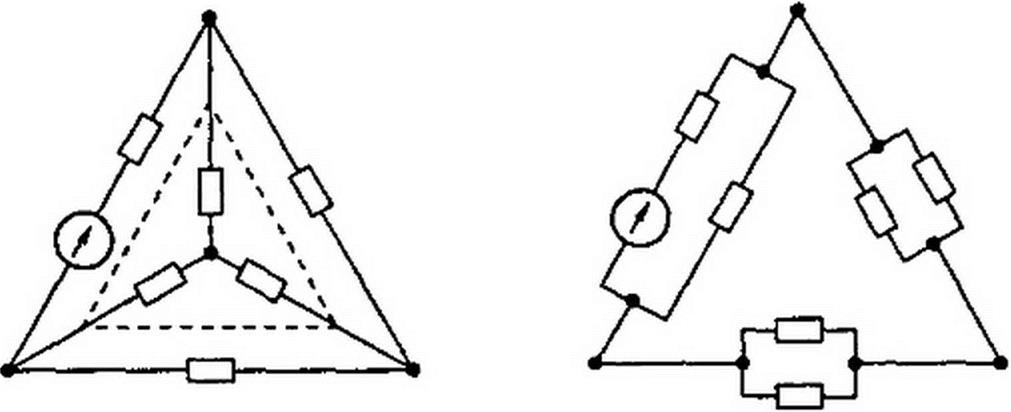
Преобразование треугольника в звезду можно пояснить, рассмотрев, например, рис. 2.27, а, б. Схема до преобразования изображена на рис. 2.27, а_у штриховой линией обведен преобразуемый треугольник. На рис. 2.27, б представлена та же схема после преобразования. Расчет то­ков произвести для нее проще (например, методом двух узлов), чем для схемы на рис. 2.27, а.

В полезности преобразования звезды в треугольник можно убедить­ся на примере рис. 2.27, в, г. Схема до преобразования изображена на рис. 2.27, в, штриховой линией обведена преобразуемая в треугольник звезда. На рис. 2.27, г представлена схема после преобразования, кото­рая свелась к последовательному соединению сопротивлений’¹.

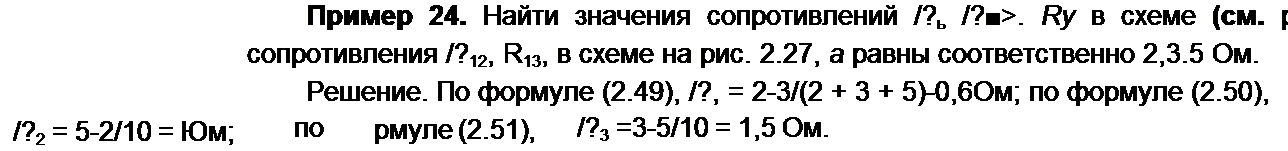§ 2.24 Перенос источников ЭДС и источников тока. На участке цепи рис. 2.28, а между узлами а и b имеется источник ЭДС £. Этот ис­точник можно перенести в ветви 1 и 2, а узел а устранить и в результате получить участок на рис. 2.28, б. Эквивалентный переход поясняется рис. 2.28, в. Точки с, d, b имеют одинаковый потенциал и потому могут быть объединены в одну точку Ь.

Участок abc на рис. 2.28, г, между крайними точками а и с которого включен источник тока, может быть заменен участком рис. 2.28, б, отли­чающимся от участка рис. 2.28, г тем, что источник тока между точками а и с заменен на два источника, присоединенных параллельно 2?_{ и /?₂- Эквивалентность замены следует из неизменности значений токов в каж­дом из узлов. Ток в узле b не изменился, так как в этот узел добавили и

*’ В §3.31 рассмотрен сше один вил преобразований — преобразование последова­тельно-параллельного соединения в параллельное.

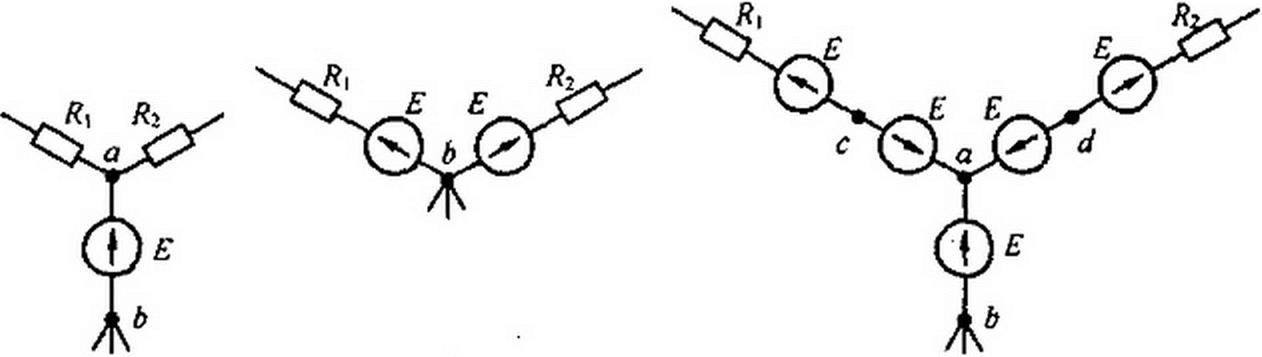
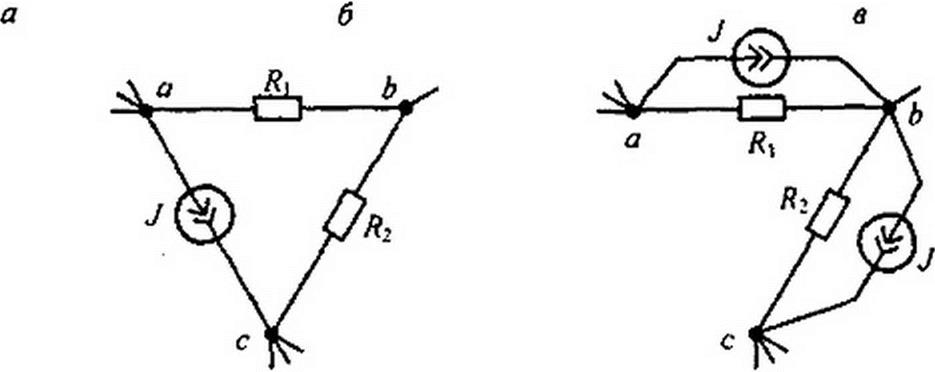
г д

Рис. 2.28

вычли ток J. Практически источники переносят при преобразованиях схем с целью их упрощения и при записи уравнений по методу контур­ных токов и узловых потенциалов в матрично-топологической форме записи (см. § 2.33).

§ 2.25. Активный и пассивный двухполюсники. В любой электри­ческой схеме можно мысленно выделить какую-то одну ветвь, а всю ос­тальную часть схемы независимо от ее структуры и сложности условно изобразить некоторым прямоугольником (рис. 2.29, а). Такой прием был

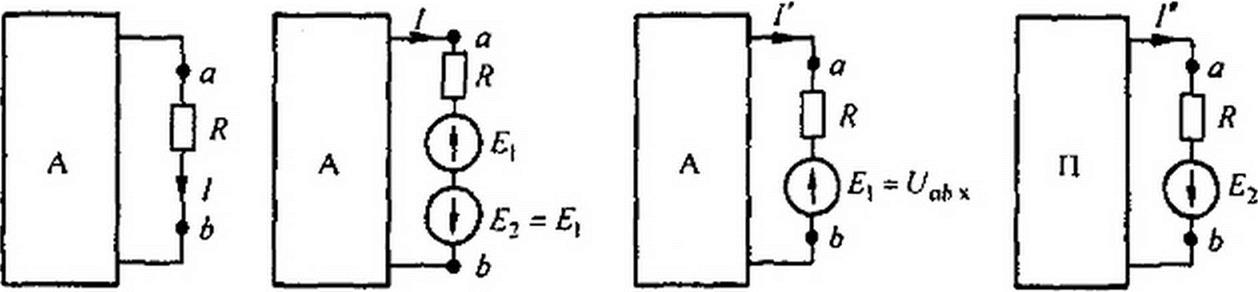
а б в г

Рис. 2.29

использован в § 2.17 без специальных объяснений. По отношению к выделенной ветви вся схема, обозначенная прямоугольником, представ­ляет собой так называемый двухполюсник.

Таким образом, двухполюсник — это обобщенное название схемы, которая двумя выходными зажимами (полюсами) присоединена к выде­ленной ветви.

Если в двухполюснике есть источник ЭДС или (и) тока, то такой двух­полюсник называют активным. В этом случае в прямоугольнике ставят букву А (рис. 2.29, а-в).

Если в двухполюснике нет источника ЭДС и (или) тока, то его на­зывают пассивным. В этом случае в прямоугольнике либо не ставят никакой буквы, либо ставят букву П (рис. 2.29, г).

§ 2,26, Метод эквивалентного генератора. По отношению к вы­деленной ветви двухполюсник можно заменить эквивалентным генера­тором, ЭДС которого равна напряжению холостого хода на зажимах выделенной ветви, а внутреннее сопротивление равно входному сопро­тивлению двухполюсника.

Пусть задана некоторая схема и требуется найти ток в одной ее вет­ви. Мысленно заключим всю схему, содержащую ЭДС и сопротивления, в прямоугольник, выделив из нее ветвь ab, в которой требуется найти ток I (рис. 2.29, а).

Ток I не изменится, если в ветвь ab включить две равные и противо­положно направленные ЭДС £] и £₂ (^см- Р^ис- 2.29, 6).

На основании принципа наложения ток можно представить в виде суммы двух токов — Г и Г: / = /' + /*.

Под током Г будем понимать ток, вызванный источником ЭДС Е_} и всеми источниками ЭДС и тока активного двухполюсника, заключенны­ми в прямоугольник. Ток Г вызывается только одним источником ЭДС £₂. В соответствии с этим для нахождения токов Г и Г используем рис. 2.29, в, г. В прямоугольнике П (рис. 2.29, г) отсутствуют все источ­ники, но оставлены их внутренние сопротивления.

ЭДС Е_{ направлена встречно напряжению U_ah. По закону Ома для участка цепи, содержащего ЭДС,

/■ = У ^£1. (2.52)

Выберем £| так, чтобы ток /' был равен нулю. Отсутствие тока в ветви ab эквивалентно ее размыканию (холостому ходу). Напряжение на зажимах ab при холостом ходе ветви обозначим

Следовательно, если выбрать £| -U_ahxy то /' = 0. Так как / = /'+/*, а /' = 0, то / = /’. Но ток /’ в соответствии со схемой (см. рис. 2.29, г) определяется так:

/' = —^2— = (2 53)

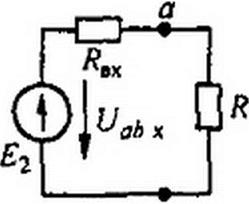
где £_вх — входное сопротивление двухполюсника по отношению к зажи­мам ab, R — сопротивление ветви ab. Уравнению (2.53) отвечает экви­валентная схема на рис. 2.30, а, где вместо двухполюсника изображены источник ЭДС U_af)X = Е₂ и сопротивление /?_вч (схема Гельмгольца— Тевенена).

Совокупность источника ЭДС ^2⁼^ahx и сопротивления R_BX мож­но рассматривать как некоторый эквивалентный генератор (Л_вх являет­ся его внутренним сопротивлением, a U_abx — его ЭДС).

Таким образом, по отношению к выделенной ветви (ветви ab на рис. 2.29, а) всю остальную часть схемы можно заменить эквивалентным генератором с перечисленными значениями параметров.

Метод расчета тока в выделенной ветви, основанный на замене ак­тивного двухполюсника эквивалентным генератором, принято называть .методом эквивалентного генератора (активного двухполюсника), а так­же методом холостого хода и короткого замыкания.

В дальнейшем чаще используется первое название.

Рекомендуется такая последовательность расчета тока этим методом: а) найти напряжение на зажимах разомкнутой ветви ab\

б) определить входное сопротивление Я_вх всей схемы по отношению к зажимам ab при закороченных источниках ЭДС и разомкнутых ветвях с источниками тока’’;

в) подсчитать ток по формуле

(2.54)

Если сопротивление ветви ab равно нулю R = 0, то для нее имеет место режим короткого замыкания, а протекающий по ней ток есть ток короткого замыкания (/_к). Из (2.54) при R = 0

_х / R_BX,

^вх

Из формулы (2.56) следует простой метод опытного определения вход­ного сопротивления активного двухполюсника. Для этого необходимо измерить напряжение холостого хода на зажимах разомкнутой ветви U_ah* и ток короткого замыкания /_к ветви, а затем найти /?_вх как част­ное от деления U_abx на /_и.

“'Если среди источников литания схемы есть источники тока, то при определении вход­ного сопротивления всей схемы по отношению к зажимам ab ветви с источниками тока следует считать разомкнутыми. Это станет понятным, если вспомнить, что внутреннее сопротивление источников тока равно бесконечности (см. § 2.2).

Название метода — метод холостого хода и короткого замыкания — объясняется тем, что при решении этим методом для нахождения ^_а/>х используется холостой ход ветви ab, а для определения входного сопро­тивления двухполюсника R** — короткое замыкание ветви ab.

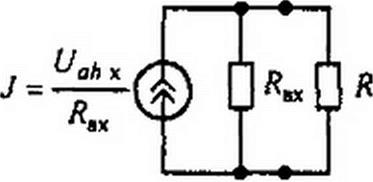
Заменив источник ЭДС источником тока, получим схему эквивалент­ного генератора (рис. 2.30, б).

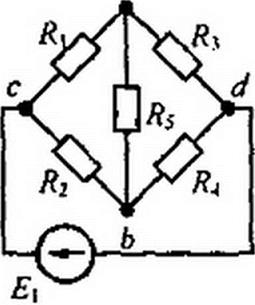
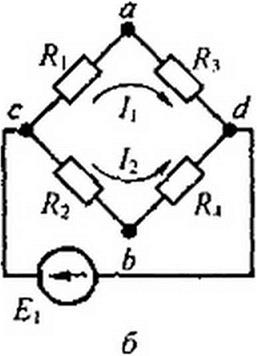
Пример 25. Определить ток в диагонали ab мостовой схемы рис. 2.31, а, полагая Я^/^-НОм; Л₂ = 40м; /?₃ = 20м; /?₅ = 2Ом £_{1 =} 10В.

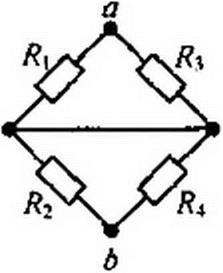Решение. Размыкаем ветвь ab (рис. 2.3U о) и находим напряжение холостого хода:

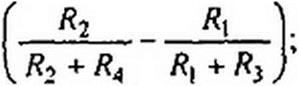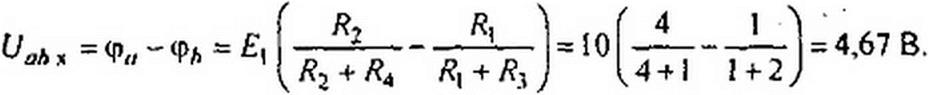/?[ /?- /?7 ^4 1'2 4 1 , _ _

= —!—— + —=--------------------------------------- +--------------------------------------- = 1.47 Ом.

⁸⁴ /?,+ /?₅ /fj +/?д 1 + 2 4 + 1

Определяем ток в ветви по формуле (2.54):

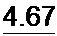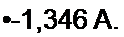§ 2.27 Передача энергии от активного двухполюсника нагрузке. Если нагрузка R подключена к активному двухполюснику' (рис. 2.29, а), то через нее потечет ток / = U_ahx /(R+ R_ax) ив ней выделится мощность

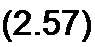P=±Z²/?~- ------- /?.
(/? + /?_вх )²

Выясним, каково должно быть соотношение между сопротивлением нагрузки R и входным сопротивлением двухполюсника Я_вх> чтобы в со­противлении нагрузки выделялась максимальная мощность; чему она

равна и каков при этом КПД передачи. С этой целью определим первую производную Р по R и приравняем ее к нулю:

dR </?+£„)“

Отсюда

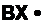(2.58)

Нетрудно найти вторую производную и убедиться в том, что она от­рицательна (d²?/d/?² <0). Следовательно, соотношение (2.58) соответ­ствует максимуму функции Р =f(R). Подставив (2.58) в (2.57), получим максимальную мощность, которая может быть выделена в нагрузке Л:

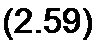> 14 R .

max ab х ' *вх *

Полезную мощность, выделяющуюся в нагрузке, определяют по урав­нению (2.57). Полная мощность, выделяемая эквивалентным генератором,

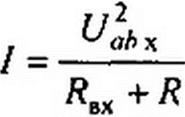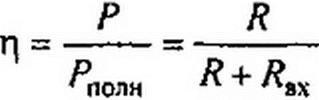Коэффициент полезного действия

(2.60)

Если R = Я_вх, то л - 0,5.

Если мощность Р значительна, то работать с таким низким КПД, как 0,5, недопустимо. Но если мощность Р мала и составляет всего несколь­ко милливатт (такой мощностью обладают, например, различные датчи­ки устройств автоматики), то с низким КПД можно не считаться, посколь­ку достигнута главная цель — в этом режиме датчик отдает нагрузке максимально возможную мощность. Выбор сопротивления нагрузки R, равного входному сопротивлению /?_вх активного двухполюсника, назы­вают согласованием нагрузки.

Пример 26. При каком значении сопротивления /?$ (рис. 2.31, а) в нем выделяется максимальная мощность и чему она равна?

Решение. Из условия (2.58) находим

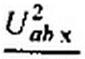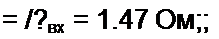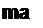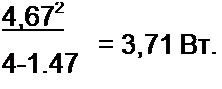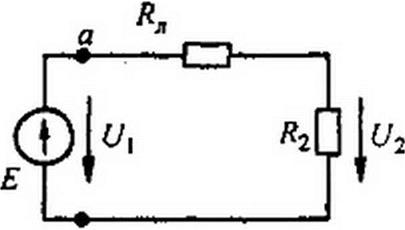
§ 2.28 Передача энергии по линии передачи. Схема линии переда­чи электрической энергии изображена на рис. 2.32, где (7, — напряже­ние генератора в начале линии; U₂ — напряжение на нагрузке в конце
линии; /?_л— сопротивление проводов линии; R₂— сопротивление на­грузки.

Напряжение U\=U_ab (рис. 2.32) направлено про­тивоположно ЭДС Е. Объясняется это тем, что напряже­ние имеет направление от точки с более высоким потенциалом к точке с более низким, тогда как ЭДС направлена от точки с более низким потенциалом к точ­ке с более высоким, т. е. стрелка внутри источника ЭДС указывает направление возрастания потенциала внутри источника.

Рис. 2.32 При передаче больших мощностей (напри­

мер, нескольких десятков мегаватт) в реаль­ных линиях передач КПД п = 0,94 4- 0,99, а напряжение U₂ лишь на не­сколько процентов меньше U_}. Ясно, что каждый процент повышения КПД при передаче больших мощностей имеет существенное экономичес­кое значение.

Характер изменения мощности в начале линии мощности в нагрузке Р₂, КПД Т| и напряжения на нагрузке U₂ ^в функции от тока по линии при С/, = const, R_n - const иллюстрируется кривыми на рис. 2.33, а. По оси абсцисс отложен ток /, по оси ординат — P₂,U₂,^\-

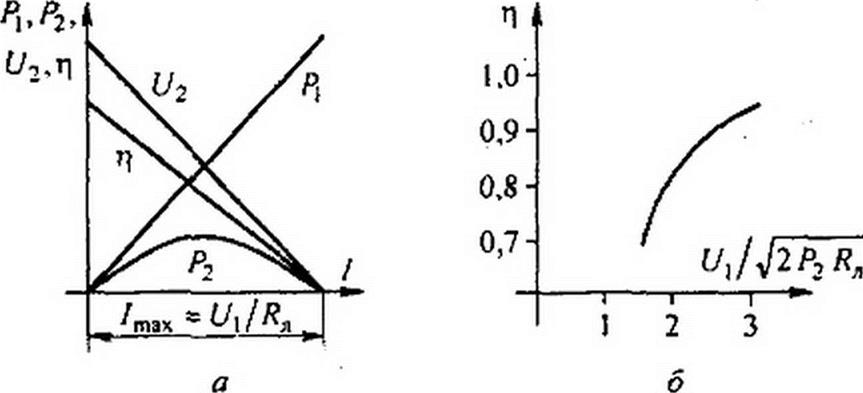Максимальное значение тока /_1пах = Ц / R_n имеет место при коротком замыкании нагрузки. Кривые построены по уравнениям

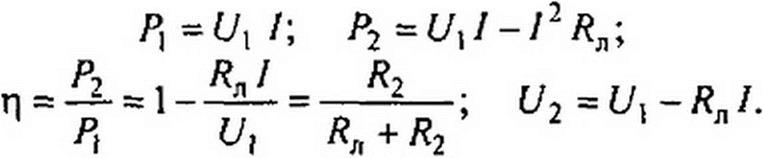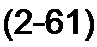Если по линии передачи с сопротивлением R_n и сопротивлением на­грузки R₂ должна быть передана мощность

(2.62)

то КПД передачи тем выше, чем выше напряжение Ц в начале линии.

Пример 27. Вывести формулу, показывающую, как при заданных Р₂ и R_n КПД за­висит от напряжения в начале линии.

Решение, Из (2.62) определим Я₂ = Р₂ / /². Так как / - Uy + Я₂), то

(2.63)

Решим уравнение (2.63) относительно R₂ (знак минус в формуле (2.64) перед корнем

отброшен, так как он соответствует правой части кривой Р₂ = /(/) с меньшим п):

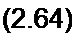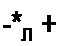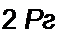Таким образом,

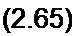Л₂ /?₂+Я_л-/?_л ।

/?„ + R-, R„ + R->

Р₂Рл '

На рис. 2.33, б изображена зависимость п = f^t^,^P₂R_fl), построенная по форму­ле (2.65). Из рисунка видно, что И возрастает с увеличением Ц.

§ 2.29 Некоторые выводы по методам расчета электрических цепей.

1. Наиболее эффективными являются метод узловых потенциалов (МУП) и метод контурных токов (МКТ).

2. Методика составления уравнений этими методами, рассмотренная в § 2.13 и 2.22, проста, упорядочена и позволяет легко контролировать правильность подсчета коэффициентов левой и правой частей уравнений непосредственно по схеме.

3. Системы уравнений МУП и МКТ решают обычно с помощью мик­рокалькулятора, а относительно сложные схемы рассчитывают на ком­пьютере.

4. Уравнения теории цепей могут быть составлены и матрично-топо- логическим методом, использующим некоторые топологические понятия и соответствующие им матрицы. Рассмотрим, как это делается. Но сна­чала напомним некоторые сведения о матрицах.

230. 230. Основные свойства матриц и простейшие операции с ними. Матрица — это совокупность чисел, расположенных в виде прямоугольной таблицы. Чтобы отличать матрицу по внешнему виду от определителя, ее заключают в квадратные скобки. Каждый элемент матрицы снабжают двумя индексами: первый соответствует номеру строки, вто­рой — номеру столбца.

Матрицу называют квадратной, если число строк в ней равно числу столбцов

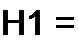
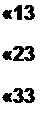«II «12

^а1\ ^агг

<*31 «31

Диагональной называют матрицу, у которой элементы главной диагонали не равны нулю, а все остальные — нули, например:

°ll ⁰

О a₂₂

Матрицу, у которой элементы главной диагонали равны единице, а все остальные — нули, называют единичной-.

I О О'

[1]= 0 1 О

Неопределенной называют матрицу, у которой сумма элементов любой строки и лю­

бого столбца равна нулю.

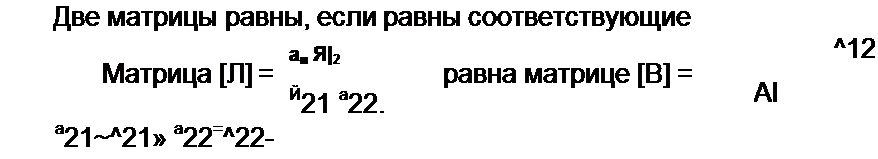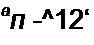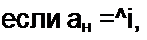У равных матриц равны определители. В рассматриваемом примере а_} ] а₂₂ “ °i2 °2i = = 5ц b22 ~^i2 ^21 > ^{ио из} равенства двух определителей еще не следует равенства самих матриц. Операции над матрицами (их сложение, умножение) постулированы из соображе­ний рациональности. При сложении (вычитании) матриц следует сложить (вычесть) соот­

ветствующие элементы этих матриц:

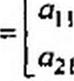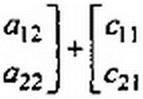При умножении двух матриц (число столбцов первой должно быть равно числу строк второй) т-ю строку первой матрицы умножают на А-й столбец второй. Умножим две мат­рицы, элементами которых являются числа

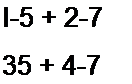1-6 + 2-8

3-6 + 4-8 ‘

А

Руководствуясь приведенным правилом, нетрудно убедиться в том, что

т. е. результирующая матрица зависит от последовательности расположения матриц сомно­жителей. По отношению к матрице (Л), когда ее определитель не равен нулю, можно со­ставить обратную матрицу (Л]"'. Для этого необходимо:

а) каждый элемент исходной матрицы [Л] заменить его алгебраическим дополнением;

б) транспонировать полученную матрицу, т. е. строки сделать столбцами;

в) разделить полученную матрицу на определитель исходной матрицы [Л].

Пример 28. Составить [Л]"¹ для [Л] =

L°2I °22.

Решение. Заменив элементы на алгебраические дополнения, получим матрицу

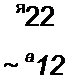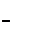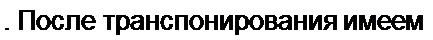^22 ~^12

CJ» 1 ^22 ~ ^12 ^21

Произведение [Я] [Л]"¹ =[1].

Для решения уравнения [Л][23] = [С] относительно матрицы [5] следует обе части этого уравнения умножить на [Л]”¹: (Я)'¹[Я](61 = (Л)'¹ (С) и учесть, что [Л]'¹ [Л] =[!].

В результате получим

[5] = Н]-'[С].

В матричном уравнении можно переставлять столбцы в матрице [Л] при

одновременной перестановке строк в матрице [Z].

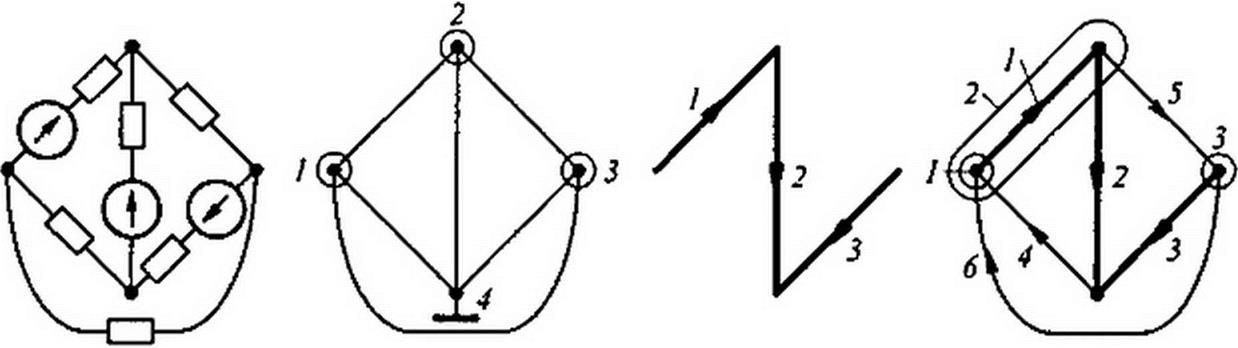
§ 2.31 Некоторые топологические понятия и топологические матрицы. Положим, что в схеме имеется у.узлов, в ветвей и каждая пара узлов соединена одной ветвью. Если в исходной схеме между каким-то двумя узлами имеется несколько параллельных ветвей, то их следует заменить одной эквивалентной. Перед составлением топологических мат­риц ветви схемы (графа) нумеруют и ставят стрелки, указывающие положительные направления для отсчета тока и напряжения на каждой ветви. Перед нумераций ветвей графа нужно выбрать дерево. Как ука­зывалось в § 2.8, дерево представляет такую совокупность узлов схемы и соединяющих их ветвей, когда ветви касаются всех узлов, но не образуют

а б в

Рис. 2.34

ни одного замкнутого контура. Число ветвей дерева равно (у - 1). Нуме­рацию ветвей графа начинают с нумерации ветвей дерева, используя но­мера с 1 по у - 1. Номера с «у» по «в» придают ветвям графа, не вошед­шим в выбранное дерево. Их называют ветвями связи, или хордами. В качестве примера на рис. 2.34, а изображена схема, а на рис. 2.34, б — соответствующий ей граф. Схема имеет четыре узла и шесть ветвей. Узлы обозначены цифрами 1-4 (рис. 2.34, 6). На рис. 2.34, в показано дерево, которое положено далее в основу формирования топологических матриц.

Ветви дерева обозначим цифрами /, 2, 3, остальные ветви графа (вет­ви связи) — цифрами 4, 5, 6. Ветви дерева (рис. 2.34, г) вычерчены утол­щенными линиями, ветви связи — тонкими. На ветвях графа ставим стрел­ки, направление их произвольно (см. рис. 2.34, в, г). Узловую матрицу [Л] составляют для всех узлов графа, кроме одного. В этой матрице номер /-й строки соответствует номеру узла, а номер у-го столбца — номеру ветви. В ячейки матрицы [Л] ставят числа 1, - 1, 0. Если узел, для которого составляется строка матрицы, охватить некоторой поверхностью, след которой показан кружком, то в соответствующую ячейку матрицы [Л] ставят I, если стрелка у-ветви направлена из кружка, ставят - I, если стрел­ка направлена в кружок, и 0, если ветвь не затронута кружком.

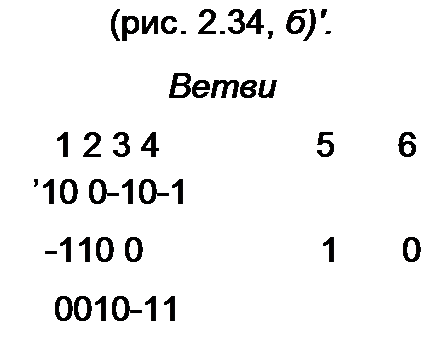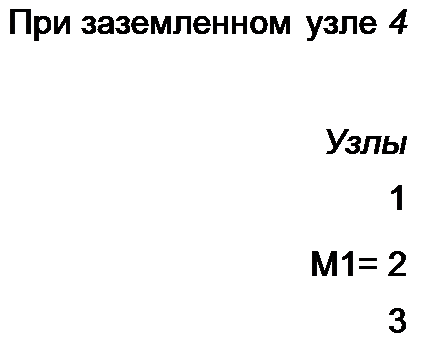Заметим, что матрица [А] может быть представлена двумя подматри­

цами:

Ветви

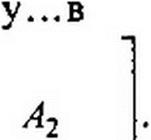Узлы

1

у-1

Матрицу сечений [£>] составляют для любых сечений графа, а матрицу главных сечений ] — для главных сечений выбранного дерева. След се­чений на рисунках показывают овалами, вычерченными тонкими линиями.

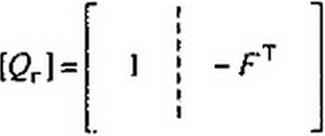
Главными сечениями называют сечения, каждое из которых рассека­ет несколько ветвей связи и только одну ветвь выбранного дерева. Глав­ные сечения нумеруют. Номер главного сечения соответствует номеру рассекаемой этим сечением ветви дерева. Для графа на рис. 2.34, б глав­ные сечения показаны на рис. 2.34, г и обозначены цифрами /, 2, 3. Се­чение / рассекает ветвь 1 и ветви связи 4 и 6, сечение 2 — ветвь 2 и ветви связи 4, 5, 6 (ветвь / целиком входит в овал 2 и не рассекается им), се­чение 3 — ветвь 3 и ветви связи 5 и 6. Строки матрицы [Q_r] соответ­ствуют сечениям, а столбца — ветвям графа.

В ячейках соответствующей строки матрицы [£_г] ставят 1 для рас­секаемой этим сечением ветви дерева и для всех ветвей связи, стрелки на которых ориентированы относительно поверхности этого сечения (след этого сечения на плоскости — овал), так же как и стрелка на рассекаемой этим сечением ветви дерева. Когда стрелка на ветви связи направлена относительно овала иначе, чем стрелка на ветви дерева, ста­вят - 1, когда ветвь связи не рассечена — 0.

Применительно к дереву рис. 2.34, в для главных сечений (см. рис. 2.34, г):

Ветви

Сечения 12345 6

1 Г1 0 0 -1 0 -I

(2_Г]= 2 0 10-11-1

3 [00-10-11

В общем случае матрица [<2J может быть представлена в виде двух матриц:

Ветви

Сечения 1,..(у-1) у...в

I Г !

Каждая строка [0J имеет только по одному элементу 1 и находится он на главной диагонали, поэтому ] представляет собой единичную матрицу [I] и 12_Г] = П 1 Q₂l

Главными контурами называют контуры, в каждый из которых вхо­дит только по одной ветви связи. Нумеруют главные контуры теми же номерами, какие присвоены ветвям связи в них. Главные контуры 4, 5, 6 дерева на рис. 2.34, в изображены на рис. 2.35. Толстыми линиями пока­заны ветви дерева, тонкими — ветви связи.

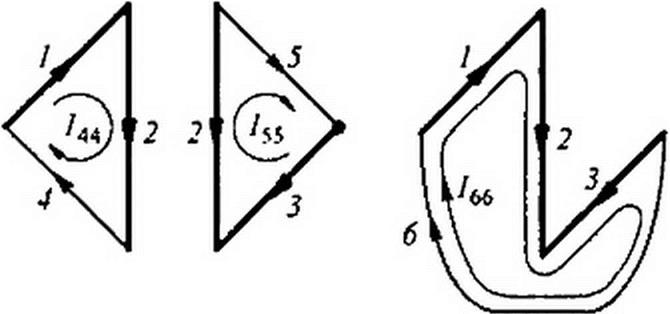
Рис. 2.35

Матрицей главных контуров [К_г] называют матрицу, составленную из чисел 1, - 1,0, строки которой соответствуют номеру главного конту­ра, а столбцы — номеру ветви.

Главные контуры при составлении матрицы [£_г] обходят в направ­лении стрелки на ветви связи соответствующего контура. Если при та­ком обходе контура направление стрелки на какой-либо ветви этого кон­тура совпадает с направлением обхода контура, то в соответствующую ячейку [К,.] ставят 1, если не совпадает, то - 1, если ветвь не обходит­ся, то 0.

Для контуров 4, 5, 6 на рис. 2.35:

Ветви

Контуры J 2 3 4 5 6

4 Г1 1 0 10 0

[К_г] = 5 0-11010

6 11-10 0 1

—

В общем виде матрица [/С_г ] может быть представлена в виде двух подматриц и имеет следующую нумерацию строк и столбцов:

Ветви

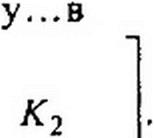Так как номер строки (номер контура) в [АГ₂ ] определяется номером его ветви связи и обход контура осуществляется в соответствии со стрел­кой на ветви связи, то каждая строка подматрицы ] имеет только один элемент 1, расположенный на ее главной диагонали, т. е. представ­ляет собой единичную матрицу []], а [К"_г] = [К] ! 1].

§ 2.32 Запись уравнений по законам Кирхгофа с помощью топо­логических матриц. Совокупность уравнений по первому закону Кирх­гофа может быть записана следующим образом:

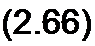И[/_В] = о,

где [/_в]— матрица-столбец (транспонированная матрица-строка) токов ветвей. Для графа на рис. 2.34, г

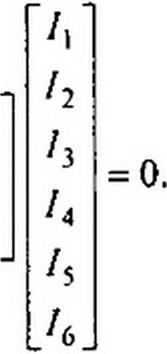Совокупность уравнений по второму закону Кирхгофа может быть Записана так;

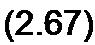(WJ=o,

где [£7_В]—матрица-столбец (транспонированная матрица-строка) напря­жения ветвей. Для графа на рис. 2.34, г

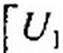О 1 о

1 0 1

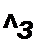
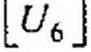
-10 0

§ 2.33 Обобщенная ветвь электрической цепи. В литературе, использующей матрично-топологическое направление теории цепей, вводят понятие обобщенной ветви электрической цепи (рис. 2.36). Она об­разована двумя параллельными ветвями. Первая состоит из сопротивления ветви Я_в (проводимость g₈) и источника ЭД С £_в, вторая — из источни­ка тока J_B. Для принятых на рис. 2.36 положительных направлений токов ток через сопротивление £_в равен /_в + J_B. Напряжение между точками а и b ветви обозначим U_t. Тогда, по закону Ома для участка цепи с ЭДС,

(7_B + £_B=£_B(/_B+J_B) (2.68)

или

(Л+Л) = г_в«4<Л)- (2-69)

§ 2.34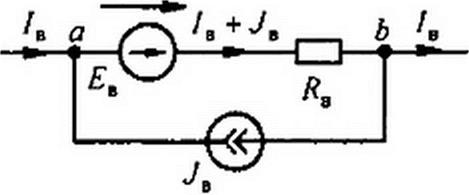

Вывод уравнений метода контурных токов с помощью то­пологических матриц. Уравнение (2.68) справедливо для любой обоб­щенной ветви схемы, а также и для совокупности ветвей, входящих в любой главный контур. Запишем совокупность уравнений (2.68) для всех ветвей, входящих во все главные контуры:

И_гЛУ.1+ИгЛ£в) = Иг][Л_в]{[/.] + [Л]1.

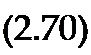
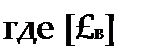— диагональная матрица сопротивлений ветвей.

L «.J

Учтем, что по второму закону Кирхгофа сумма напряжений любого замкнутого контура электрической цепи равна нулю, поэтому [£_г ] [£/_в ] = 0. Кроме того, матрица-столбец токов ветвей [/_в] может быть записана через матрицу-столбец контурных токов [/**] и транспониро­ванную матрицу главных контуров (£_г]^т :

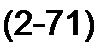1/.]=Иг1^Т (/**]•

При этом полагаем, что контурный ток каждого главного контура на­правлен в соответствии со стрелкой на ветви связи этого контура. Кон­рис. 2.34, г показаны на рис. 2.35.

Отсюда I_} - /₄₄ + /₆₆; /₂ - /₄₄ - /₅₅ + /₆₆; /₃^/₅₅ -/₆₆; /4-/44; /₅-/₅₅; ^6 ⁼ ^66*

Подставив (2.71) в (2.70), получим

Иг][Я»][К_г}^т[/_н] = [К_г][£.]-К_г][Л,][Л]. (2.72)

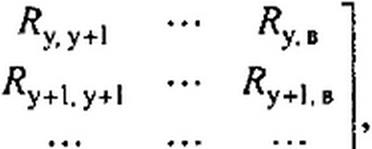
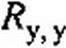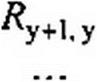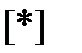Произведение [А7_Г ] [Я_в] [К_г]^т = [*]— матрица контурных сопротивле­ний метода контурных токов. Так как контуры нумеруем от «у» до «в», то

J? р

^/Х В. у ^Ав. y+i

где R_{m т} — полное сопротивление т-контура; R_mn — сопротивление ветви (ветвей), смежной между т- и «-контурами; берется со знаком плюс, если контурные токи 1_{т т} и 1_{п п} текут через смежную ветвь согласно, и со знаком минус, если встречно.

Для рис. 2.34, г, полагая сопротивления ветвей /?₍ -Я₆, имеем

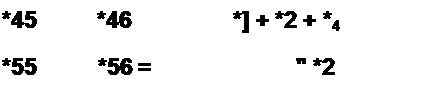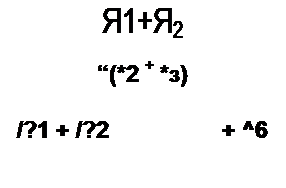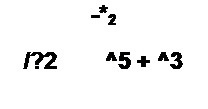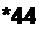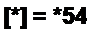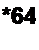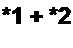Запишем решение (2.72) относительно [/^]:

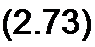[/_и) = {[^И^]И_г]^т}‘¹[К_г]{[£,]-[я_в][Л]}.

§ 2.35 Вывод уравнений метода узловых потенциалов с помощью топологических матриц. Совокупность уравнений (2.69) для у - 1 уз­лов схемы заменим матричным уравнением

M][/_e]+[H][J_e] = M](g_B](t/_B]+M][g_B][E_B].

По первому закону Кирхгофа, [ЛЦ/_В]-О. Матрицу-столбец напряже­ний ветвей [С/_в ] можно записать через транспонированную матрицу (Я] и матрицу-столбец потенциалов незаземленных узлов [<р], т. е. в виде [(/_В] = [Л]^Т [<р]. Для рис. 2.34, г, полагая узел 4 заземленным, имеем

Ф|

<Р2

Фз J

Действительно,

ц^q>i-<р₂; *Л=Фг; ^з=Фз; <Л = -Фь Ц>=фз-фз; Ц>=фз-фг

Таким образом, система уравнений метода узловых потенциалов за­пишется так:

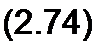И [g, ] И^т [<р] = -[Я] [g, 1 [£, ]+[ A] [J. ],

где [Л] [g_B] [Л]^т =[(7]— матрица узловых проводимостей метода узло­вых потенциалов. При заземленном у-узле

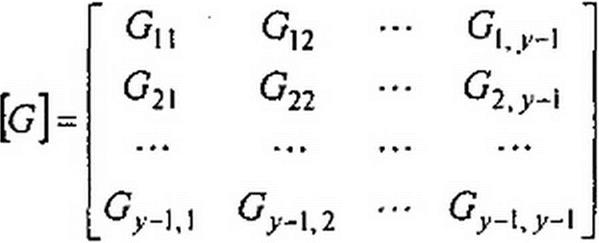Для рис. 2.34, б

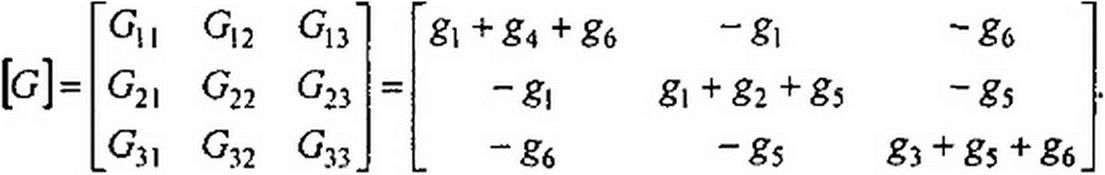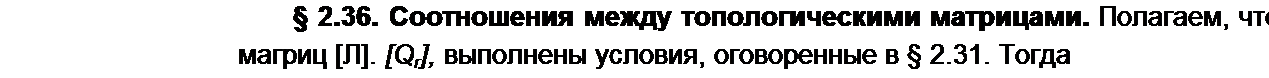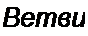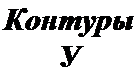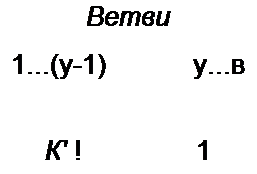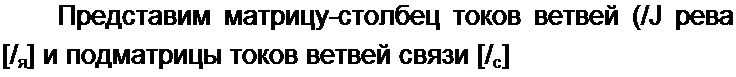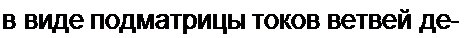Матрицу-столбец напряжений ветвей также представим в виде подматрицы напряжений ветвей дерева [О_д] и подматрицы напряжений ветвей связи {(/<.]:

По первому закону Кирхгофа [Л](/_а] = О или

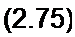И)[/_дк(Л)(/_с]=о.

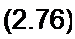Алгебраическая сумма токов в любом сечении схемы равна нулю, поэтому [(?_r](/J = 0. Следовательно,

= (1)(/д] + [С₂](/_с] = 0-

По второму закону Кирхгофа [^_r][t/_e] = 0, поэтому

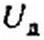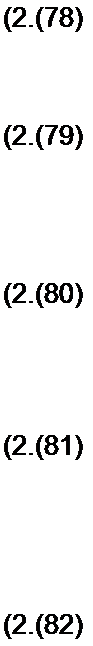
(2.77)

Учтем, что столбец [К,] соответствует строкам если у всех ненулевых элемен­тов изменить знаки. Следовательно,

Обозначим ,

(Г)=(К,]=-1Й]^Т.

Тогда

и_г]= г : । .

Умножив (2.75) слева на [Л]^-1, получим

[/д)=-М|Г’[АИ/с]-

Но из (2.76) имеем [1][/_я] = -\Q₂](41» поэтому

[С₂] = М1Г'(/1₂].

Дадим обоснование еще одному соотношению

ИИ_Г]^Т=О.

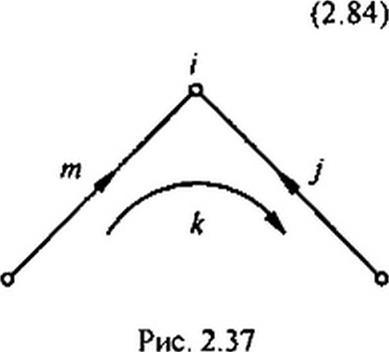
В каждой строке этого матричного произведения складываются произведения элементов /-строки на элементы ^-столбца by. Произведение о_у b_kj не будет нулем, если j вегвь подходит к узлу / и входит в контур к (рис. 2.37). Но в контуре к узел i соединен не с одним, а с двумя узлами ветвями т и j, поэтому всегда будет еще ненулевое произведение a_im Ь^,, отвечающее ветви т, независимо от того, как направлены стрелки на ветвях и каково направление обхода контура к. Следовательно.

каждая строка (2.84) <я,у b_kJ +а_1т Ь_кт = 0.

Соотношения между топологическими матрицами существенны для чета цепей на ЭВМ. Например, записав [(>₂] = -[Т⁷]¹, определяем (F]

§ 2.37. Сопоставление матрично-топологического и традиционно­го направлений теории цепей. В § 2.29 указывалось, что основными ме­тодами расчета электрических цепей являются МУП и МКТ. Оба эти ме­тода могут быть применены в своей традиционной записи: [G] [ср] = [J_kk ] для МУП и [Л] (4* ] = [£**] ^для МКТ либо в матрично-топологической в виде уравнений (2.72) и (2.74). Для задач, встречающихся в курсе ТОЭ, составление систем уравнений традиционным способом (см. § 2.13; 2.22), осуществляемое непосредственно по схеме, значительно проще, быстрее, удобнее и надежнее. Проще и быстрее выполняется и проверка состав­ленных уравнений. Что касается решения составленных уравнений, то системы с относительно небольшим числом уравнений, записанные в тра­диционной форме, могут быть решены с помощью микрокалькулятора. Системы с большим числом уравнений в том и другом случае решают с помощью ЭВМ.

Положительная сторона матрично-топологического направления тео­рии цепей заключается в большой степени упорядоченности составления систем уравнений. Если ввести определенную иерархию ветвей электри­ческих цепей по наличию и отсутствию в них источников питания, ин­дуктивных и емкостных элементов, индуктивных сечений и емкостных контуров, то могут быть составлены алгоритмы, позволяющие осуществ­лять с их помощью так называемое машинное проектирование. Под машинным проектированием понимают числовые расчеты на ЭВМ относительно сложных систем на оптимальный в том или ином смысле режим их работы. Совокупность вопросов, относящихся к машинному проектированию, в настоящее время усиленно разрабатывается, однако многие из них выходят за рамки курса ТОЭ и составляют предмет специальных курсов, В заключение можно сказать, что традиционное и матрично-топологическое направления теории цепей дополняют друг друга и потому студент должен владеть обоими направлениями. При выполнении повседневных инженерных расчетов и решении задач, встре­

чающихся в курсе ТОЭ, целесообразнее пользоваться уравнениями тео­рии цепей в их традиционной форме записи, при машинном проектиро­вании — в матрично-топологической форме.

Вопросы для самопроверки

§ 1.1 еделите понятия «электрическая цепь», «электрическая схема», «узел», «устра­нимый узел», «ветвь», «источник ЭДС» и «источник тока». 2. Как выбирают положитель­ные направления для токов ветвей и как связаны с ними положительные направления напряжений на сопротивлениях? 3. Что понимают под ВАХ? 4. Нарисуйте ВАХ реального источника, источника ЭДС, источника тока, линейного резистора. 5. Сформулируйте за­кон Ома для участка цепи с ЭДС, первый и второй законы Кирхгофа. Для двух законов Кирхгофа дайте по две формулировки. 6. Чем следует руководствоваться при выборе кон­туров, для которых следует составлять уравнения по второму закону Кирхгофа? Почему ни в один из этих контуров не должен входить источник тока? 7. Поясните этапы постро­ения потенциальной диаграммы. 8. В чем отличие напряжения от падения напряжения? 9, Охарактеризуйте основные этапы метода контурных токов (МКТ) и метода узловых потенциалов (МУП). При каком условии число уравнений по МУП меньше числа уравне­ний по МКТ? 10, Сформулируйте принцип и метод наложения. 11. Сформулируйте и до­кажите теорему компенсации. 12. Запишите и поясните линейные соотношения в элект­рических цепях. 13. Что понимают под входными и взаимными проводимостями? Как их определяют аналитически и как опытным путем? 14. Покажите, что метод двух узлов есть частный случай МУП. 15. Приведите примеры, показывающие полезность преобразова­ния звезды в треугольник и треугольника в звезду. 16. Сформулируйте теорему компенса­ции и теорему вариаций. 17. Дайте определение активного двухполюсника, начертите две его схемы замещения, найдите их параметры, перечислите этапы расчета методом экви­валентного генератора. 18. Запишите условие передачи максимальной мощности нагруз­ке. Каков при этом КПД? 19. Покажите, что если в линейной цепи изменяются сопро­тивления в каких-то двух ветзях, то три любых тока (напряжения) связаны линейной зависимостью вида ~ = а + b х + су. 20. Выведите формулы преобразования треугольни­ка в звезду, если 8 ветвях треугольника кроме резисторов имеются и источники ЭДС. 21. В электрической цепи известны токи в двух ветвях — к и т (1_к и !„). Сопротивле­ния в этих ветвях получили приращения ДЯ* и Полагая известными входные и взаимные проводимости ветвей к, т, г, определите приращения токов в ветвях к, т, г, т. е. Д/*, Д/_Л, д/_г. 22. Какие топологические матрицы вы знаете? 23. Запишите урав­нения по законам Кирхгофа с использованием матриц [Л] и [Х_г]. 24. Что понимают под обобщенной ветвью? 25. Выразите токи ветвей через контурные токи и матрицу [£_г]. 26. Выразите напряжения ветвей через потенциалы узлов и матрицу [Л]. 27. Выведите урав­нения метода узловых потенциалов, используя матрицы [Л]. [g_B] и [Л]^т. 28. Выведите уравнения метода контурных токов, используя матрицы [KJ, |/?_е] и (А?_г]^т. 29. Охарак­теризуйте сильные и слабые стороны матрично-топологического направления теории це­пей. 30. Решите задачи 1.2. 1.7, 1.10, 1.13. 1.10, 1.24, 1.33, 1.40, 1.41, 1.45 из сборника задач [39].

Глава третья

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА

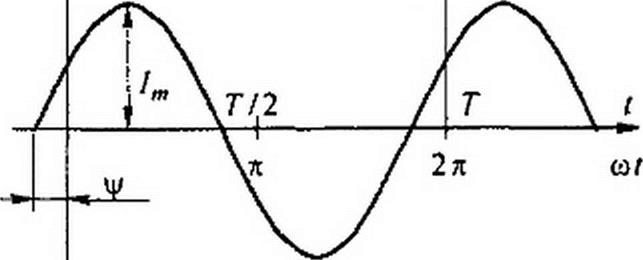
§ 1.2 Синусоидальный ток и основные характеризующие его ве­личины. Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (рис. 3.1):

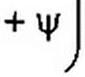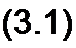Максимальное значение функции называют амплитудой. Амплитуду тока обозначают 1_т. Период Т — это время, за которое совершается одно полное колебание.

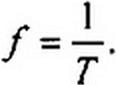Частота f равна числу колебаний в 1 с (единица частоты/— герц (Гц) или с^-1):

(3.2)

Угловая частота о (единица угловой частоты — рад / с или с ¹)

со = 2 л / = 2 л/Г. (3.3)

Аргумент синуса, т. е. (<о t + у), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.

Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой.

В странах СНГ и Западной Европы наибольшее распространение по­лучили установки синусоидального тока частотой 50 Гц, принятой в энер­гетике за стандартную. В США стандартной является частота 60 Гц. Диапазон частот практически применяемых синусоидальных токов очень широк: от долей герца, например в геологоразведке, до миллиардов герц в радиотехнике.

Синусоидальные токи и ЭДС сравнительно низких частот (до несколь­ких килогерц) получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью различных полупроводниковых генераторов (подробно рассматриваемых в курсе радиотехники и менее подробно — в курсе ТОЭ). Источник синусоидальной ЭДС и источник синусоидаль­ного тока обозначают на электрических схемах так же, как и источники постоянной ЭДС и тока, но обозначают их е иу (или е(Г) иу(/)).