Принцип наложения положен в основу метода расчета, получившего название метода наложения.

Дата: 2025-06-02; Просмотры: 12

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

При расчете цепей данным методом поступают следующим образом: поочередно рассчитывают токи, возникающие от действия каждой из ЭДС, мысленно удаляя остальные из схемы, но оставляя в схеме внут­ренние сопротивления источников, и затем находят токи в ветвях путем алгебраического сложения частичных токов. Заметим, что методом на­ложения нельзя пользоваться для подсчета выделяемых в сопротивлени­ях мощностей как суммы мощностей от частичных токов, поскольку мощность является квадратичной функцией тока (Р = R /²).

Если через некоторое сопротивление R протекают согласно направ­ленные частичные токи и /₂, то выделяемая в нем мощность P = /?(Zj + /₂)² и не равна сумме мощностей от частичных токов: Р * R Е + R I}.

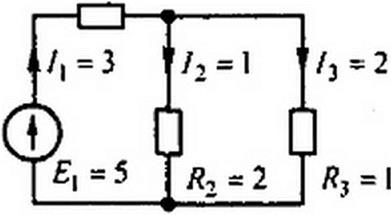
Пример 14. Для схемы (рис. 2.14, а) методом наложения найти токи в ветвях, опре­делить мощности, отдаваемые в схему источником тока и источником ЭДС, полагая /?1 = 2 Ом; /?₂ = 4 Ом; R) ~ 6 Ом; J = 5 А; Е = 20 В.

Решение. Положительные направления токов в ветвях принимаем в соответствии с рис. 2.14, а. С помощью схемы на рис. 2.14, 6 (источник ЭДС удален, зажимы cd закоро­чены) найдем токи в ветвях от действия источника тока:

/: = А5А; /; = /{ =5— -ЗА; /1=2 А.

^{1 2 1}Л₂ + /?_} 4 + 6 ³

Используя рис. 2.14, в, подсчитываем токи в ветвях от действия источника ЭДС (за­жимы ab разомкнуты, так как внутреннее сопротивление источника тока равно бесконеч­ности):

Результирюшие токи в ветвях вычислим, алгебраически суммируя соответствующие частичные токи этих двух режимов:

/₁ = /₁' + /₁'=5 + О = 5А; /₂ = /'-/? = 3-2 = 1А; /₃ = /^ + /₃' = 2 + 2 = 4А;

Ф_о = Фл + Мг +'Л; С/_яА = 1-4 + 5-2 = 14В.

Мощность, отдаваемая в схему источником тока, U_a/l J -14 ■ 5 = 70 Вт. Мощность, от­даваемая в схему источником ЭДС, Е /₃ = 20 ■ 4 = 80 Вт.

Уравнение баланса мощности /₍² /?, + /j + /₃ R_y-U_ahJ + Е /₃

§ 2.15. Входные и взаимные проводимости ветвей. Входное сопро­тивление. На рис. 2.15, а изображена так называемая скелетная схема пассивной цепи. На ней показаны ветви и узлы. В каждой ветви имеется сопротивление. Выделим в схеме две ветви: тик. Поместим в ветвь т ЭДС Е_т (других ЭДС в схеме нет). Выберем контуры в схеме так, что­бы А-ветвь входила только в А-контур, а /л-ветвь — только в /п-контур. ЭДС Е„, вызовет токи в ветвях кит;

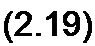Л 8кт>

т ~ 8шт’

Коэффициенты g имеют размерность проводимости/

Коэффициент g с одинаковыми индексами (g„_w) называют входной проводимостью ветви (ветви т). Он численно равен току в ветви т, воз­никшему от действия ЭДС Е_т = I В (единичной ЭДС): 1„, =1 g_mm.

Коэффициенты g с разными индексами называют взаимными прово­димостями. Так, g_knl есть взаимная проводимость к- и /и-ветвей. Вза­имная проводимость g_km численно равна току в /r-ветви, возникающему от действия единичной ЭДС в w-ветви*’.

Входные и взаимные проводимости ветвей используют при выводе общих свойств линейных электрических цепей (см. § 2.16 и 2.18) и при расчете цепей по методу наложения (см.формулу (2.18)).

Входные и взаимные проводимости могут быть определены расчет­ным и опытным путями.

При их расчетном определении составляют уравнения по методу контурных токов, следя за тем, чтобы ветви, взаимные и входные прово­димости которых представляют интерес, входили каждая только в свой контур. Далее находят определитель системы д и по нему необходимые алгебраические дополнения:

8 кт ~ &кт (2.21)

По формуле (2.21) g_k„, может получиться либо положительной, либо отрицательной величиной. Отрицательный знак означает, что ЭДС Е_т, направленная согласно с контурным током в w-ветви, вызывает ток в Л-ветви, не совпадающей по направлению с произвольно выбранным на­правлением контурного тока 1_к по А-ветви.

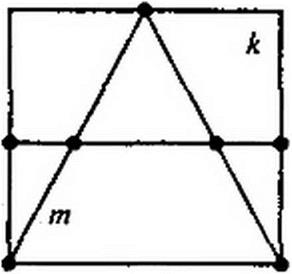
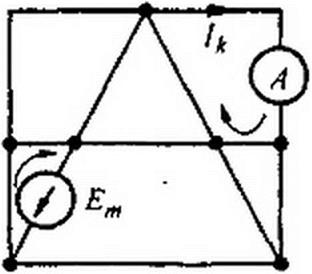
При опытном определении g_mm и g_km в ги-ветвь схемы (рис. 2.15, б) включают источник ЭДС Е,_и, а в А-ветвь — амперметр (миллиампер­метр). Поделим ток 1_к на ЭДС Е_т и найдем значение g_km. Для опреде­ления входной проводимости g_mm ветви т необходимо измерить ток в этой ветви, вызванной ЭДС Е_т. Частное от деления тока т-ветви на ЭДС m-ветви и дает g_mm.

*' Входные и взаимные проводимости ветвей можно определить и иначе: входная проводимость т-ветви — это коэффициент пропорциональности между током и ЭДС этой ветви (при отсутствии ЭДС в других ветвях схемы); взаимная проводимость ветвей к и т — коэффициент пропорциональности между током ^-ветви и ЭДС /n-ветви при отсут­ствии ЭДС в других ветвях схемы.

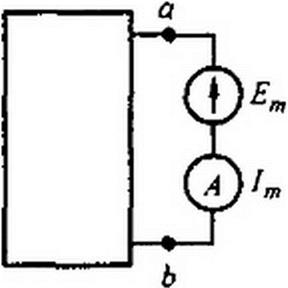
Выделим /и-ветвь, обозначив всю остальную часть схемы (не содержащую ЭДС) некоторым пря­моугольником (рис. 2.16). Вся схема, обозначенная прямоугольником, по отношению к зажимам ab об­ладает некоторым сопротивлением. Его называют входным сопротивлением. Входное сопротивление /77- ветви обозначим Тогда

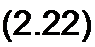, -5*- ¹ - ^Д ВХ т г д

‘ т Sтт & тт

Таким образом, входное сопротивление m-ветви есть величина, обрат­ная входной проводимости этой ветви. Его не следует смешивать с пол­ным сопротивлением /и-контура в методе контурных токов.

Пример 15. Определить входную g_u и взаимную g₁₂ проводимость в схеме рис. 2.13.

Решение. Контуры выбраны так. что ветвь I (ветвь cbm) с источником ЭДС вхо­дит только в первый контур, а ветвь 2 (ветвь са) с источником ЭДС Е₂ — во второй.

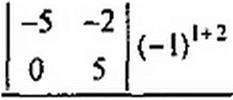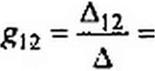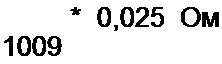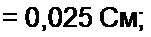Поэтому можно воспользоваться определителем системы Д и алгебраическими допол­нениями Д_п и Д₁₂, составленными но данным примера 13:

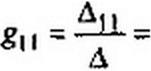
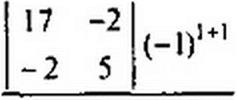
О )

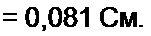——*0,081 Ом"¹

1009

§ 2.16. Теорема взаимности. Теорема взаимности формулируется следующим образом: для любой линейной цепи ток в k-ветви, вызван­ный источником ЭДС Е_т, находящимся в т-ветви, I_k = Е_П1 g_km равен току в т-ветви, вызванному источником ЭДС Е_к (численно равной ЭДС Е,„), находящимся в А-ветви, /„, - E_k g_lllk.

Для доказательства теоремы взаимности обратимся к рис. 2.15, а. Как и при выводах в § 2.15, выделим две ветви схемы: к- и m-ветви. Включим в ветвь т источник ЭДС Е_Л), в ветвь к — амперметр А. Амперметр для измерения тока /_к включаем только для наглядности; сопротивление ам­перметра полагаем равным нулю. Пусть каждая из ветвей к и т входит соответственно только в к- и т-контуры. Поэтому по методу контурных токов I_k - Е_т Поменяем местами источник ЭДС и амперметр,

т. е. источник ЭДС переместим из т- в Л-ветвь и назовем теперь Е_к, а амперметр — из к- в m-ветвь. В этом случае ток 1„, = Е_к Л_тк / △.

Так как Е_к = Е_т, а \_тк = Ь_кт в силу симметрии определителя систе­мы Д относительно главной диагонали (см. § 2.13), то ток 1_к в схеме на рис 2.15, б равняется току /_л) в схеме на рис. 2.15, в.

При практическом использовании теоремы взаимности важно иметь в виду взаимное соответствие направлений токов и ЭДС в схемах на рис. 2.15, б, в.

Так, если ЭДС Е_к источника ЭДС, находящегося в £-ветви схемы (рис. 2.15, в), направлена согласно с контурным током 1_к (рис. 2.15, б), то положительное направление отсчета для тока 1_т (рис. 2.15, в) будет совпадать с положительным направлением контурного тока по ветви т (ЭДС Е_т в схеме на рис. 2.15, б направлена по /_т).

Для нелинейных цепей теорема (принцип) взаимности невыполнима. Цепи, для которых не выполняется принцип взаимности, называют необратимыми.

Пример 16. В схеме на рис. 2.17 переключатели Д, Р₂, Ру, и Р₄ могут находиться в первом или во втором положении. Если они находятся в положении 1, то включен толь­ко один источник ЭДС Е₄. Под действием ЭДС £₄ протекают токи /| = 1,5А, /₂=ЗА,

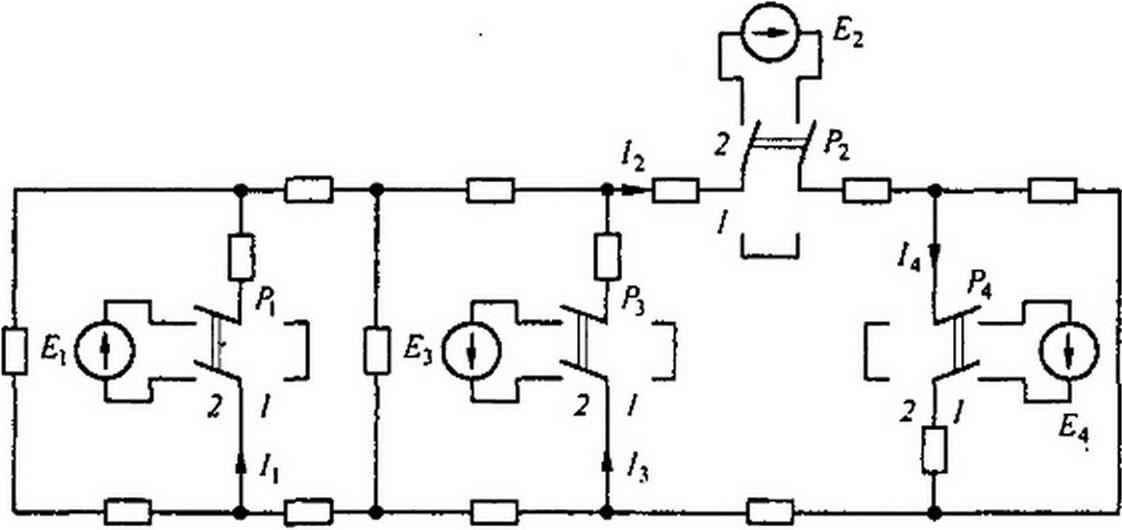
Рис. 2.17

!у ~ I А. Найти ток /₄, если все переключатели находятся в положении 2. полагая, что £, ° 20 В, £₂ =40 В. £,=50В. £₄ = 10В.

Решение. Для определения тока /₄ воспользуемся принципом наложения и прин­ципом взаимности. Если бы в схеме был включен один источник ЭДС £j = 10 В. а осталь­ные (£₂ и £₃) отсутствовали, то в ветви 4’¹ по принципу взаимности протекал бы сверху вниз ток в 1.5 А. Так как ЭДС £,=20 8. то в ветви 4 протекает ток, равный 1,5-20/10 = 3 А. Аналогичным образом найдем токи в ветви 4 при включении источников ЭДС £₂ и Е₃ и произведем алгебраическое сложение частичных токов (с учетом их направления):

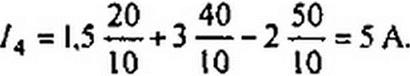
§ 2.17 Теорема компенсации. Рассмотрим два варианта этой теоре­мы. В любой электрической цепи без изменения токораспределения сопротивление можно заменить:

1) источником ЭДС, ЭДС которого численно равна падению напряже­ния на заменяемом сопротивлении и направлена встречно току в этом сопротивлении;

2) источником тока J, ток которого численно равен току в этом сопро­тивлении и имеет то же направление, что и ток /.

’* Номер ветви соответствует индексу ЭДС.

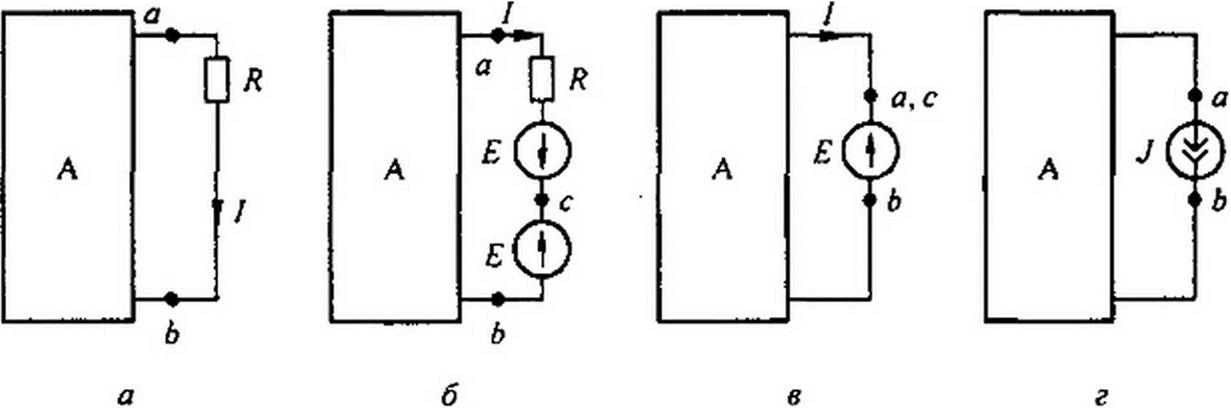
Для доказательства теоремы компенсации выделим из схемы одну ветвь с сопротивлением R, по которой течет ток /, а всю остальную часть схемы условно обозначим прямоугольником (рис. 2.18, а).

Если в выделенную ветвь включить два одинаковых и противоположно направленных источника ЭДС Е, ЭДС которых равна падению напряже­ния на сопротивлении R под действием тока / (Е ~ / /?; рис. 2.18, 6), то ток / в цепи от этого не изменится. Убедимся, что разность потенциа­лов между точками а и с на рис. 2.18, б при этом равна нулю. Действи­тельно,

ф_с =Ф_а-/Е+Е = ф_д- / R + l R-y_a.

Если ф_с =ф_а, то точки а и с можно объединить в одну, т. е. закоро­тить участок ас и получить схему, где вместо сопротивления R включен источник ЭДС Е (см. рис. 2.18, в).

Схема, соответствующая второму варианту теоремы, изображена на рис. 2.18, г. Чтобы прийти к ней, заменим последовательно соединенные R и Е на участке ас (см. рис. 2.18, б) параллельным соединением источ­ника тока J = Е/Е = / и сопротивления R. Так как U_at. - 0, то ток через R будет отсутствовать и потому R можно удалить из схемы.

Если ЭДС Е участка Ьс включить в состав источника тока, то полу­чим схему, где напряжение U_ba = -/ R (рис. 2.18, г).

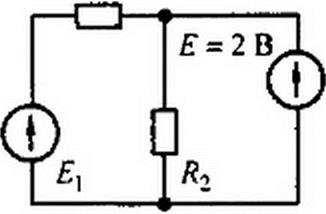
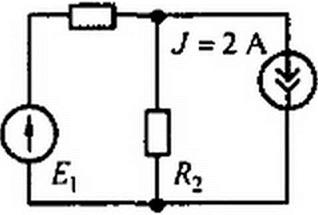
Пример 17. На схеме (рис. 2.19, а) даны значения R (Ом), ЭДС (В) и токов / (А). Заменить Ry источником ЭДС и источником тока.

Решение. На рис. 2.19. б изображена схема с источником ЭДС Е = 2В. а на рис. 2.19, в — с источником тока J - 2 А.

§ 2.18. Линейные соотношения в электрических цепях. Если в ли­нейной электрической цепи изменяется ЭДС или сопротивление в какой- либо одной ветви, то две любые величины (токи и напряжения) двух любых ветвей связаны друг с другом линейными зависимостями вида

у = а + b х.

Функцию х выполняет ток или напряжение одной ветви, функцию у — ток или напряжение другой ветви.

Доказательство. Согласно методу контурных токов, общее вы­ражение для тока в А-ветви записывают в виде (2.18). Если в схеме изме­няется только одна ЭДС, например ЭДС Е_т, то все слагаемые в (2.18), кроме слагаемого Е_т g_km, постоянны и могут быть для сокращения записи заменены некоторым слагаемым А_к.

Следовательно,

(2-23)

Аналогично, для /?-ветви

(2-24)

Найдем Е_п, из (2.24):

__ р

nt

Spm

и подставим в (2.23). Получим

(2.25)

ГДе &к ~ Л_к Ар Skni’ &к Skm^Spnr

Коэффициенты а_к и Ь_к могут быть $0. В частном случае либо а_к, либо Ь_к может быть равно нулю.

Равенство (2.25) свидетельствует о том, что при изменении ЭДС Е_т Локи 1_к и /р связаны линейной зависимостью. Из теоремы компенса­ции известно, что любое сопротивление можно заменить источником ЭДС. Следовательно, изменение сопротивления в /и-ветви эквивалентно изменению ЭДС Е_т. Таким образом, линейное соотношение между дву­мя любыми токами (2.25) имеет место при изменении не только ЭДС Е_п1, но и сопротивления некоторой w-ветви.

Если обе части (2.23) умножить на сопротивление А-ветви R_k и про­делать аналогичные выкладки, то можно убедиться в том, что напряже­ние Л-ветви линейно связано с током в р-ветви.

Коэффициенты а_к и Ь_к из (2.25) и в других подобных выражениях могут быть найдены расчетным или опытным путем.

При опытном определении коэффициентов достаточно найти значе­ния двух токов (соответственно напряжений) при двух различных режи­мах работы схемы и затем решить систему из двух уравнений с двумя
неизвестными. Пусть, например, в первом опыте I_k = l_ki и l_p-i_p\, а во втором 1_к=1_к2 и ^_Р-^_Р2-

Тогда

^2 ~^ак ⁺^к 1_Р2>

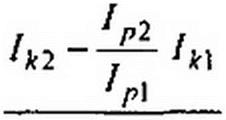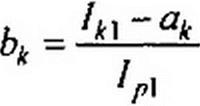Если в схеме одновременно изменяются ЭДС или сопротивления в каких-либо двух ветвях, то любые три величины в этой схеме (токи, на­пряжения) связаны друг с другом линейным соотношением вида у ~ a + b х + с z.

Доказательство этого соотношения проводится аналогично приведен­ному ранее.

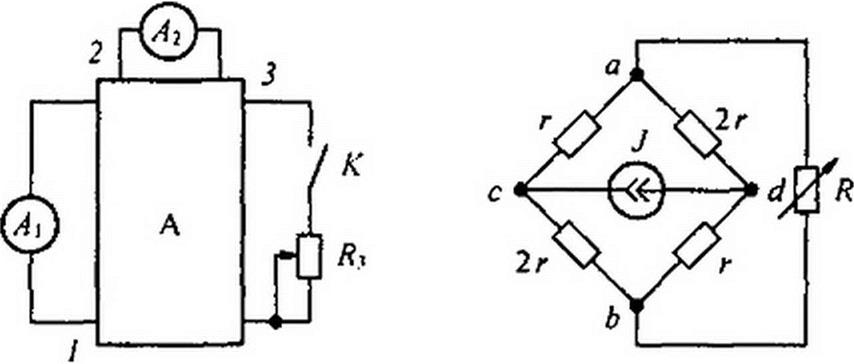
Пример 18. На рис. 2.20, а изображена схема, в которой выделены три ветви, В вет­ви / включен амперметр Л], в ветви 2 — амперметр Л₂. В ветви 3 имеются ключ К и сопротивление Если К разомкнут, то амперметр показывает 1 А, амперметр А₂ — 5 А. При замкнутом ключе амперметр л. показывает 2 А, а амперметр Л₂ — 4 А. При замкнутом ключе сопротивление fy изменили так, что показание амперметра Л₂ стало 4,5 А. Каково показание амперметра А_} в этом режиме?

Решсние. Выразим /, через /₂ : 1\=а + Ь1₂. Составим уравнение для определе­ния а и Ь.

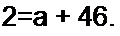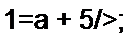Отсюда а ~ 6 и b ~ -1. При Д =4,5 А; /₍ =6-4,5 = 1.5 А.

Пример 19. В схеме (рис. 2.20, б) сопротивление R изменяется от нуля до бесконеч­ности. Вывести зависимость напряжения U_cj от напряжения U_oh.

3 г J

Решение. При разомкнутой ветви ab (J_cct ~ — rJ и Ц_(Л = —. При коротком замы-

3 4 ।

кании ветви ab LJ_cj~ — rJ и (/_аА=0. Отсюда a = — rj и Ь-—. Следовательно, 4 3 3

J J

а б

Рис. 2.20

§ 2,19. Изменения токов ветвей, вызванные приращением сопро­тивления одной ветви (теорема вариаций). На рис. 2.21, а выделим ветви / и 2 с токами 1_} и /₂, заключив остальную часть схемы вместе с

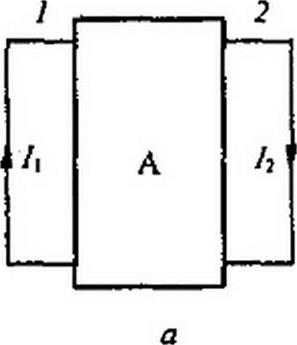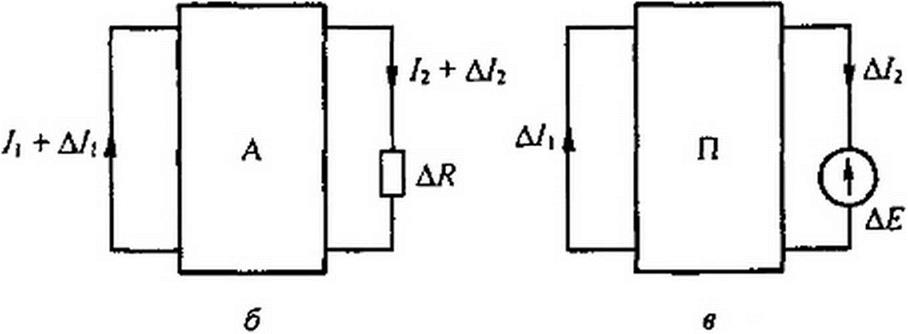
источниками энергии в прямоугольник А (активный); проводимости g|₂ и g₂₂ полагаем известными. Пусть сопротивление ветви 2 изменилось на bR (рис. 2.21, б), в результате чего токи стали

/| +AZ] и /₂ + Д/₂

В соответствии с теоремой компенсации заменим ДЕ на ЭДС

ДЕ = ДЕ (/₂ + Д/₂),

направленную встречно току /₂. На основании принципа наложения можно сказать, что приращения токов A/_t и Д/₂ вызваны ЭДС ДЕ в схеме (рис. 2.21, в), в которой часть схемы, заключенная в прямоуголь­ник, стала пассивной (буква П). Так как схема внутренних соединений и значения сопротивлений в схеме прямоугольника остались без измене­ний, то проводимости g₎₂ и g₂₂ в схеме на рис. 2.21, в имеют те же зна­чения, что и на рис. 2.21, а. Для схемы на рис. 2.21, в имеем:

А/] = -ДЕ g|₂ - “g)2 (Л ⁺^з)’

Д/₂ = -ДЕ g₂₂ = -g₂₂ ДЕ (/₂ +АЛ)>

Знаки минус поставлены потому, что ЭДС АЕ₂ направлена встречно току /₂. Отсюда

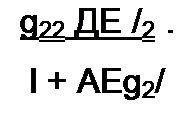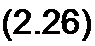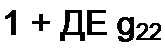Соотношения (2.26) позволяют определить изменение токов в ветвях Z и 2, вызванные изменением сопротивления в ветви 2.

Пример 20. В схеме (рис. 2.21) #₂₂ = 5 / 26См, £₁₂ = 3/26См. Токи /_t=7A, /₂ = 3 А. Определить токи /₍ и /₂ после того, как сопротивление ветви 2 возросло на ДЯ = 1Ом.

Р е ш е н и е. По формулам (2.26), д/, « -0,29 А, Д1₂ ~ “0.483 А: /[ = /_t + Д/, = 6.71 А, Г_г = /₂ + А^ = 2,517 А.

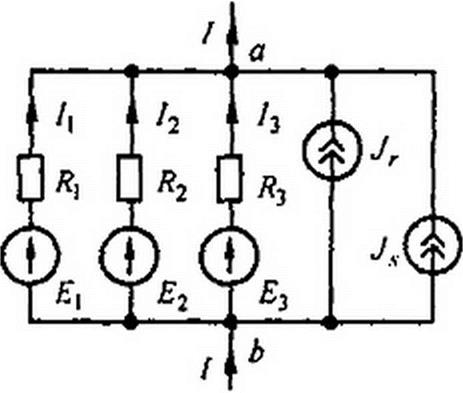
§ 2.20. Замена нескольких параллельных ветвей, содержащих ис­точники ЭДС и источники тока, одной эквивалентной. Расчет слож­ных схем упрощается при замене нескольких параллельно включенных ветвей, содержащих источники ЭДС, источники тока и сопротивления, одной эквивалентной ветвью.

Участок цепи на рис. 2.22, б эквивалентен участку цепи на рис. 2.22, а, если при любых значениях тока /, подтекающего из всей остальной, не показанной на рисунке части схемы, напряжение на зажимах а и b (U_ab)

в обеих схемах одинаково. Для того чтобы выяснить, чему равняются и Е_уу составим уравнения для обеих схем.

Для схемы на рис. 2.22, а

1_}+I2+1₃+J_r+J_x*]y

A=“^^L=(£₁-^)g₁;

/₂ «= {£>2 ~U_ah)

(2.27)

I_n-(Е„ -U_ah) g„

Следовательно,

п <1 п

^Ъ^Ек g4 + t^*“^Zg*>
4=1 4=1 4=1

где п — число параллельных ветвей с источниками ЭДС; q — число па­раллельных ветвей с источниками тока.

Для схемы на рис. 2.22, б

(2.29) где

Равенство токов / в схемах (см. рис. 2.22, а, б) должно иметь место при любых значениях U_ab, а это возможно только в том случае, когда коэффициент при U_ah (2.29) равен коэффициенту при U_ah в (2.28).

Следовательно,

п

(2.30)

*=1

Если слагаемые с U_ab в (2.28) и (2.29) равны и токи / по условию эквивалентности двух схем также равны, то

Х^Ек ёк + ХЛ = ^Ез g>,

*=) Л=1

откуда

и </

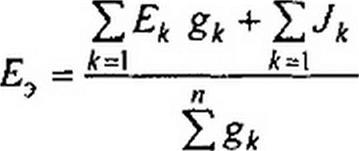
Формула (2.30) дает возможность найти проводимость g₃ и по ней R.₃ в схеме на рис. 2.22, б. Из этой формулы видно, что проводимость g₃ не зависит от того, есть в ветвях схемы (рис. 2.22, а) ЭДС или нет.

При подсчетах по формуле (2.31) следует иметь в виду следующее:

1 ) если в какой-либо ветви схемы ЭДС отсутствует, то соответствую­щее слагаемое в числителе (2.31) выпадает, но проводимость этой ветви в знаменателе (2.31) остается;

2 ) если какая-либо ЭДС в исходной схеме имеет направление, обрат­ное изображенному на рис. 2.22, а, то соответствующее слагаемое вой­дет в числитель формулы (2.31) со знаком минус.

Ветви схемы (рис. 2.22, а, б) эквивалентны только в смысле поведе­ния их по отношению ко всей остальной части схемы, не показанной на рисунке, но они не эквивалентны в отношении мощности, выделяющей­ся в них.

Качественно поясним это. В ветвях схемы на рис. 2.22, а токи могут протекать даже при / = 0, тогда как в ветви ab на рис. 2.22, б при / = 0 ток и потребление энергии отсутствуют.

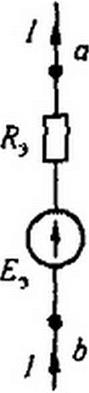
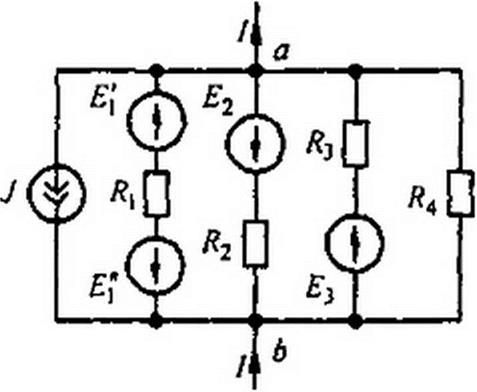
Пример 21. Заменить параллельные ветви (см. рис. 2,22. в) одной эквивалентной. Дано: £]'=10В; £f=30B; £₂=40В; £₃=60В; Я, = 2 Ом; Я₂ = 4 0м; £₃ = 1Ом; /?₄ = 5 0м; J ”■ 6 А.

Решение. Находим:

£[=0,5См; #₂ =0,25 См; £_э = 1См; £₄=0,2См;

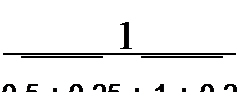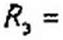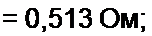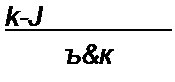
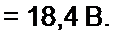(10-30) 0.5-40 0,25 + 60 1-6
1,95

Таким образом, для эквивалентной ветви (рис. 2.22, б) = 0,513 Ом; £_э = 18,4 В.

3 2.21. Метод двух узлов. Часто встречаются схемы, содержащие все­го два узла (рис. 2.23). Наиболее рациональным в них является метод двух узлов.