Свойства линейных электрических цепей и методы их расчета. Электрические цепи постоянного тока

Дата: 2025-06-02; Просмотры: 18

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

§ 2.1 Определение линейных и нелинейных электрических цепей. Электромагнитное устройство с происходящими в нем и в окружающем его пространстве физическими процессами в теории электрических цепей заменяют некоторым расчетным эквивалентом — электрической цепью.

Электрической цепью называют совокупность соединенных друг с другом источников электрической энергии и нагрузок, по которым может протекать электрический ток. Электромагнитные процессы в электрической цепи можно описать с помощью понятий «ток», «напря­жение», «ЭДС», «сопротивление» («проводимость»), «индуктивность», «емкость».

Постоянным током называют ток, неизменный во времени. По­стоянный ток представляет собой направленное упорядоченное движе­ние частиц, несущих электрические заряды.

Как известно из курса физики, носителями зарядов в металлах яв­ляются свободные электроны, а в жидкостях — ионы. Упорядоченное движение носителей зарядов в проводниках вызывается электрическим полем, созданным в них источниками электрической энергии. Источни­ки электрической энергии преобразуют химическую, механическую и другие виды энергии в электрическую. Источник электрической энергии характеризуется величиной и направлением ЭДС, а также величиной внут­реннего сопротивления.

Постоянный ток принято обозначать буквой /, ЭДС источника — Е, сопротивление — /?, проводимость — g. В Международной системе еди­ниц (СИ) единица тока — ампер (А), единица ЭДС — вольт (В), едини­ца сопротивления — ом (Ом), единица проводимости — сименс (См).

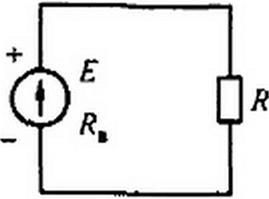
Изображение электрической цепи с помощью условных знаков назы­вают электрической схемой (рис. 2.1, а).

Зависимость тока, протекающего по сопротивлению, от напряжения на этом сопротивлении называют вольт-амперной характеристикой (ВАХ).

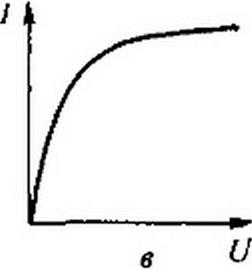По оси абсцисс на графике обычно откладывают напряжение, а по оси ординат — ток.

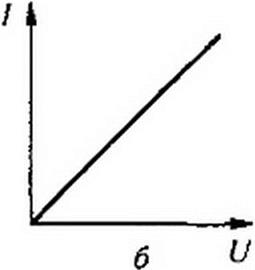
Сопротивления, ВАХ которых являются прямыми линиями (рис. 2.1, б), называют линейными, электрические цепи только с линей­ными сопротивлениями —линейными электрическими цепями.

Сопротивления, ВАХ которых не являются прямыми линиями (рис. 2.1, в), т. е. они нелинейны, называют нелинейными, а электриче­ские цепи с нелинейными сопротивлениями — нелинейными электриче­скими цепями.

§ 2.2 Источник ЭДС и источник тока. Источник электрической энергии характеризуется ЭДС Е и внутренним сопротивлением /?₈. Если через него под действием ЭДС Е протекает ток /, то напряжение на его зажимах U = Е-1 /?_в при увеличении I уменьшается. Зависимость на­пряжения U на зажимах реального источника от тока / изображена на рис. 2.2, а.

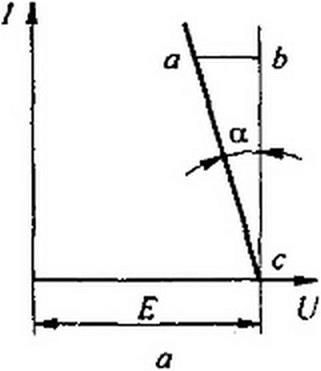
Рис. 2.2

Обозначим через m_lt — масштаб по оси U, через т/ — масштаб по оси /. Тогда для произвольной точки на характеристике рис. 2.2, а ab т_и = / Я_в; be ГП] = /; tga = ablbc - R* т, /т₍₁. Следовательно, tga пропорционален R₃. Рассмотрим два крайних случая.

> 1. Если у некоторого источника внутреннее сопротивление R* = 0, то ВАХ его будет прямой линией (рис. 2.2, б). Такой характеристикой обла­дает идеализированный источник питания, называемый источником ЭДС. Следовательно, источник ЭДС представляет собой такой идеализирован­ный источник питания, напряжение на зажимах которого постоянно (не зависит от тока Г) и равно ЭДС Е, а внутреннее сопротивление равно нулю.

2. Если у некоторого источника беспредельно увеличивать ЭДС Е и внутреннее сопротивление то точка с (рис. 2.2, а) отодвигается по оси абсцисс в бесконечность, а угол а стремится к 90° (рис. 2.2, в). Такой источник питания называют источником тока.

Следовательно, источник тока представляет собой идеализированный источник питания, который создает ток J = /, не зависящий от сопротив­ления нагрузки, к которой он присоединен, а его ЭДС £_ит и внутреннее сопротивление /?_ит равны бесконечности. Отношение двух бесконечно больших величин Е_т / R_m равно конечной величине — току J источ­ника тока.

При расчете и анализе электрических цепей реальный источник электрической энергии с конечным значением /?_в заменяют расчетным эквивалентом. В качестве эквивалента может быть взят:

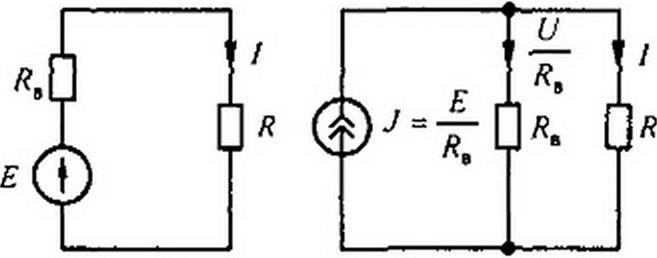
а) источник ЭДС Е с последовательно включенным сопротивлением R_B, равным внутреннему сопротивлению реального источника (рис. 2.3, а; стрелка в кружке указывает направление возрастания потен­циала внутри источника ЭДС);

б) источник тока с током J - Е! R_B и параллельно с ним включенным сопротивлением Л_в (рис. 2.3, 6\ стрелки в кружке указывают положитель­ное направление тока источника тока, а небольшой разрыв между ними напоминает, что внутреннее сопротивление источника тока равно беско­нечности).

а б

Рис. 2.3

Ток в нагрузке (в сопротивлении R) для схем на рис. 2.3, а, б одина­ков: / = £/(/?+R_B), т. е. равен току в схеме на рис. 2.1, а. Для схемы рис. 2.3, а это следует из того, что при последовательном соединении зна­чения сопротивления R и R_e складываются. В схеме на рис. 2.3, б ток J = £/ R_B распределяется обратно пропорционально значениям сопротив­лений R и R_B двух параллельных ветвей. Ток в нагрузке R

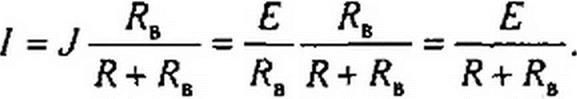
Каким из двух расчетных эквивалентов пользоваться, совершенно безразлично. В дальнейшем используется в основном первый эквивалент.

Обратим внимание на следующее:

1) источник ЭДС и источник тока — идеализированные источники, физически изготовить которые, строго говоря, невозможно;

2) схема на рис. 2.3, б эквивалентна схеме на рис. 2.3 а в отношении энергии, выделяющейся в сопротивлении нагрузки R, и не эквивалентна ей в отношении энергии, выделяющейся во внутреннем сопротивлении источника питания R_B;

3) идеальный источник ЭДС без последовательно соединенного с ним 7?_в нельзя заменить идеальным источником тока.

На примере схемы рис. 2.3 осуществим эквивалентный переход от схемы с источником тока к схеме с источником ЭДС. В схеме рис. 2.3, б источник тока дает ток J = 50 А. Шунтирующее его сопротивление /?_в=2Ом. Найти ЭДС эквивалентного источника ЭДС в схеме на рис. 2.3, а,

ЭДС E-JR_B = 100В. Следовательно, параметры эквивалентной схе­мы на рис. 2.3, а таковы: Е = 100 В, Я_в = 2 Ом.

§ 2.3 Неразветвленные и разветвленные электрические цепи. Электрические цепи подразделяют на неразветвленные и разветвленные. На рис. 2.1, а представлена схема простейшей неразветвленной цепи. Во всех элементах ее течет один и тот же ток. Простейшая разветвленная цепь изображена на рис. 2.4, а; в ней имеются три ветви и два узла.

а г

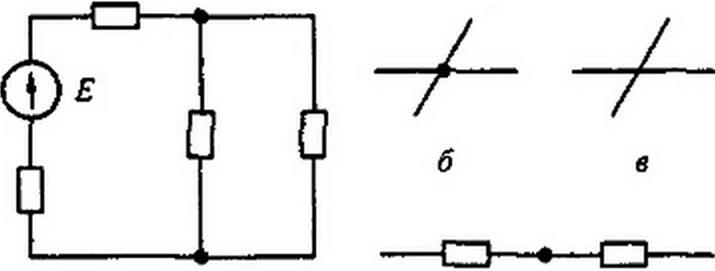
Рис. 2.4

В каждой ветви течет свой ток. Ветвь можно определить как участок цепи, образованный последовательно соединенными элементами (через которые течет одинаковый ток) и заключенный между двумя узлами. В свою очередь, узел — это точка цепи, в которой сходятся не менее трех ветвей. Если в месте пересечения двух линий на электрической схеме по­ставлена точка (рис. 2.4, б), то в этом месте есть электрическое соедине­ние двух линий, в противном случае (рис. 2.4, в) его нет.

Кроме термина «узел» иногда используют термин «устранимый узел». Под устранимым узлом понимают точку, в которой соединены два пос­ледовательных сопротивления (рис. 2.4, г). Этим понятием пользуются при введении данных в ЭВМ о значении и характере сопротивлений.

§ 2.4 Напряжение на участке цепи. Под напряжением на некотором участке электрической цепи понимают разность потенциалов между край­ними точками этого участка.

' На рис. 2.5 изображен участок цепи, крайние точ­

ки которого обозначены буквами а и Ь. Пусть ток I те- ------------------------------------------------------------- *• и_аъ

чет от точки а к точке Ъ (от более высокого потенциа- L • t—I • ла к более низкому). Следовательно, потенциал точки a r ь а (ф_о) выше потенциала точки b (ф_л) на значение, равное произведению тока I на сопротивление /?: ^ис' ‘

Ф, = ф_л + / Я.

В соответствии с определением напряжение между точками а и b

и_ак =<9а-<Н-

Следовательно,

V_ah=lR,

т. е. напряжение на сопротивлении равно произведению тока, протекаю­щего по сопротивлению, на значение этого сопротивления.

В электротехнике разность потенциалов на концах сопротивления называют либо напряжением на сопротивлении, либо падением напря­жения. В дальнейшем разность потенциалов на концах сопротивления, т. е. произведение / R, будем именовать падением напряжения.

Положительное направление падения напряжения на каком-либо уча­стке (направление отсчета этого напряжения), указываемое на рисунках стрелкой, совпадает с положительным направлением отсчета тока, про­текающего по данному сопротивлению.

В свою очередь, положительное направление отсчета тока / (ток — это скаляр алгеб­раического характера) совпадает с положительным направлением нормали к поперечному сечению проводника при вычислении тока по формуле / = J 8 dS, где 8 — плотность тока; dS — элемент площади поперечного сечения (подробнее см. § 20.1).

Рассмотрим вопрос о напряжении на участке цепи, содержащем не только сопротивление, но и ЭДС.

На рис. 2.6 показаны участки некоторых цепей, по которым протека­ет ток /. Найдем разность потенциалов (напряжение) между точками а и с для этих участков. По определению,

^=Фа-Фс- (2.1)

Выразим потенциал точки а через потенциал точки с. При перемеще­нии от точки с к точке b встречно направлению ЭДС Е (рис. 2.6, а) по­тенциал точки b оказывается ниже (меньше), чем потенциал точки с, на значение ЭДС Е: ф_А = ф_с. - Е. При перемещении от точки с к точке b согласно направлению ЭДС Е (см. рис. 2.6, б) потенциал точки b оказы­вается выше (больше), чем потенциал точки с, на значение ЭДС £: Фь = Фе + Е.

Так как по участку цепи без источника ЭДС ток течет от более высо­кого потенциала к более низкому, в обеих схемах рис. 2.6 потенциал точки а выше потенциала точки b на значение падения напряжения на сопро­тивлении R: ф_а = ф_А + / R.

б

Рис. 2.6

Таким образом, для рис. 2.6, а

фа =<Рс “^{£ + /}Я, и_ас = <р_а - ч>_с = 1 R - Е, (2.2)

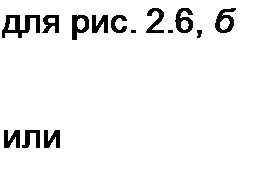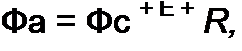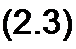
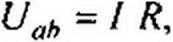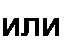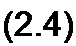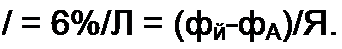= <р_о - = / Я + £•

Положительное направление напряжения U_QC показывают стрелкой от а к с. Согласно определению, U_ca = ф_с -ф_а, поэтому U_ea = -U_ac т. е. изменение чередования (последовательности) индексов равносильно изменению знака этого напряжения. Следовательно, напряжение может быть и положительной, и отрицательной величиной.

§ 2.5 Закон Ома для участка цепи, не содержащего источника ЭДС. Закон (правило) Ома для участка цепи, не содержащего источник ЭДС, устанавливает связь между током и напряжением на этом участке. Применительно к рис, 2.5

§ 2.6 Закон Ома для участка цепи, содержащего источник ЭДС. Обобщенный закон Ома. Закон (правило) Ома для участка цепи, содер­жащего источник ЭДС, позволяет найти ток этого участка по известной разности потенциалов (ф_<7'-ф_с) на концах участка цепи и имеющейся на этом участке ЭДС Е. Так, по уравнению (2.2) для схемы рис. 2.6, а

/ = (Ф_о-Ф_с+£)/Л = (^.4-£)//?;

4

-по уравнению (2.3) для схемы рис. 2.6, б

/ = (Ф_О ~ф_е-£)//? = ((7_0с-£)//?.

В общем случае

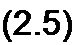_f _(Ч>_а-Ч>_с)±Е ₌ и_ас±Е
R R

Уравнение (2.5) математически выражает закон Ома для участка цепи, содержащего источник ЭДС; знак плюс перед Е соответствует рис. 2.6, а, знак минус — рис. 2.6, б. В частном случае при Е~ 0 урав­нение (2.5) переходит в уравнение (2.4).

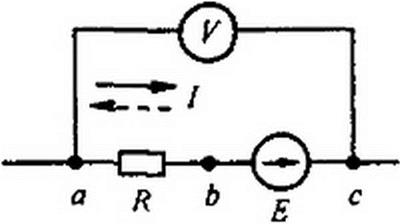
Пример 9. К зажимам а и с схемы рис. 2.7 подклю­чен вольтметр, имеющий очень большое, теоретически бесконечно большое сопротивление (следовательно, его подключение или отключение не влияет на режим рабо­ты цепи).

Если ток / = Ю А течет от точки а к точке с, то пока­зание вольтметра = -18 В; если этот ток течет от точ­ки с к точке а, то = -20 В. Определить сопротивле­ние Л и ЭДС Е.

Решение. В первом режиме

U'_a(. = -18 = -Е+/ Я = -Е + 10Я,

во втором

U' = -20 = -Е - / R = -Е -10 R.

Совместное решение дает £ = 19 В, R » 0,1 Ом.

§ 2.7 Законы Кирхгофа. Все электрические цепи подчиняются пер­вому и второму законам (правилам) Кирхгофа.

Первый закон Кирхгофа можно сформулировать двояко:

1) алгебраическая сумма токов, подтекающих к любому узлу схемы,

равна нулю;

2) сумма подтекающих к любому узлу токов равна сумме утекающих

от узла токов.

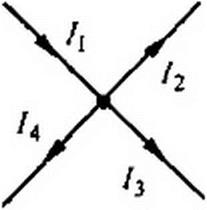
Применительно к рис. 2.8» если подтекающие к узлу токи считать положительными, а утекающие — отрица­тельными, то согласно первой формулировке 7] - /₂ - 7₃ - /₄ =0; согласно второй — 7, = /₂ + Л ⁺ Л ■

Физически первый закон Кирхгофа означает, что дви­жение зарядов в цепи происходит так, что ни в одном из узлов они не скапливаются.

Если мысленно рассечь любую схему произвольной плоскостью и все находящееся по одну сторону от нее рассматривать как некото­рый большой «узел», то алгебраическая сумма токов, входящих в этот «узел», будет равна нулю.

Второй закон Кирхгофа также можно сформулировать двояко:

1) алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура'.

(2.6)

(в каждую из сумм соответствующие слагаемые входят со знаком плюс, если они совпадают с направлением обхода контура, и со знаком минус, если они не совпадают с ним);

2) алгебраическая сумма напряжений (не падений напряжения'.) вдоль любого замкнутого контура равна нулю'.

(2.7)

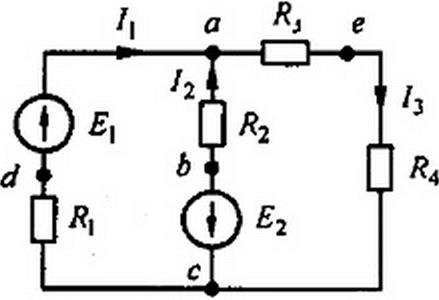
Для периферийного контура (рис. 2.9)

+ У* = 0.

Законы Кирхгофа справедливы для ли­нейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.

Сделаем два замечания:

1) запись уравнения по второму закону

Кирхгофа в форме (2.6) может быть полу­

чена, если обойти какой-либо контур неко-

торой схемы и записать выражение для потенциала произвольной точки этого контура через потенциал этой же точки (взяв ее за исходную при обходе) и падения напряжения и ЭДС;

2) при записи уравнений по второму закону Кирхгофа в форме (2.7)

напряжения участков цепи включают и падения напряжения участков, и имеющиеся на этих участках ЭДС.

3) 2.8. Составление уравнений для расчета токов в схемах с помо­щью законов Кирхгофа. Законы Кирхгофа используют для нахождения токов в ветвях схемы. Обозначим число всех ветвей схемы в, число ветвей, содержащих источники тока, — в_ит и число узлов у. В каждой ветви схемы течет свой ток. Так как токи в ветвях с источниками тока

известны, то число неизвестных токов равняется в-в_ит. Перед тем как составить уравнения, необходимо произвольно выбрать:

а) положительные направления токов в ветвях и обозначить их на схе­

ме;

б) положительные направления обхода контуров для составления урав­нений по второму закону Кирхгофа.

С целью единообразия рекомендуется для всех контуров положитель­ные направления обхода выбирать одинаковыми, например по часовой

стрелке.

Чтобы получить линейно независимые уравнения, по первому закону

Кирхгофа составляют уравнения, число которых равно числу узлов без

единицы, т. е. у- 1.

Уравнение для последнего у-го узла не составляют, так как оно со­впало бы с уравнением, полученным при суммировании уже составлен­ных уравнений для у - 1 узлов, поскольку в эту сумму входили бы дваж­ды и с противоположными знаками токи ветвей, не походящих к у-му узлу, а токи ветвей, подходящих к у-му узлу, входили бы в эту сумму со знаками, противоположными тем, с какими они вошли бы в уравнение

для у-го узла.

По второму закону Кирхгофа составляют уравнения, число которых равно числу ветвей без источников тока (в-в_ит), за вычетом уравнений, составленных по первому закону Кирхгофа, т. е.

(в-в_ит)-(у-1) = в-в_ит -? + !•

Составляя уравнения по второму закону Кирхгофа, следует охватить все ветви схемы, исключая лишь ветви с источниками тока.

Если попытаться составить уравнение по второму закону Кирхгофа в форме (2.6) для контура, в который входит источник тока, то в него вошли бы бесконечно большие слагаемые и оно не имело бы смысла.

При записи линейно независимых уравнений по второму закону Кирхгофа стремятся, чтобы в каждый новый контур, для которого состав­ляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в пре­дыдущие контуры, для которых уже записаны уравнения по второму закону Кирхгофа. Такие контуры условимся называть независимыми.

Требование, чтобы в каждый новый контур входила хотя бы одна новая ветвь, является достаточным, но не необходимым условием, а потому его не всегда выполняют. В таких условиях часть уравнений по второму закону Кирхгофа составляют для контуров, все ветви которых уже вошли в предыдущие контуры.

Пример 10. Найти токи в ветвях схемы на рис. 2.9. в которой Е\ =80 В, Е₂ = 64 В, /?] = 6 Ом, Я₂ - ⁴ Ом, Я₃ = 3 Ом, = I Ом.

Решение. Произвольно выбираем положительные направления тока в ветвях. В схеме на рис. 2.9 в = 3; в_ит =0; у-2.

Следовательно, по первому закону Кирхгофа, можно составить только одно уравне­ние:

/i + /₂ = /j. (2.8)

Нетрудно убедиться, что для второго узла получили бы аналогичное уравнение. По второму закону Кирхгофа составим (в-в_ит)-(у-1) = 3-0-(2-1) = 2 уравнения. Поло­жительные направления обхода контуров выбираем по часовой стрелке.

Для контура Е_ХЕ_{Я₂Е₂

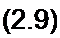/₂ /?2 + /₃ (Я₃ + Я₄) - -£₂.

Знак плюс перед взят потому, что направление тока совпадает с направлением обхода контура; знак минус перед /₂ Л₂ — потому, что направление /₂ встречно обходу контура.

Для контура £₂Л₂Л₃/?₄

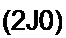/₂ Я₂ -/₃ (/?₃ + /?₄) = -Е₂.

Совместное решение уравнений (2.8Н2. Ю) дает /) = 14 А, /₂ = -15А, /₃ = -1А.

Поскольку положительные направления токов выбирают произвольно, в результате расчета какой-либо один или несколько токов могут оказаться отрицательными. В рассмот­ренном примере отрицательными оказались токи /₂ и /₃, что следует понимать так: на­правления токов /₂ и /₃ не совпадают с направлениями, принятыми для них на рис. 2.9 за положительные, г. с. в действительности токи /₂ и /₃ протекают в обратном направ­лении.

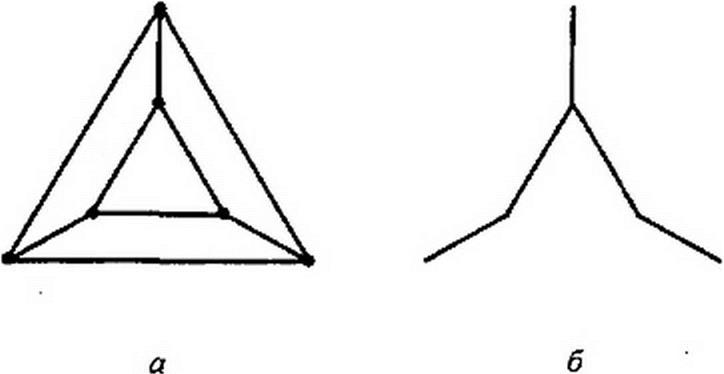
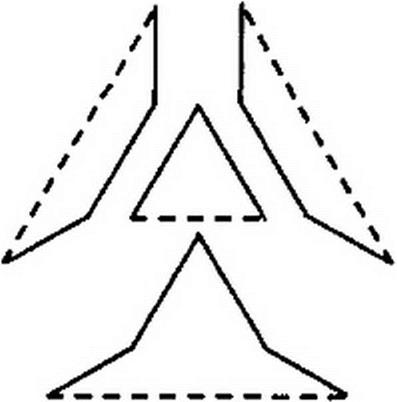
Для выбора контура таким образом, чтобы в каждый из них входило по одной ветви, не входящей в остальные контуры, используют понятие дерева. Под деревом понимают совокупность ветвей, касающихся всех узлов, но не образующих ни одного замкнутого контура. Из одной и той же схемы можно образовать несколько деревьев. При составле­нии системы уравнений по второму закону Кирхгофа можно взять любое дерево из воз­можных. Одно из возможных деревьев схемы рис. 2.10, а изображено на рис. 2.10, б, а на рис. 2.10, в — четыре независимых контура, в каждый из которых входит по одной ветви, показанной штриховой линией, не входящей в остальные. Более подробно о топологии электрических схем см. §2.31-2.35 и П1.5-П1.10.

§ 2.9 Заземление одной точки схемы. Заземление любой точки схе­мы свидетельствует о том, что потенциал этой точки принят равным нулю. При этом токораспределение в схеме не изменяется, так как ника­ких новых ветвей, по которым могли бы протекать токи, не образуется. Иначе будет, если заземлить две или большее число точек схемы, имеющих различные потенциалы. В этом случае через землю (любую проводящую среду) образуются дополнительные ветви, сама схема становится отличной от исходной и токораспределение в ней меняется.

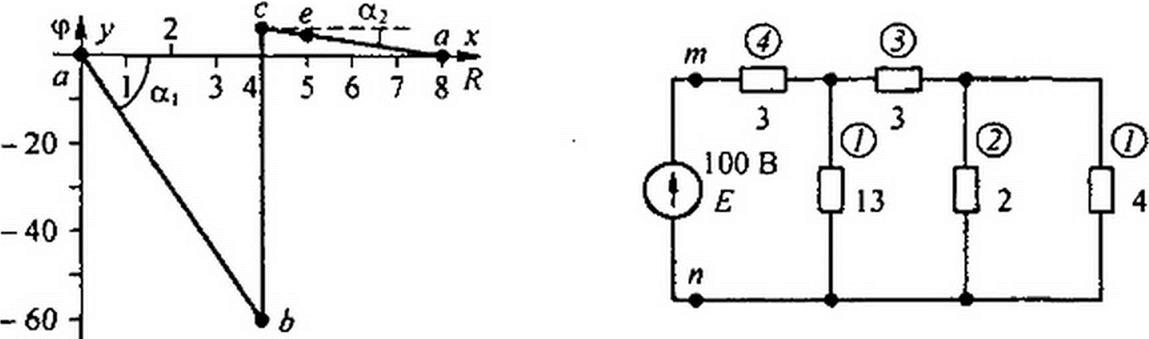
§ 2.10 Потенциальная диаграмма. Под потенциальной диаграммой понимают график распределения потенциала вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают со­противления вдоль контура, начиная с какой-либо произвольной точки, по оси ординат — потенциалы. Каждой точке участка цепи или замкну­того контура соответствует своя точка на потенциальной диаграмме.

Рассмотрим последовательность построения потенциальной диаграм­мы по данным примера 2.

Потенциал точки b: ф/, = ф_Л + /₂ 4 = ф_о -60--60 В; ее координаты: х = 4, у- -60. Потенциал точки с: ц>_с = ф_Л + £₂ = ⁴ ее координаты: х = 4, у = 4. Потенциал точки е: Ф_е = ф_с + /₃ Л₄ = 4 -1^х I = 3 В; ее координаты: х ~ 5, у = 3.

Тангенс угла а, наклона прямой <х_аЬ к оси абсцисс пропорционален току /₂, а тан­генс угла а₂ наклона прямой се — току /₃; tga = /—, где т_г, т₉— масштабы по осям хи у. ^т<>

Обратим внимание на различие в знаках, с которыми входит падение напряжения / R при определении потенциала какой-либо точки схемы через потенциал исходной точки и при составлении уравнений по второму закону Кирхгофа. При вычислении потенциала последующей точки через потенциал предыдущей / R берут со знаком минус, если пере­мещение по сопротивлению R совпадает по направлению с током, тогда как при сос­тавлении уравнений по второму закону Кирхгофа / R некоторого участка цепи берут в сумме £ / Я со знаком плюс, если обход этого участка совпадает с направлением тока 1 на нем.

§ 2.11 Энергетический баланс в электрических цепях. При проте­кании токов по сопротивлениям в последних выделяется теплота. На ос­новании закона сохранения энергии количество теплоты, выделяющееся в единицу времени в сопротивлениях схемы, должно равняться энергии, доставляемой за то же время источником питания.

Если направление тока /, протекающего через источник ЭДС Е, совпадает с направлением ЭДС, то источник ЭДС доставляет в цепь энер­гию в единицу времени (мощность), равную Е /, и произведение Е I входит в уравнение энергетического баланса с положительным знаком.

Если же направление тока / встречно направлению ЭДС Е, то источ­ник ЭДС не поставляет энергию, а потребляет ее (например, заряжается аккумулятор), и произведение Е I войдет в уравнение энергетического баланса с отрицательным знаком.

Уравнение энергетического баланса при питании только от источни­ков ЭДС имеет вид

£l²R = £EI.

Когда схема питается не только от источников ЭДС, но и от источни­ков тока, т. е. к отдельным узлам схемы подтекают и от них утекают токи источников тока, при составлении уравнения энергетического баланса необходимо учесть и энергию, доставляемую источниками тока.

Допустим, что к узлу а схемы подтекает ток J от источника тока, а от узла b этот ток утекает. Доставляемая источником тока мощность равна U_oh Л

Напряжение U_ah и токи в ветвях схемы должны быть подсчитаны с учетом тока, подтекающего от источника тока. Последнее проще всего сделать по методу узловых потенциалов (см. § 2.22). Общий вид уравне­ния энергетического баланса:

х/^г R = Y.EI ₊ Y.U_akJ.

Для практических расчетов электрических цепей разработаны мето­ды, более экономичные в смысле затраты времени и труда, чем метод расчета цепей по законам Кирхгофа. Рассмотрим эти методы.

§ 2.12 Метод пропорциональных величин. Согласно методу про­порциональных величин, в самой удаленной от источника ЭДС ветви схемы (исходной ветви) произвольно задаемся некоторым током, напри­мер током в 1 А. Далее, продвигаясь к входным зажимам, находим токи в ветвях и напряжения на различных участках схемы. В результате рас­чета получим значение напряжения U_mn схемы и токов в ветвях, если в исходной ветви протекает ток в 1 А.

Так как найденное значение напряжения U_mn в общем случае окажет­ся не равным ЭДС источника, то следует во всех ветвях изменить токи, умножив их на коэффициент, равный отношению ЭДС источника к най­денному значению напряжения в начале схемы.

Метод пропорциональных величин, если рассматривать его обособ­ленно от других методов, применим для расчета цепей, состоящих толь­ко из последовательно и параллельно соединенных сопротивлений и при наличии в схеме одного источника. Однако этот метод можно использо­вать и совместно с другими методами (преобразование треугольника в звезду, метод наложения и т. п.), которые рассмотрены далее.

Пример 12. Найти токи в ветвях схемы (рис. 2.11, б) методом пропорциональных ве­личин. Сопротивления схемы даны в омах.

Решение. Задаемся током в ветви с сопротивлением 4 Ом, равным 1 А, и подсчиты­ваем токи в остальных ветвях (числовые значения токов обведены на рисунке кружками). Напряжение между точками тип равно 1-4 + 3-34-4-3 = 25В. Так как ЭДС £ = 100 В, все токи следует умножить на коэффициент к ~ 100/25 = 4.

§ 2.13 Метод контурных токов. При расчете методом контурных токов полагают, что в каждом независимом контуре схемы течет свой кон­турный ток. Уравнения составляют относительно контурных токов, пос­ле чего через них определяют токи ветвей.

Таким образом, метод контурных токов можно определить как ме­тод расчета, в котором за искомые принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить для схемы по второму закону Кирхгофа.

Следовательно, метод контурных токов более экономен при вычисли­тельной работе, чем метод на основе законов Кирхгофа (в нем меньше чибло уравнений).

Вывод основных расчетных уравнений приведем применительно к схеме с двумя независимыми контурами (рис. 2.12). Положим, что в левом контуре по часовой стрелке течет контурный ток /_и, а в правой

я, я?

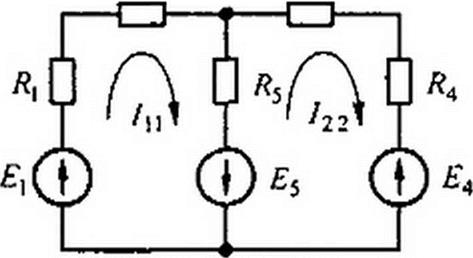
Рис. 2.12

(также по часовой стрелке) — контурный ток /₂2- Д'™ каждого контура составим уравнения по второ.му закону Кирхгофа. При этом учтем, что по смежной ветви (с сопротивлением /?₅) течет сверху вниз ток /|]-/₂2- Направления обхода контуров примем также по часовой стрелке.

Для первого контура

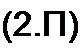
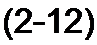(/?! + /?2) Л1 ⁺ ^5 (А ! Л₂) " ^1 ⁺ ^5

или

(/?] + /?2 ⁺ £5) Al ⁺(~^s) ^22 “ £1 ⁺ £$•

Для второго контура

(/, । - /₂2) +(^з + Яд) Лг = ~^Е5 "^4

или

(—Л₅) /] | + /?4 + К₅) /₂2 - ~^Е5 ~~ ^Е4-

В уравнении (2.12) множитель при токе /_н, являющийся суммой сопротивлений первого контура, обозначим через множитель при токе /₂₂ (сопротивление смежной ветви, взятое со знаком минус) — через Т?|₂.

Перепишем эти уравнения следующим образом:

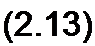^E ll Ai ⁺ ^12 ^22 ~ /?21 /|| + ^22 /22 = ^22-

Здесь

/?1 ] = /?| + /?, + Я₅; Ец = Е_} + Е$', /?₁₂ ⁼ Я₂₁ -

/?22 ~ + Т?5 j Е22------- Е$ — Е₅,

где /?ц — полное, или собственное, сопротивление первого контура; /?₁₂ — сопротивление смежной ветви между первым и вторым конту- рами, взятое со знаком минус; £_н — контурная ЭДС первого контура, равная алгебраической сумме ЭДС этого контура (в нее со знаком плюс входят те ЭДС, направления которых совпадают с направлением обхода контура); R₂₂ — полное, или собственное, сопротивление второго контура; /?₂| — сопротивление смежной ветви между первым и вторым контурами, взятое со знаком минус; Е₂₂ — контурная ЭДС второго кон­тура.

В общем случае можно сказать, что сопротивление смежной ветви между А- и m-кон­турами входит в уравнение со знаком минус, если направления контурных токов 1_кк и /_тпУ вдоль этой ветви встречны, и со знаком плюс, если направления этих токов согласны.

Если в схеме больше двух контуров, например три, то система урав­нений выглядит следующим образом:

Л) ⁺ Я|2 ^22 ⁺ *13 Лз - £ц*>
1 *21 Л1 ⁺ *22 Лг ⁺ *23 Лз = *22’
.*31 Al ⁺ *32 ^22 ⁺ *33 Лз ~ *33»

или в матричной форме

[*][/] = [^];

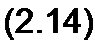
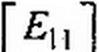
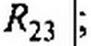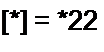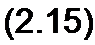*11 *12

*31 *32

Рекомендуется для единообразия в знаках сопротивлений с разными индексами все контурные токи направлять в одну и ту же сторону, на­пример по часовой стрелке.

В результате решения системы уравнений какой-либо один или несколько контурных токов могут оказаться отрицательными.

В ветвях, не являющихся смежными между соседними контурами (например, в ветви с сопротивлениями Я₂ на рис. 2.12), найденный контурный ток является действительным током ветви. В смежных ветвях через контурные токи определяют токи ветвей. Например, в ветви с со­противлением Т?₅ протекающий сверху вниз ток равен разности /₍₁ - /₂₂.

Если в электрической цепи имеется п независимых контуров, то чис­ло уравнений тоже равно п.

Общее решение системы п уравнений относительно тока :

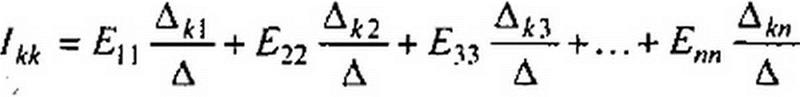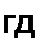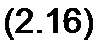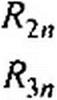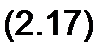^п\ *»2 *«3 ••• &пп

есть определитель системы.

Алгебраическое дополнение Д_ы получено из определителя Д путем вычеркивания А-го столбца и w-й строки и умножения полученного оп­ределителя на

Если из левого верхнего угла определителя провести диагональ в его правый нижний угол (главная диагональ) и учесть, что R_km = R_mk, то можно убедиться в том, что определитель делится на две части, являю­щиеся зеркальным отображением одна другой. Это свойство определи­теля называют симметрией относительно главной диагонали. В силу симметрии определителя относительно главной диагонали Ь_кт = ^_тк.

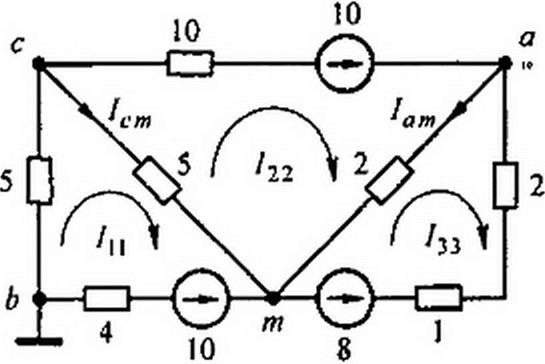
Пример 13. Найти токи в схеме (рис. 2.13) методом контурных токов. Числовые значения сопротивлений в омах и ЭДС в вольтах указа­ны на рисунке.

Решение. Выберем направления всех контурных токов /_н, /₂₂, /₃₃ по часовой стрелке. Определяем:

/?) । = 5 +5+ 4 = 14О.м;

/?₂₂ — 5 + 10 + 2 ⁼ 17 Ом; /?₃₃ = 2 + 2 +1 = 5 Ом;

«12 = /?2| = -5 0м;

/?23 ~ ^{= —}Ом; £j । = -10 В;

Е24 ^— 10 В; E_i3 ^{= _}8В. Записываем систему уравнений:

|4/„-5/_и = -10;

-5/„ + 17 1₂₂ -21„ = 10;

^— 2 + 5 /₃₃ = - 8.

Определитель системы

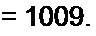0

-2
5

Подсчитаем контурные токи

-10 -5 0

10 17 -2

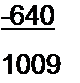
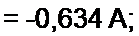-8 2 5

А₂ = 0,224 А; /₃₃ = -1,51А.

Ток в ветви ст 1_ст = /, , - /₂₂ = -0,63 - 0,224 = -0,86 А.

Ток в ветви am i_an, = /₂₂ - /₃₃ = 0,224 + 1,51 = 1,734 А.

Формула (2.16) в ряде параграфов используется в качестве исходной при рассмотрении таких важных вопросов теории линейных электриче­ских цепей, как определение входных и взаимных проводимостей ветвей, принцип взаимности, метод наложения и линейные соотношения в элек­трических цепях.

Составлению уравнений по методу контурных токов для схем с источниками тока присуши некоторые особенности. В этом случае по-

лагаем, что каждая ветвь с источником тока входит в контур, замыкаю­щийся через ветви с источниками ЭДС и сопротивлениями, и что токи в этих контурах известны и равны токам соответствующих источников тока. Уравнения составляют лишь для контуров с неизвестными контурными токами. Если для схемы на рис. 2.14, а принять, что контурный ток

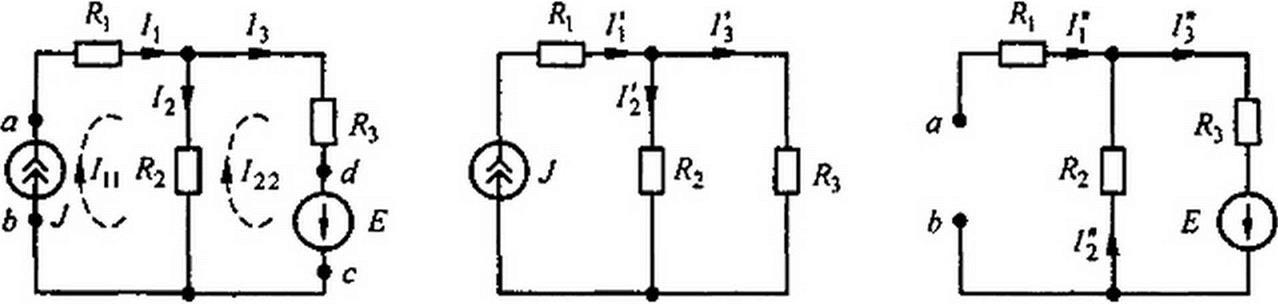7ц = J течет согласно направлению часовой стрелки по первой и вто­рой ветвям, а контурный ток /₂2 ~ h замыкается также по часовой стрел­ке по второй и третьей ветвям, то, согласно методу контурных токов, по­лучим только одно уравнение с неизвестным током 1₂₂^:

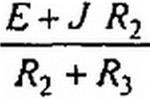
(Я₂ + Я₃)/₂₂-/?₂ J = E.

и ток второй ветви /₂ = /ц ~/₂₂.

§ 2.14 Принцип наложения я метод наложения. Чтобы составить общее выражение для тока в А-ветви сложной схемы, составим уравне­ния по методу контурных токов, выбрав контуры так, чтобы А-ветвь вхо­дила только в один А-контур (это всегда возможно). Тогда согласно (2.16) ток в А-ветви будет равен контурному току 1_кк. Каждое слагаемое пра­вой части (2.16) представляет собой ток, вызванный в А-ветви соответст­вующей контурной ЭДС. Например, £_и А_к1/ Д есть составляющая тока А-ветви, вызванная контурной ЭДС Е_и. Каждую из контурных ЭДС мож­но выразить через ЭДС ветвей Е_]у Е₂, Е₃,..., Е_к,..., Е_пУ сгруппировать коэффициенты при этих ЭДС и получить выражение следующего вида:

At = ^Е\ Ski + ^2 Ski ^{+ Е}з 8кз+- ^{+ Е}к Zkk+^En gk>r (^2J8)

Если контуры выбраны таким образом, что какая-либо из ЭДС, напри­мер Е_т, входит только в один /n-контур, а в другие контуры не входит, ТО Skm ~ ^кт !

Уравнение (2.18) выражает собой принцип наложения.

Принцип наложения формулируется следующим образом: ток в к-ветви равен алгебраической сумме токов, вызываемых каждой из ЭДС схемы в отдельности. Этот принцип справедлив для всех линейных элек­трических цепей.