Коэффициент пропорциональности Л/(Гн) называют взаимной индук­тивностью

Дата: 2025-06-02; Просмотры: 11

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

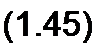Она зависит от взаимного расположения, числа витков, геометриче­ских размеров контуров (катушек) и от магнитной проницаемости ц_а сер­дечников, на которых они намотаны. Если ц_а = const, то от величины токов Л/ не зависит.

Явлением взаимоиндукции называют наведение ЭДС в одном контуре при изменении тока в другом. Наводимую ЭДС называют ЭДС взаимо­индукции и обозначают е_м. Для рис. 1.13 полная ЭДС, наводимая в пер­вом контуре,

е_|=-4(Ч-₁±Т_2|) = -4(Д1',±Л//₂) =
at dt

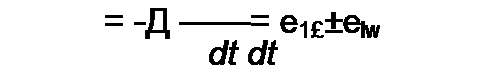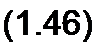и во втором

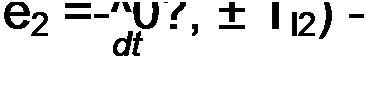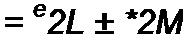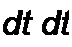В формулах (1.46) и (1.47) принято, что М > 0. В то же время в лите­ратуре можно встретиться с тем, что знак минус у е_м в этих формулах относят не к ЭДС взаимоиндукции, а к М, т. е. записывают формулы (1.46) и (1.41) в виде

^е1 - ^e \f. ^{+ е}\м ^{И е}2 ^{= е}21. ^{+ в}2М .

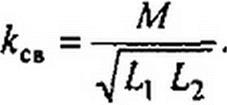Под коэффициентом связи двух магнитосвязанных катушек пони­мают отношение М к квадратному корню из произведения L₂ этих катушек

(1.48)

Всегда А_св < 1; Л_св = 1, если весь магнитный поток, создаваемый первой катушкой, пронизывает и вторую, а весь поток, генерируемый второй катушкой, пронизывает и первую.

Магнитная энергия двух магнитосвязанных катушек с токами и /₂ равна

/₂. (1.49)

Знак «+» относится к согласному, «-» — к встречному направлению потоков.

Пример 6. На сердечнике примера 4, кроме катушки с числом витков = 1000, рав­номерно намотана и вторая катушка w₂ - 500. Определим М между катушками.

Решение. Весь поток Ф, создаваемый в сердечнике первой катушкой, пронизыва­ет и вторую. Поэтому

У И₀ w, w₂ ^In-y-

М = — ------------------------------ — = 0,0655 Гн.

Ц 2п

Пример 7..Определить магнитную энергию, запасаемую в магнитном поле двух кату­шек примера 6, если по первой катушке течет ток Л = 1 А, по второй — ток /₂ =0,5 А. Магнитные потоки направлены согласно.

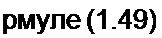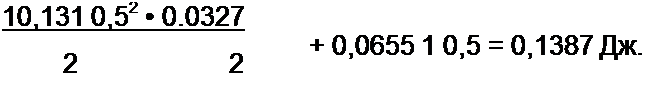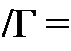Решение. По формуле (1.44), заменив в ней w'_t на w₂, определяем L₂ = 0,0327 Гн.

Пример 8. По первой катушке примера 7 течет ток /_ь изменяющийся во времени в соответствии с рис. 1.13, 6. Вторая катушка разомкнута. Построить кривые ЭДС самоин­дукции e_it и ЭДС взаимоиндукции е_2М (время дано в мс).

Решение. График е_}[ (рис. 1.13, е) строим по формуле

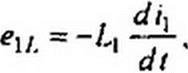график е_2М (рис. 1.13, г) — по

at

§ 1.7 Схемы замещения реальных электротехнических устройств. В элементах реальных электротехнических устройств (электрических цепях) происходят достаточно сложные процессы протекания токов про­водимости, токов смешения, выделения тепловой энергии, наведения ЭДС, накопления и перераспределения энергии электрического и магнит­ного полей и т. п. Для того чтобы можно было математически описать эти процессы, в теории цепей пользуются расчетными схемами (схемами замещения), вводя в них резистивные, индуктивные и емкостные элемен­ты. С помощью резистивного элемента учитывают выделение теплоты в реальном элементе; с помощью индуктивного элемента — наведение ЭДС и накопление энергии в магнитном поле; с помощью емкостного эле­мента — протекание токов смещения и накопление энергии в электри­ческом поле.

Каждый элемент реальной электрической цепи на схеме замещения можно представить той или иной совокупностью идеализированных схем­ных элементов.

Так, резистор для низких частот можно представить одним резистив­ным элементом R (рис. 1.14, а). Для высоких частот тот же резистор дол­

жен быть представлен уже иной схемой (рис. 1.14, б). В ней малая (паразитная) индуктивность L_n учитывает магнит­ный поток, сцепленный с резистором, а малая паразитная емкость С_п учитыва­ет протекание тока смещения между зажимами резистора. Конденсатор на низких частотах замещают одним емко­стным элементом (рис. 1.14, а), а на вы-

соких частотах конденсатор представля­ют схемой, где резистор R_n учитывает потери в неидеальном диэлектрике конденсатора, a L_n — паразитная индуктивность подводящих контактов (рис. 1.14, г).

Индуктивную катушку в первом приближении можно представить одним индуктивным элементом L (рис. 1.14,6). Более полная схема за­мещения может быть представлена на рис. 1.14, е). В ней /?_п учитывает тепловые потери в сопротивлении обмотки и в сердечнике, на котором она намотана, а паразитная емкость С_п учитывает токи смещения меж­ду витками катушки.

Обобщенно можно сказать, что при составлении схемы замещения ре­

альных элементов цепи и цепи в целом в нее входят те идеализированные схемные элементы, с помощью которых описываются основные процес­сы в реальных элементах цепи, а процессами, являющимися относительно второстепенными в этих элементах для рассматриваемой полосы частот и амплитуд воздействий, обычно пренебрегают. Реальную электрическую

цепь, представленную в виде совокупности идеализированных схемных элементов, в дальнейшем будем называть схемой замещения электричес­кой цепи или, короче, схемой электрической цепи.

Если можно считать, что напряжение и ток на всех элементах реаль­ной цепи не зависят от пространственных координат, то такую цепь называют цепью с сосредоточенными параметрами^ если зависят — цепью с распределенными параметрами.

Процессы в цепи с сосредоточенными параметрами описывают алгеб­раическими или обыкновенными дифференциальными уравнениями; про­цессы в цепях с распределенными параметрами описывают уравнениями в частных производных. Дальнейшее подразделение типов цепей будет дано по ходу изложения. Соответствие расчетной модели реальной элект­рической цепи проверяют, сопоставляя расчет с экспериментом. Если расчетные данные недостаточно сходятся с экспериментом, модель уточ­няют.

В курсе ТОЭ используют общие физические принципы, формирующие диалектическое мышление, такие, как принцип симметрии, принцип минимума энергии, закон сохранения заряда, принцип непрерывности маг­нитного потока. При выполнении лабораторных работ студент ощущает реальность явлений, о которых шла речь в теории. Методы расчета элект­рических цепей можно излагать по крайней мере двумя способами. Соглас­но первому их излагают одновременно с теорией электрических цепей си­нусоидального тока. Согласно второму методы расчета рассматривают по отношению к резистивным цепям постоянного тока, а затем эти методы распространяют на цепи синусоидального тока. Второй способ, с нашей точки зрения, методически более целесообразен — материал, разделенный на две самостоятельные части, усваивается легче и прочнее. Кроме того, студент приобретает навык в расчете цепей постоянного тока, область применения которых достаточно широка.