Закон полного тока в интегральной форме для любой среды принято записывать в виде
Л. А. Бессонов
Теоретические основы электротехники
ЭЛЕКТРИЧЕСКИЕ
ЦЕПИ
УЧЕБНИК ДЛЯ БАКАЛАВРОВ
12-е издание, исправленное и дополненное
Допущено Министерством образования Российской Федерации
в качестве учебника для студентов высших учебных заведений,
обучающихся по направлениям подготовки дипломированных
специалистов «Электротехника, электромеханика и электротехнологии»,
«Электроэнергетика», «Приборостроение»

2013
Москва ■ Юрайт ■ 2016
УДК 621.3.013(078.5)
ББК 31.21я73
ББ Б53
Автор:
Бессонов Лев Алексеевич — доктор технических наук, профессор, с 1955 по 2000 г. заведовал кафедрой «Теоретические основы электротехники» Московского государственного института радиотехники, электроники и автоматики (технический университет).
Рецензенты:
Миронов В. Г. — доктор технических наук, профессор, заслуженный деятель науки РФ;
Бутырин П. А. — доктор технических наук, профессор, член-корреспондент Российской академии наук.
Бессонов, Л. А.
Б53 Теоретические основы электротехники. Электрические цепи : учебник для бакалавров / Л. А. Бессонов. — 12-е изд., исправ. и доп. — М. : Издательство Юрайт, 2016. — 701 с. — Серия : Бакалавр. Углубленный курс.
ISBN 978-5-9916-3210-2
Рассмотрены традиционные и новые вопросы теории линейных и нелинейных электрических цепей. К традиционным относятся методы расчета токов и напряжений при постоянных, синусоидальных, импульсных и других видах воздействий, теория двух- и четырехполюсников, электрические фильтры, электрические и магнитные линии с распределенными параметрами, расчет переходных процессов классическим, операторным методами, методом интеграла Дюамеля, обобщенных функций, методом пространства состояний, преобразования Фурье, аналоговый и цифровой сигналы, основы теории сигналов, цифровые фильтры, имитированные элементы и их применение, преобразование Брутона, преобразование Гильберта, установившиеся и переходные процессы в нелинейных электрических цепях, устойчивость различных видов движений, субгармонические колебания.
К числу новых вопросов, включенных в курс, относятся физические причины, условия возникновения и каналы действия нелинейной, неявно выраженной обратной связи в нелинейных электрических цепях переменного тока, приводящие к возникновению в них колебаний, получивших название «странные аттракторы», метод расчета установившегося режима работы обобщенной цепи переменного тока с учетом высших гармоник, использующий принцип диакоптики, макрометод расчета переходных процессов в мостовой выпрямительной схеме с предвключен- ным сопротивлением в цепи переменного тока, магнитотранзисторный генератор напряжения типа меандра, основные положения вейвлет-преобразования сигналов, новый подход к составлению уравнений для приращений при исследовании устойчивости периодических процессов в нелинейных цепях с источником синусоидальной ЭДС, позволяющей простым путем свести уравнение для приращений к уравнению Матье, и ряд других новых вопросов.
По всем вопросам курса даны примеры с подробными решениями. В конце каждой главы — вопросы и задачи для самопроверки. Соответствует Федеральному государственному образовательному стандарту высшего профессионального образования третьего поколения.
Для студентов и преподавателей высших учебных заведений, инженеров, аспирантов и научных работников электротехнических и близких к ним специальностей.
УДК 621.3.013(078.5)
ББК 31.21я73
 © Бессонов Л. А., 2011
© Бессонов Л. А., 2011
© ООО «Издательство Юрайт», 2016
ПРЕДИСЛОВИЕ
Двенадцатое исправленное и дополненное издание учебника по курсу «Теоретические основы электротехники» Л. А. Бессонова образуют два тома. Первый том — «Электрические цепи», второй — «Электромагнитное поле». Курс ТОЭ является базовым курсом, на который опираются многие профилирующие дисциплины высших технических учебных заведений.
Учебник соответствует программе курса ТОЭ, утвержденной Министерством образования и науки Российской Федерации. В него включены самые последние разработки по теории цепей и по теории электромагнитного поля.
В учебник «Электрические цепи» кроме традиционных вопросов теории электрических цепей — свойств цепей, их топологии, методов расчета токов и напряжений при постоянных, синусоидальных, периодических несинусоидальных, многофазных, импульсных воздействиях, теории двухполюсников, четырехполюсников и многополюсников, резонансных явлений, частотных характеристик, цепей со взаимоиндукцией, теории графов, электрических фильтров k, т и RC-типа, линий с распределенными параметрами, различных методов расчета переходных процессов (классического, операторного, интеграла Дюамеля по мгновенным значениям величин и по огибающим, метода пространства состояний, метода обобщенных функций), частотных преобразований цепей, преобразований Фурье, цепей с переменными во времени параметрами, включены следующие новые вопросы: свойства нелинейных цепей постоянного и переменного тока и методы их расчета в установившихся и переходных процессах работы, вопросы устойчивости автоколебаний и периодических процессов под воздействием периодических вынуждающих сил, субгармонические колебания, фазовая плоскость, случайные процессы.
В книге рассмотрены также основы теории сигналов, аналоговый, цифровой и аналитический сигналы, преобразования Фурье цифровых сигналов, дискретная свертка, цифровые фильтры, обобщенные формулы для расчета переходных процессов в линиях с распределенными параметрами при произвольных сопротивлениях генератора и нагрузки и многократных отражениях, магнитные линии с распределенными параметрами, имитированные элементы электрических цепей и их применение, преобразование Гильберта, преобразование Брутона, основы устойчивости сложных типов движений, электромоделирование, переходные процессы в цепях с управляемыми источниками напряжения и тока с учетом их нелинейных и частотных свойств, в цепях с термисторами, в электромеханических системах, передаточные функции активных RC-фильтров и методика их расчета.
Кроме перечисленных выше в настоящем, двенадцатом издании рассмотрены следующие новые вопросы, отсутствовавшие во всех предыдущих изданиях учебника: работа часто встречающихся на практике мостовых выпрямительных схем с элементами RL и RC в цепи выпрямленного тока, анализ работы магнитотранзисторного генератора прямоугольного напряжения в виде меандра, теория линейного активного автономного четырехполюсника применена к расчету нелинейных цепей с двумя нелинейными элементами в двух удаленных друг от друга ветвях схемы; объяснено, почему в нелинейных электрических цепях переменного тока возможно возникновение большого числа различных типов движений; для цепи с двумя разнохарактерными нелинейностями выведены формулы для определения условий перехода от предыдущих типов движений к последующим. Рассмотрены физические причины, условия возникновения и каналы действия внутренней нелинейной, неявно выраженной обратной связи, приводящей к автомодуляции и хаосу (к странным аттракторам) в нелинейных электрических цепях переменного тока.
Причины возникновения этих явлений и каналы действия внутренней нелинейной обратной связи пояснены на конкретных схемах. Странные аттракторы в нелинейных цепях переменного тока сопоставлены с автоколебаниями в нелинейных цепях с источниками постоянной ЭДС, показано, в чем между ними есть сходство и в чем различие, рассмотрен математический критерий Фейгенбаума возникновения хаоса в нелинейных недиссипативных системах, конвергентные и неконвергентные электрические цепи, дуальные нелинейные цепи. Предложен макрометод расчета переходных процессов в мостовой выпрямительной схеме с предвключенным сопротивлением в цепи переменного тока. Изложен аналитический метод расчета нелинейных цепей переменного тока, позволяющий, используя принцип диакоптики, проводить расчет токов и напряжений в обобщенной цепи с учетом высших гармоник. В раздел синтеза цепей включен синтез четырехполюсников по передаточной функции с помощью схем с операционным усилителем в цепи обратной связи. Раздел теории сигналов дополнен основными положениями вейвлет- преобразования сигналов. Раздел исследования устойчивости различных видов движений дополнен методом исследования устойчивости периодических процессов в линейных электрических цепях с переменными во времени параметрами, находящихся под воздействием синусоидальной ЭДС, основанным на сведении уравнений для приращений к уравнению Матье. Предложен и иллюстрирован примером новый подход к составлению уравнений для приращений при исследовании устойчивости периодических процессов в нелинейных цепях с источником синусоидальной ЭДС, позволяющий учесть влияние на устойчивость четных гармоник и простым и удобным путем привести уравнение для приращений к уравнению Матье. Рассмотрен метод исследования устойчивости работы рекурсивных цифровых фильтров.
Как и в предыдущих изданиях, весь материал учебника разделен на обязательный для изучения студентами всех специальностей, в учебном плане которых имеется курс ТОЭ или родственный курс с несколько иным названием (этот материал является ядром курса и набран нормальным шрифтом), и на специальный, или дополнительный, который в неодинаковой степени необходим студентам различных специальностей (выделен петитом). Какую часть специального материала рекомендуется изучить студенту, зависит от специфики института, факультета и кафедры.
Известно, что теория усваивается легче и прочнее, когда она по ходу изложения сопровождается решением задач на рассматриваемые темы. Исходя из этого, во всех главах и приложениях автор приводит решения с пояснениями достаточно полных комплектов задач по всем основным вопросам всех глав и приложений. Кроме того, в конце каждой главы приведены вопросы и задачи для самопроверки.
После изучения данного курса студенты должны:
знать
— как традиционные, так и новые вопросы теории линейных и нелинейных цепей;
— основы теории сигналов;
— работу мостовых выпрямительных схем с элементами RL и RC в цепи выпрямленного тока;
— синтез электрических цепей;
— теорию линейного активного автономного четырехполюсника;
— разновидности магнитных цепей и построение их вебер- амперных характеристик;
— принципы работы биполярного и полевого транзисторов;
— характеристику направленных и ненаправленных графов;
— дискретные сигналы;
— частотные преобразования и преобразования цифровых сигналов;
уметь
— принимать условия для определения характеристик электрических и магнитных цепей;
— использовать методы анализа и расчета для различных процессов в целях постоянного и переменного итога и построения схем электрических цепей;
владеть
— навыками решения задач по всем основным темам теории электрических цепей.
Выражаю благодарность официальному рецензенту книги доктору технических наук, профессору Московского энергетического института (государственный университет) В. Г. Миронову за обстоятельную рецензию и полезные замечания, способствовавшие улучшению книги. Благодарю моих товарищей по работе в Московском государственном институте радиотехники, электроники и автоматики (технический университет) кандидата технических наук, доцента А. В. Штыкова и доцента С. Э. Расовскую за помощь в подготовке книги к изданию и за высказанные ими замечания по рукописи, учтенные мной.
Автор
Гчава первая
ОСНОВНЫЕ ПОЛОЖЕНИЯ
ТЕОРИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
И ИХ ПРИМЕНЕНИЕ
К ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
§ 1.1. Электромагнитное поле как вид материи. Под электромагнитным полем понимают вид материи, характеризующийся совокупностью взаимосвязанных и взаимообусловливающих друг друга электрического и магнитного полей. Электромагнитное поле может существовать при отсутствии другого вида материи — вещества, характеризуется непрерывным распределением в пространстве (электромагнитная волна в вакууме) и может проявлять дискретную структуру (фотоны). В вакууме поле распространяется со скоростью света, полю присущи характерные для него электрические и магнитные свойства, доступные наблюдению.
Электромагнитное поле оказывает силовое воздействие на электрические заряды. Силовое воздействие положено в основу определения двух векторных величин, описывающих поле: напряженности электрического поля Е (В/м) и индукции магнитного поля В (Тл = В с/м2). На заряд q (Кл), движущийся со скоростью v~ в электрическом поле напряженности Е и магнитном поле индукции В, действует сила Лоренца F = q E + q[v В}.
Электромагнитное поле обладает энергией, массой и количеством движения, т.е. такими же атрибутами, что и вещество. Энергия в единице объема, занятого полем в вакууме, равна сумме энергий электриче-
- ч £о£2 '
скои и магнитной компонент поля и равна Жэм =—--------------- +------- , здесь
{ 2 2Ро
с0 =---------------- — электрическая постоянная, Ф / м; ц0 = 4л-10'7— маг-
4Я-9-10
нитная постоянная, Гн / м. Масса электромагнитного поля в единице объема равна частному от деления энергии поля Wэм на квадрат скорости распространения электромагнитной волны в вакууме, равной скорости света. Несмотря на малое значение массы поля по сравнению с массой вещества, наличие массы поля указывает на то, что процессы в поле являются процессами инерционными. Количество движения единицы объема электромагнитного поля определяется произведением массы единицы объема поля на скорость распространения электромагнитной волны в вакууме.
Электрическое и магнитное поля могут быть изменяющимися и неизменными во времени. Неизменным в макроскопическом смысле электрическим полем является электростатическое поле, созданное совокупностью зарядов, неподвижных в пространстве и неизменных во време
ни. В этом случае существует электрическое поле, а магнитное отсутствует. При протекании постоянных токов по проводящим телам внутри и вне их существуют электрическое и магнитное поля, не влияющие друг на друга, поэтому их можно рассматривать раздельно. В изменяющемся во времени поле электрическое и магнитное поля, как упоминалось, взаимосвязаны и обусловливают друг друга, поэтому их нельзя рассматривать раздельно.
§ 1.2. Интегральные и дифференциальные соотношения между основными величинами, характеризующими поле. Электромагнитные поля могут быть описаны интегральными или дифференциальными соотношениями. Интегральные соотношения относятся к объему (длине, площади) участка поля конечных размеров, а дифференциальные — к участку поля физически бесконечно малых размеров. Они выражают
 ся операциями градиента, дивергенции, ротора (раскрытие операции grad, div и rot в различных системах координат см. во втором томе книги). В макроскопической теории поля описывают свойства поля, усредненные по бесконечно малому физическому объему и во времени. Этот объем, в отличие от математически бесконечно малого объема, может содержать большое число атомов вещества. Дифференциальные уравнения макроскопической теории поля не описывают поля внутри атомов, для чего, как известно, служат уравнения квантовой теории поля.
ся операциями градиента, дивергенции, ротора (раскрытие операции grad, div и rot в различных системах координат см. во втором томе книги). В макроскопической теории поля описывают свойства поля, усредненные по бесконечно малому физическому объему и во времени. Этот объем, в отличие от математически бесконечно малого объема, может содержать большое число атомов вещества. Дифференциальные уравнения макроскопической теории поля не описывают поля внутри атомов, для чего, как известно, служат уравнения квантовой теории поля.
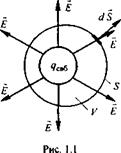
В электростатическом поле поток вектора напряженности электрического поля Е через
замкнутую поверхность (рис. 1.1) равен свободному заряду <?св6, находящемуся внутри этой поверхности, деленному на е0 ег (теорема Гаусса):
= (1.1)
где dS — элемент поверхности, направленный в сторону внешней нормали к объему; ег — относительная диэлектрическая проницаемость диэлектрика.
В дифференциальной форме теорему Гаусса записывают так:
= (L2)
(Рсвб — объемная плотность свободного заряда, Кд / м3).
Переход от (1.1) к (1.2) осуществляют делением обеих частей (1.1) на объем Г, находящийся внутри поверхности 5, и стремлением объема V к нулю. _
Физически div Е означает исток вектора в данной точке.
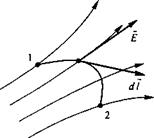 В электростатическом и стационарном электрическом полях на заряд q действует сила F = qE. Отсюда следует, что Е может быть определена как силовая характеристика поля Е = limF/g. Если q под действием сил поля переместится из точки 1 в точйу*0 2 (рис. 1.2), то силы поля совершат работу A = q\^Edl, где dl — элемент пути из 1 в 2.
В электростатическом и стационарном электрическом полях на заряд q действует сила F = qE. Отсюда следует, что Е может быть определена как силовая характеристика поля Е = limF/g. Если q под действием сил поля переместится из точки 1 в точйу*0 2 (рис. 1.2), то силы поля совершат работу A = q\^Edl, где dl — элемент пути из 1 в 2.
Под разностью потенциалов Ut2 между точками 1 и 2 понимают работу, совершаемую силами поля при переносе заряда <7=1 Кл из точки 7 в точку 2,
2
77]2=<p1-<p2=j£<7/; (1.3)
,, 1 Рис. 1.2
17|2 не зависит от того, по какому пути происходило перемещение из точки 1 в точ
ку 2. Выражению (1.3) соответствует дифференциальное соотношение
£ = -grad<p. (1.4)
Градиент <р (gradcp) в некоторой точке поля определяет скорость изменения <р в этой точке, взятую в направлении наибольшего его возрастания. Знак минус означает, что Е и gradcp направлены противоположно.
Электрическое поле называют потенциальным, если для него §Edl =0. Электрическое поле поляризованного диэлектрика описывается вектором электрического смещения (индукции)
D = e0£ + P, (1.5)
где Р — поляризованность диэлектрика, равная электрическому моменту единицы объема поляризованного диэлектрика.
В стационарном неизменном во времени электрическом поле в проводящей среде в смежные моменты времени распределение зарядов одинаково, поэтому для этого поля справедливо определение разности потенциалов по формуле
2
(7|2 = \Ed~l.
।
Внутри источника постоянной ЭДС результирующая напряженность электрического поля £рез равна векторной сумме потенциальной (ку- лоновой) составляющей £пот и сторонней составляющей £стор :
£ = £ + £ ■
рез *^пот ^стор’
£СТОр разделяет заряды внутри источника; она обусловлена химическими, электрохимическими, тепловыми и другими процессами неэлектро
статического происхождения и направлена встречно Ёпт. Внутри источника ЭДС при е(/), являющейся функцией времени, напряженность электрического поля имеет две составляющие: £стор и £пот, но £стор, разделяющая заряды внутри источника, обусловлена электромагнитными процессами, а не перечисленными выше. В электромагнитном поле могут протекать электрические токи. Под электрическом током понимают направленное (упорядоченное) движение электрических зарядов. Ток в некоторой точке поля характеризуется плотностью 8 (А/м?). Известны три вида тока: ток проводимости (плотностью 8пр), ток смещения (плотностью 8СМ) и ток переноса (плотностью 8пер). Ток проводимости протекает в проводящих телах под действием электрического поля, плотность его пропорциональна Е:
8пр = у£, (1.6)
где у — удельная проводимость проводящего тела, Ом-|-м-1. В металлах ток проводимости представляет собой упорядоченное движение свободных электронов, в жидкостях — движение ионов.
Плотность тока смещения в диэлектрике равна производной по времени от вектора электрического смещения D = е0Ё + Р.
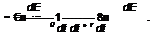 | |||||
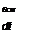 | |||||
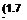 | |||||
dE ,
Слагаемое s0----------- составляющая тока смещения, обусловленная из
менением во времени напряженности поля £ в вакууме. Под вакуумом’' в курсе ТОЭ будем понимать не просто сверхразреженную среду, не пустоту, где ничего нет, а мировую материальную среду с особыми свой-
’’ Из чего состоят вакуум и электрические заряды, создающие в нем ток смещения, какие в вакууме и в самих зарядах происходят физические процессы и по каким законам — достоверно пока неизвестно.
Изучение процессов в вакууме в настоящее время проводится по нескольким направлениям. Наиболее известны два из них. Первое направление исследования (первая гипотеза) основывается на квантовой теории и на теории относительности [Физическая энциклопедия. Т. 5. 1998. С. 317; БСЭ. 3-е изд. Т. 27. С. 337]. Второе направление исследований [Ацюковский В.А. Общая эфиродинамика. М/. Энергоатомиздат. 1990] основывается на предположении о том, что процессы в микромире вакуума подчиняются всем известным в настоящее время законам макромира газовой динамики реального вязкого сжимаемого газа и что ограничение скорости различных физических процессов в физическом вакууме величиной скорости света З Ю8 м/с справедливо только для электромагнитных процессов и не справедливо для гравитационных.
Согласно первому направлению исследования под вакуумным состоянием понимают состояние поля, в котором оно вовсе не имеет частиц (квантов), когда его энергия, оставаясь огромной, минимальна. В этом состоянии электромагнитные и другие виды полей испытывают флюктуации, при которых в вакууме рождаются электронно-позитронные пары.
Эти пары ведут себя как связанные заряды и под действием электрического поля смещаются, подобно тому как смещаются связанные заряды в диэлектрике. Процесс смещения электронно-позитронных пар под действием электрического поля называют поляризацией вакуума.
ствами. В течение многих столетий эту среду называли эфиром, а в последние десятилетия ее стали именовать физическим вакуумом, самим названием подчеркивая, что она обладает физическими свойствами. Слагаемое dPIdt обусловлено изменением поляризованности во времени (изменением расположения связанных зарядов в диэлектрике при изменении Е во времени). В качестве примера тока смещения может быть назван ток через конденсатор. Ток переноса вызывается движением электрических зарядов в свободном пространстве. Примером тока переноса может служить ток в электронной лампе. Если положительный заряд объемной плотности р+ движется со скоростью v+ и отрицательный заряд объемной плотности р_ со скоростью v_, то плотность тока переноса в этом поле 5пер = р+ v+ + р_ v_ в явном виде не зависит от напряженности Е в данной точке поля. Если в некоторой точке поля одновременно существовали бы все три вида тока, то полная плотность тока $пол = $пР +5см +$пер- Для большинства задач ток переноса отсутствует.
Ток — это скаляр алгебраического характера. Полный ток через поверхность S’ равен
/пол=/8пол^. (1.8)
.S'
Если в электромагнитном поле выделить некоторый объем, то ток, вошедший в объем, будет равняться току, вышедшему из объема, т. е.
/8ПОЛ^5=0, (1.9)
где dS — элемент поверхности объема, он направлен в сторону внешней по отношению к объему нормали к поверхности. Последнее уравнение выражает принцип непрерывности полного тока: линии полного тока представляют замкнутые линии, не имеющие ни начала, ни конца. Элек-
Вторым основным процессом в вакууме является испускание фотона свободным электроном (позитроном) с последующим его поглощением другим или тем же электроном за очень короткое время Д/, равное, примерно, КГ21 с. За это время заряды перемещаются на расстояние Ах. Процесс называют виртуальны.», а сами заряды — виртуальными.
Для каждой пары виртуальных частиц выполняется закон сохранения заряда, но в рамках соотношения неопределенностей наблюдаются местные нарушения закона сохранения энергии и закона сохранения импульса. Эти нарушения состоят в том, что каждая виртуальная частица во время ее существования обладает разбросом энергии ЛИ' >ЫЛ1 и разбросом импульса Лт>И/Лх, где постоянная Планка h = 6,626-10"34 Дж-с.
Согласно второму направлению исследования вакуума, в нем образуются тороидальные вихри уплотненного эфира, обладающие огромной кольцевой и тороидальной скоростью. Эти вихри и являются электрическим зарядами. Тороидальная составляющая винтового движения создает магнитное поле, кольцевая — электрическое. Знак заряда зависит от того, является ли вихревое движение по отношению к кольцевому лево- или правовинтовым. Фотон — это двухрядная цепочка линейных (не кольцевых) вихрей, в которой вихри одного ряда вращаются в одну сторону, а другого ряда — в противоположную. Во втором направлении исследования установлено, что плотность физического вакуума численно равна величине электрической постоянной с0 = 8,86-10" 2 кг/м3 (Фарад/м в системе МКСА — эквивалент кг / м3 в системе МКС).
Носителями тока электрического смещения в физическом вакууме согласно первому направлению исследования вакуума являются электронно-позитронные пары, согласно второму — свободные электрические заряды (электроны и протоны).
трические токи неразрывно связаны с магнитным полем. Эта связь в неферромагнитной среде определяется интегральной формой закона полного тока
^Hdl = ^dl = Inon- (1.10)
' Mo
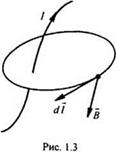 циркуляция вектора напряженности магнитного поля Н (А/м) по замкнутому контуру равна полному току /пол, охваченному этим контуром; dl — элемент длины контура (рис. 1.3). Таким образом, все виды токов, хотя и имеют различную физическую природу, обладают свойством создавать магнитное поле. В неферромагнитной среде магнитная индукция
циркуляция вектора напряженности магнитного поля Н (А/м) по замкнутому контуру равна полному току /пол, охваченному этим контуром; dl — элемент длины контура (рис. 1.3). Таким образом, все виды токов, хотя и имеют различную физическую природу, обладают свойством создавать магнитное поле. В неферромагнитной среде магнитная индукция
В = ^Н. (1.11)
Ферромагнитные вещества обладают спонтанной намагниченностью. Характеристикой ее является магнитный момент единицы объема вещества J (его называют намагниченностью). Для ферромагнитных веществ
В = р0(Н +J) = n0VrH = ца/7, (1.12)
где ца— относительная и абсолютная маг
нитная проницаемость, соответственно.
Напряженность магнитного поля в ферромагнитной среде
Н = — -J (1.13)
Но
равна разности двух векторных величин: В/ц0 и J.
Закон полного тока в интегральной форме для любой среды принято записывать в виде
Р?<"=Л,ол (1.14)
или в дифференциальной форме
rot Н = у £ + (1.15)
dt
|
Запись (1.15) закона полного тока получили из (1.14), поделив обе части его на площадь AS, охваченную контуром интегрирования, устремив AS к нулю и учтя плотность тока смещения dD ч
----- . Физически ротор (rot) характеризует d t . ...
поле в данной точке в отношении способности к образованию вихрей.
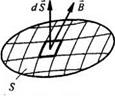
Плотность тока переноса в правой части последнего уравнения не учтена, так как он обычно отсутствует в задачах, решаемых с помощью этого уравнения. Магнитный поток через некоторую поверхность S
(рис. 1.4) определяют как поток вектора В через эту поверхность:
<b = \BdS. (1.16)
s
Поток Ф — это скаляр алгебраического характера, измеряется в веберах (Вб = В с). Если поверхность S замкнутая и охватывает объем К, то поток, вошедший в объем, равен потоку, вышедшему из него, т. е.
fBc/S = O. (1.17)
Это уравнение выражает принцип непрерывности магнитного потока. Линии магнитной индукции — это замкнутые линии.
В 1831 г. М. Фарадей сформулировал закон электромагнитной индукции: ЭДС еинд, наведенная в некотором одновитковом контуре изменяющимся во времени магнитным потоком, пронизывающим этот контур, определяется выражением
. - - (1Ф
еинд = ^madl = (1.18)
dt
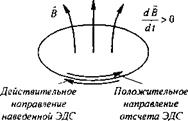 где Ёинд — индукционная составляющая напряженности электрического поля. Знак минус обусловлен правой системой отсчета: принято, что положительное направление отсчета для ЭДС и направление потока при его возрастании связаны правилом правого винта (рис. 1.5).
где Ёинд — индукционная составляющая напряженности электрического поля. Знак минус обусловлен правой системой отсчета: принято, что положительное направление отсчета для ЭДС и направление потока при его возрастании связаны правилом правого винта (рис. 1.5).
Если контур многовитковый (катушка с числом витков w), то
d'V
(119) dt
Здесь Т — потокосцепление катушки, равное сумме потоков, пронизывающих отдельные витки катушки,
Т =ф, +ф2 +... + Фи„ (1.20)
Если все витки w пронизываются одинаковыми потоками Ф, то
Т = и'Ф,
где Т— результирующее потокосцепление, оно может создаваться не только внешним по отношению к данному контуру потоком, но и собственным потоком, пронизывающим контур, при протекании по нему тока. В проводнике длиной dl, пересекающем магнитные силовые ли-
| нии неизменного во времени магнитного поля - индукции В (рис. 1.6), вследствие силы Лоренца наводится ЭДС |
| Рис. 1.6 |
| = B[d7 v], |
| (1.21) |
| где v — скорость перемещения проводника относительно магнитного поля. В (1.21) В скаляр- но умножается на векторное произведение dl и V. Если в результате расчета по (1.21) </еинд>0, то (/еинд направлена по dl. |
| В 1833 г. русский академик Э.Х. Ленц установил закон электромагнитной инерции. При всяком изменении магнитного потока, сцепляющегося с каким-либо проводящим контуром, в нем возникает индуктированная ЭДС, стремящаяся вызвать в контуре ток, который: 1) препятствует изменению потокосцепления контура; 2) вызывает механическую силу, препятствующую изменению линейных размеров контура или его повороту. Закон электромагнитной индукции, примененный к контуру бесконечно малых размеров, записывают так: |
| - дВ rot £ =--- dt |
| (1.22) |
| (в последней формуле индукционную составляющую напряженности поля £инд принято обозначать Е). Обобщая, можно сказать, что электромагнитное поле описывают четырьмя основными уравнениями в интегральной форме: |
| f// <// = /пол; еинд = f £инд jBdS = O, ^EdS = -^-. £0Er |
| (1.23) |
| Этим уравнениям отвечают четыре уравнения в дифференциальной форме: |
| rot Я = уЁ + ^-‘, dt |
| (1.24) |
| - дВ rot Е =-- ; dt |
| (1.25) |
| div В = 0; |
| (1.26) |
| div£ = -B«6 |
| (1.27) |
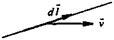
Они сформулированы в 1873 г. Дж. Максвеллом в его «Трактате об электричестве и магнетизме». Их называют уравнениями Максвелла или уравнениями макроскопической электродинамики.
Уравнение (1.24) означает, что вихревое магнитное поле создается токами проводимости и токами смещения. Уравнение (1.25) свидетельствует о том, что изменение магнитного поля во времени вызывает вихревое электрическое поле. Уравнение (1.26) — что магнитная индукция в неферромагнитной среде не имеет истоков и уравнение (1.27) — что истоком линий Ё являются свободные заряды. Частные производные в уравнениях (1.24) и (1.25) учитывают, что уравнения записаны для неподвижных тел и сред в выбранной системе координат.
Джеймс Максвелл обобщил и дополнил работы предшествующих ученых А. Ампера, М. Фарадея, Д. Генри, Э. Ленца, Г. Гельмгольца, ввел понятие об электрическом смещении в диэлектрике, о токе смещения в диэлектрике и создал систему уравнений (1.24)—(1.27), с помощью которых могут быть исследованы процессы в изменяющихся во времени электромагнитных полях и электрических цепях.
§ 1.3. Подразделение электротехнических задач на цепные и полевые. Задачи, с которыми приходится встречаться на практике, могут быть подразделены на две большие группы. Первая группа — цепные задачи. Они могут быть решены с помощью уравнений поля в интегральной форме. В этой группе используются понятия «ток», «магнитный поток», «электрическое» и «магнитное напряжение», «потенциал», «ЭДС», «МДС» (магнитодвижущая сила), «резистивное», «индуктивное» и «емкостное сопротивление». Для решения задач второй группы — полевых задач — применяют уравнения поля в дифференциальной и интегральной формах. Цепные задачи рассматривают в I томе учебника ТОЭ (курса теории цепей), задачи теории поля — во II томе учебника ТОЭ. Четкой границы между двумя группами задач нет, так как любая цепная задача с увеличением частоты перерастает в полевую (все более проявляются малые (паразитные) параметры и резко возрастает излучение энергии в окружающее пространство).
Основными уравнениями теории электрических цепей являются уравнения (законы) Кирхгофа. Первый закон Кирхгофа для электрических цепей следует из принципа непрерывности полного тока, а для магнитных цепей — из принципа непрерывности магнитного потока.
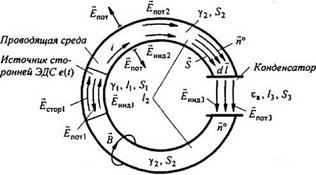
Покажем, что уравнение второго закона Кирхгофа для цепи переменного тока вытекает из основных уравнений электромагнитного поля. С этой целью обратимся к рис. 1.7. Цепь образована источником сторонней ЭДС е(/), являющейся функцией времени (область 1 с проводимостью у,), проводящей средой (область 2 с проводимостью у2) и конденсатором (область 3, электрическая проницаемость ва).
В источнике ЭДС за счет работы механической силы при вращении ротора электрического генератора возникает сторонняя ЭДС е(/). Она создает внутри источника стороннюю напряженность электрического поля £стор, непрерывно разделяющую электрические заряды внутри источни-
 |
|
ка, так что на одном зажиме источника в некоторый момент времени создается плюс заряд, а на другом зажиме в тот же момент времени такой же по величине минус заряд. Эти заряды создают в цепи потенциальное электрическое поле с напряженностью Епот и изменяющийся во времени электрический ток /. Одновременно с разделением зарядов и протеканием тока по цепи возникает изменяющееся во времени магнитное поле индукции В, охватывающее проводник и по закону электромагнитной индукции создающее в цепи и диэлектрике индукционную составляющую электрического поля Ёинд. Электрические заряды, перемещающиеся по проводнику, создают в диэлектрике, окружающем проводник, потенциальную составляющую напряженности электрического поля Епот =-gradq> (где ф— электрический потенциал), направленную перпендикулярно к поверхности проводника.
Будем исходить из непрерывности полного тока i через поперечные сечения трех областей. Полагаем, что излучение энергии в окружающее пространство отсутствует (частота относительно невелика). В первой области напряженность электрического поля Е} состоит из трех компонент (сторонней, потенциальной и индукционной):
= Ястор! + 4ОТ| + £ин41> во второй — Ё2 = Ёпот2 + Ёинд2, в третьей — Е3 - ^потз + ^индз! $1 >$2>$з — площади поперечного сечения областей; dl — элемент длины, совпадающий по направлению с dS', п°— единичный вектор, совпадающий с направлением dl и S.
Для первой области
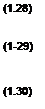 2 = у | ( ЕСТОр I + Епот; + ЕИНД i) ■$! ’ для второй
2 = у | ( ЕСТОр I + Епот; + ЕИНД i) ■$! ’ для второй
*' “ Y2 (^Пот2 ^имд2 > для третьей —
‘ = sa “гС^потЗ + ^индз)^3 ~ еаР(^потЗ + ^индз)^3> Р at
Умножим уравнения (1.28-1.30) на элемент длины пути dl = п° dl, учтем, что S = п° S, и перепишем их так:
| (^CTOpl ^ПОТ1 +£инд1)^ Q Yi | (1-31) |
| ^nm2+Em^dl = -!—dl- Y2S2 | (1-32) |
| (Enm3 + Ema3)dl = —l—dl. | (1-33) |
Реа S3
Проинтегрируем (1.31) по длине 1 -го участка, уравнение (1.32) по длине 2-го участка и уравнение (1.33) по длине 3-го и сложим их.
Получим
J ^стор| J^nOTl + J^710t2 + J^nOT-З ^1 "*■
/, />I, h ,
«(')
+ J £Инд1 + J £инд2 dl + J £инд3 dl =
/|'г I,.
. , dl , dl i r dl i f. , 1 , dl
= i I +[ + —I ; — = \idt, — = ] .
/,71^1 12Уг^2 Pl,ea^3 P C /, Ea$3
Окончательно,
i(Rx+R2) + ^ + ^\idt = e(t), (1.34)
где R\ и R2 — резистивные сопротивления участков / и 2; С — емкость конденсатора.
Второй закон Кирхгофа для магнитных цепей следует из закона полного тока.
Рассмотрим свойства элементов электрической цепи конденсатора и индуктивной катушки.
§ 1.4. Конденсатор. Между двумя любыми проводящими телами, разделенными диэлектриком, существует электрическая емкость. Для создания определенного значения емкости служат конденсаторы. На рис. 1.8 изображен плоский конденсатор, на рис. 1.9 — цилиндрический. Если заряд на одной обкладке (электроде) конденсатора + q, на другой - q, то
| dl |
Рис. 1.8
 | 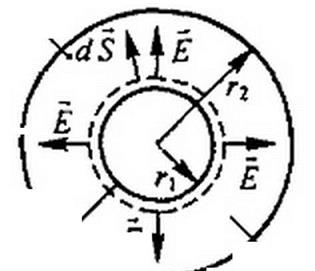 | ||
Рис. 1.9
в пространстве между обкладками существует электрическое поле и между обкладками имеется напряжение U. Заряд д пропорционален (7:
q=CU.
Коэффициент пропорциональности С называют емкостью
(135)
Емкость зависит от геометрических размеров конденсатора и от электрических свойств диэлектрика между обкладками. От напряжения U емкость, как правило, не зависит. Исключение составляют конденсаторы, у которых между обкладками находится сегнетодиэлектрик (у сегнетоди- электрика является функцией £). Единицей емкости является фарад (Ф) или более мелкие единицы микро-, нано- и пикофарад: 1 мкФ = = 10"6 Ф; I нФ = 10’9 Ф; 1 пФ = 10’12 Ф.
Пример 1. Вывести формулу для емкости плоского конденсатора (рис. 1.8. а). Площадь его каждой пластины (с одной стороны) 5. расстояние между пластинами а, относительная диэлектрическая проницаемость диэлектрика гг.
Решение. На рис. 1.8. 6 (вид сбоку) показаны силовые линии. В основной области поле однородно. На краях имеется некоторая неоднородность, которую здесь учитывать не будем. Е направлена от заряда + q к заряду - q. Напряжение между электродами U Edi = [* £ cos 0* dl - Е а. Охватим верхний электрод замкнутой поверхностью (ее след на рис. 1.8, б показан штриховой линией) и применим к ней теорему Гаусса:
$EdS = ES = -£
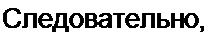 | |||||||||||
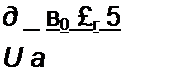 | |||||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||
внутреннем электроде радиусом Г] находится заряд + д, на наружном электроде радиусом г2 — заряд - д.
Решение. Окружим внутренний электрод цилиндрической замкнутой поверхностью радиуса г (r, <i'<r2). След этой поверхности показан штриховой линией на рис. 1.9, б. Поток вектора Е проходит через боковую поверхность, через торцы поток отсутствует, так как на торцах dS и Е взаимно перпендикулярны:
 |
$EdS = JfcosO’ dS-E2nrl- бок пов
£ = 2
2 Л Г I £0 £
Напряжение между электродами
(/ = [Edr =--------- =----------------- $—-kA.
’ 2 я £0 £г / ' г 2 я £0 er I Г)
Емкость *
с_д ЗлЕрВ, ~и~ кА ' и
В конденсаторе емкостью С, между электродами которого напряжение и, запасена электрическая энергия
 Си2 д2
Си2 д2
2 2С
При изменении заряда q во времени через конденсатор по диэлектрику течет ток смещения
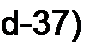 ;=^=сД
;=^=сД
dt dt
Положительное направление отсчета тока i совпадает с положительным направлением отчета напряжения и.
Из (1.37) следует, что
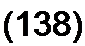 I г. , и- — \idt.
I г. , и- — \idt.
С J
§ 1.5, Индуктивность. Явление самоиндукции. Если по какой-либо катушке (контуру) будет протекать ток, то он создаст магнитное поле и катушка будет пронизываться магнитным потоком. Потокосцепление катушки ¥ будет пропорционально току /: = Коэффициент пропор
циональности L между Т и i называют индуктивностью:
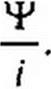
Индуктивность L (Гн) зависит от геометрических размеров катушки, числа ее витков и от магнитных свойств сердечника, на котором она намотана. Если ток z будет изменяться во времени, по закону электромагнитной индукции в катушке наведется ЭДС , которую называют ЭДС самоиндукции-.
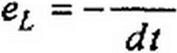 |
|
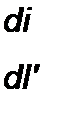 | |||
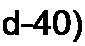 | |||
Положительные направления отсчета для / и eL совпадают (е{ пропорциональна скорости изменения тока /).
Если сердечник, на который намотана катушка, ферромагнитный, то 4х — нелинейная функция тока L В этом случае
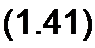 d4(i) = d4(i)di = di
d4(i) = d4(i)di = di
dt ~ di dl' -’иф dt
(£диф называют дифференциальной индуктивностью, она является нелинейной функцией тока /).
В магнитном поле уединенной катушки индуктивностью £, по которой течет ток /, запасается магнитная энергия
/ ' £ / 2
= [idY = fLidi =----------------------- .----------------------- (1.42)
О о
Из (1.42) следует, что
2W
Ь = (1.43)
I2
Пример 3. Вывести формулу для индуктивности /. двухпроводной линии передачи длиной /, расположенной в воздухе, при расстоянии между осями проводов d и радиусе провода г с d. Полагать / » d и нс учитывать магнитный поток поперечных сторон петли.
Решение. Двухпроводная линия (рис. 1.10.а, о) представляет собой как бы один большой виток. Пропустим по ней ток /. Напряженность поля в произвольной точке между проводами на расстоянии х от левого провода на линии, соединяющей оси проводов, по закону полного тока равна //(2пх), а результирующая напряженность поля равна сумме напряженностей от каждого из проводов:
| ||||||
| ||||||
| ||||||

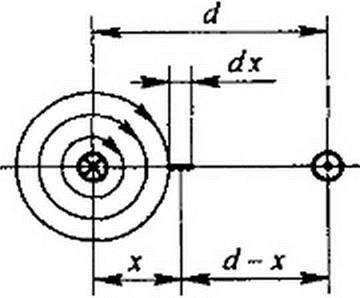
Поток через заштрихованную площадку dS=ldx равен
2п \х d-х J л г
При d э» г
д=±=мо11л£
/ я г
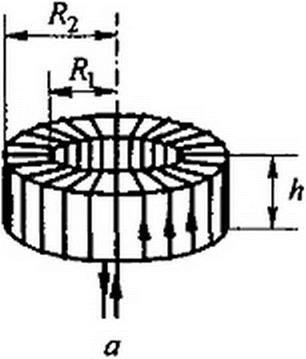
Пример 4. Определить индуктивность катушки (рис. 1.11, а) с числом витков н«] = 1000. равномерно намотанной на сердечник прямоугольного сечения, внутренний радиус которого Я) =4 см, наружный Я2 = 6 см, высота Л = 2 см, рг сердечника равна 80.
 | |||
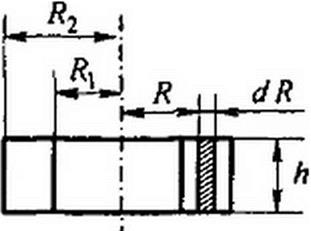 | |||
Рис. 1.11
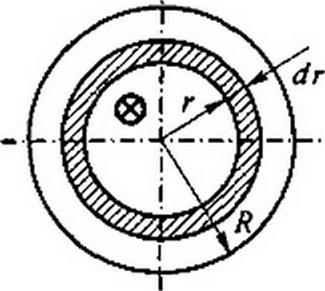
Решение. Пропустим по катушке ток / и определим напряженность поля в сердеч
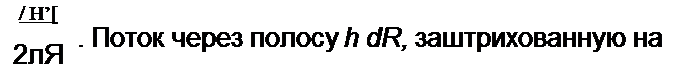 | ||||
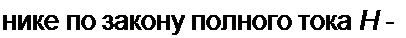 | ||||
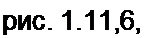 | ||||
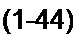
| ||||
| ||||
2пЯ
Потокосцепление
Т = if, ф = М| 1
«1
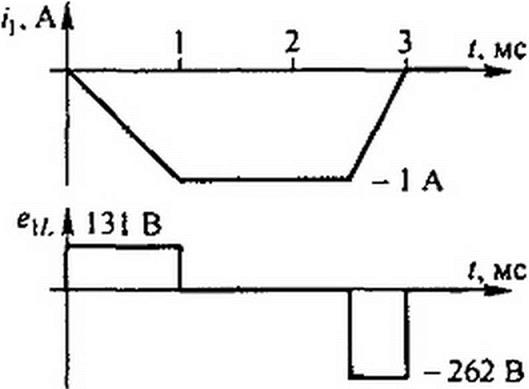
Подстановка числовых значений дает L = 4*//= 0,131 Гн.
Пример 5. Вывести формулу для индуктивности цилиндрического провода длиной / радиусом Я. обусловленной потокосцеплением в теле самого провода. На рис. 1.12 пока
зан вид провода с торца.
Решение. Пропустим вдоль провода постоянный ток /. По закону полного тока напряженность поля Н на расстоянии / 2
г от оси провода равна току ------------- пг , охваченному окруж-
л Я2
ностью радиусом г и деленному на длину этой окружности 2 л г:
1г
2 тг R2
Индукция
Магнитная энергия, запасенная в теле провода,
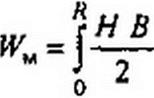 | |||
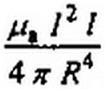 | |||
|
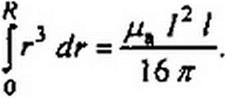 |
Воспользовавшись (i .43), получим:
/2 8л
§ 1.6 Взаимная индуктивность. Явление взаимоиндукции. На рис 1.13, а изображены два контура. По первому течет ток по второму — /2’ Поток Фи создаваемый первым контуром, частично замыкается, пронизывая только первый контур Фп, минуя второй, частично пронизывая и второй контур Ф12. Чтобы рисунок был более понятным, на нем изображено только по одной силовой линии каждого потока
Ф| —Ф]1
Аналогично поток, создаваемый вторым контуром:
Ф? = *$22 +<$2I-
Если первый контур имеет витков, то потокосцепление первого контура
W| (Ф । ± Ф ■> ।) = и’] Ф । ± W| Ф -> । — ЧИ । ± Ч/2 ] •
Потокосцепление второго контура (число витков м>2)
w 2 ($*2 И>2 Ф2 ± W2 Ф|2 = т2 ± ЧИ|2.
Знаки «+» соответствуют согласному направлению потока от своего тока и потока, создаваемого током в соседнем контуре. Знаки «-» соответствуют несогласному (встречному) направлению потоков (для этого
 |
|
 |
|
 |
|
Рис. 1.13
один из токов должен изменить направление). Потокосцепление пропорционально току /2, а ЧИ12 —току /|
*21 - VVj Ф2| - М i2-> *12 — ^2 Ф]2 “ М /(








