Урок №28 от 18. 05. 2020
по теме «Обыкновенные и десятичные дроби» (Подготовка к контрольной работе)
- Внимательно ознакомьтесь и оформите в тетради (перепишите или распечатайте и вложите) решение следующих заданий по теме «Обыкновенные и десятичные дроби».
Задания:
1) Трава при сушке теряет 80% своей массы.
а) Сколько тонн сушеной травы получится из 125 т свежей?;
б) Сколько тонн травы надо накосить, чтобы насушить 12 т сена?
2) Приблизить с недостатком и с избытком с точностью до 3 значащей цифры число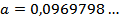 
3) Приблизить с округлением с точностью до сотых и найти разность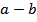 
чисел
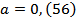и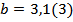 
.
4) Найдите длину отрезка, ограниченного точкам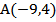и 
и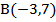 
координатной оси
Решение:
1) Трава при сушке теряет 80% своей массы.
а) Сколько тонн сушеной травы получится из 125 т свежей?;
б) Сколько тонн травы надо накосить, чтобы насушить 12 т сена?
Решение: а) Свежая трава – это вся трава, которая имеет, поэтому это 100%.
Свежая трава теряет 80%, то, что остается и есть сушеная, найдем сколько процентов травы остается после сушки, то есть выполним первое действие:
1) 
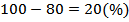– травы остаётся после сушки.
Найдём 20% от 125 т, то есть выполним второе действие:
2) 
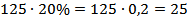(т).
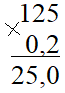
Ответ: 25 тонн сушеной травы получится из 125 т свежей.
б) Свежая трава – это вся трава, которая имеет, поэтому это 100%.
Свежая трава теряет 80%, то, что остается и есть сушеная, найдем сколько процентов травы остается после сушки, то есть выполним первое действие:
1) 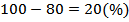– травы остаётся после сушки.
Найдем число 20%, которого составляет 12 т сена:
2) 
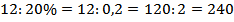(т).
Ответ: 240 тонн травы надо накосить, чтобы насушить 12 т сена.
2) Приблизить с недостатком и с избытком с точностью до 3 значащей цифры число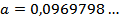
Решение: первая значащая цифра – это первая с лева направо отличная от нуля цифра в числе, таким образом, третья значащая цифра – это третья с лева направо отличная от нуля цифра в числе, то есть, цифра 9:
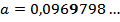
приблизить с недостатком, это значит, сделать число меньше исходного, отбросив лишние цифры в нём:
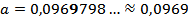с недостатком;
приблизить с избытком, это значит, сделать число больше исходного, отбросив лишние цифры в нём:
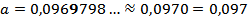с избытком.
Ответ: 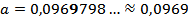с недостатком; 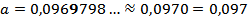с избытком.
3) Приблизить с округлением с точностью до сотых и найти разность 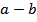чисел
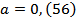и .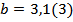
Решение: приблизим с округлением каждое из чисел:
приблизить с округлением, это значит, сделать число либо меньше исходного, если следующая за указанной цифра менее 5; либо сделать число больше исходного, если следующая за указанной цифра больше или равна 5, отбросив лишние цифры в нём:
;
;
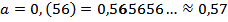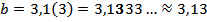найдём разность полученных чисел:
.
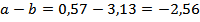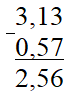
Ответ: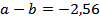 
.
4) Найдите длину отрезка, ограниченного точкам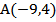и и 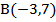координатной оси
Решение: Чтобы найти длину отрезка, ограниченного точками, координаты которых известны, нужно от большей координаты отнять меньшую, то есть:
.
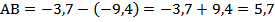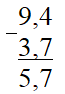
ЗАМЕЧАНИЕ: важно помнить, что длина – величина положительная!
Ответ: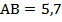 
.
- Выполните домашнее задание.
Домашнее задание:
1) Выполнить задания с карточки
Карточка
1) Трава при сушке теряет 70% своей массы.
а) Сколько тонн сушеной травы получится из 130 т свежей?;
б) Сколько тонн травы надо накосить, чтобы насушить 9 т сена?
2) Приблизить с недостатком и с избытком с точностью до 4 значащей цифры число
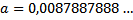
3) Приблизить с округлением с точностью до сотых и найти разность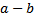 
чисел
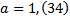и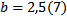 
.
4) Найдите длину отрезка, ограниченного точкам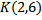и 
и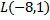 
координатной оси
- Решение домашнего задания оформите в тетради.
- Сфотографируйте в разборчивом виде.
- Передайте мне до 19.05.2020 через эл.дненик, Whatsapp, или VK.
Критерии оценивания карточки из домашнего задания:
Задание №1
1) Верное развернутое решение (со всеми пояснениями и способами решения) каждой задачи – 1 балл;
2) Развернутое решение (со всеми пояснениями и способами решения) каждой задачи, но с допущением одной вычислительной ошибки или верное развернутое решение (со всеми пояснениями и способами решения) каждой задачи, но с пропуском одного этапа решения или одного пояснения – 0,5 балла;
3) В любом случае не предусмотренном в пунктах 1 и 2 – 0 баллов.
Максимальное количество баллов за 1 задание – 2 балла.
Задание №2
1) Веное решение задания – 1 балл;
2) Решение с одной ошибком – 0,5 балла.
3) В любом случае не предусмотренном в пунктах 1 и 2 – 0 баллов.
Максимальное количество баллов за 2 задание – 1 балл.
Задание №3
1) Веное решение задания – 1 балл;
2) Решение с одной ошибком – 0,5 балла.
3) В любом случае не предусмотренном в пунктах 1 и 2 – 0 баллов.
Максимальное количество баллов за 3 задание – 1 балл.
Задание №4
1) Веное решение задания – 1 балл;
2) Решение с одной ошибком – 0,5 балла.
3) В любом случае не предусмотренном в пунктах 1 и 2 – 0 баллов.
Максимальное количество баллов за 4 задание – 1 балл.
Баллы суммируются. Максимальное количество баллов за всю работу – 5 баллов.
Перевод суммы баллов за все примеры в оценку:
ü 5 баллов – оценка «5»
ü 4 – 4,5 балла – оценка «4»
ü 2,5 – 3,5 балла – оценка «3»
ü менее 2,5 баллов – оценка «2»