1.9. Полные погрешности абсолютные
Домашняя работа 1
Вариант 4
| Вариант 4 | |
| P0Т, Вт | P0Э, Вт |
| 450 | 420 ±50 |
| Надежность результатов измерений α % | |
| 95 | |
| I, мА | R, Ом |
| 150 | 20 |
| 150 | 22.5 |
| 155 | 19.5 |
| 155 | 17 |
| 155 | 17.5 |
| 140 | 18 |
| 130 | 19 |
| 165 | 20 |
| 105 | 19 |
| 135 | 19.5 |
| Амперметра | Омметра |
| Класс точности | |
| 2.5 | 1 |
| Предел шкалы | |
| 200, мА | 100, Ом |
1. Даны отсчеты значений постоянного тока I и активного сопротивления R, через которое протекает этот ток, cнятые со шкал приборов известного класса точности. Получить результаты прямых измерений тока и сопротивления. Обеспечить надежность результатов измерений α.
2. С помощью косвенных измерений найти значение мощности, рассеянной на сопротивлении и оценить его погрешность.
3. Задано предполагаемое теоретическое значение мощности P0Т. Сделать вывод о согласии результатов измерений мощности и еетеоретического значения.
4. Ранее получено экспериментальное значение мощности P0Э. Сделать вывод о согласии результатов данных косвенных измерений мощности и её предыдущего экспериментального значения.
Решение:
1. Задание 1.
1.1. Инструментальные погрешности.
ΔаI = (КI∙АI)/100 = (2.5∙200∙10-3)/100 = 5mА
ΔаR = (КR ∙АR)/100 = (100∙1)/100 = 1 Oм
1.2. Определяем коэффициент даверия.
При α = 95% и N=10 tα,N = 2,3 При α = 95% и N=9 tα,N = 2,3.(Приложение 1).
1.3. Средние значения.
<I> = 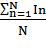 = 144 mА <R> =
= 144 mА <R> = 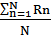 = 19.2 Om
= 19.2 Om
1.4. Средние квадратические отклонения отсчетов.
SI = 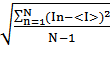 = 17.3 mА
= 17.3 mА
SR = 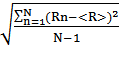 = 1.5 Om
= 1.5 Om
1.5. Проверяем отсчеты на наличие промахов. Аномальными отсчетами являются отсчет I9 = 105 mA и R2 = 22.5 Om. Вычисляем нормированное отклонениеI9 и R2 от среднего значения
ZI = 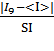 =
= 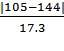 = 2.25 ZR =
= 2.25 ZR = 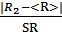 =
= 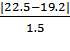 = 2.2
= 2.2
Согласно данным таблицы (Приложение 3) с критериями Шовене, количество опытов у ZI , при котором полученный отсчет нельзя считать промахом, равно 20. Это число больше, чем N=10 . Следовательно, отсчет, в котором значение тока получилось равным 105 mА является промахом и его нужно удалять из обрабатываемого ряда. Количество опытов у ZR, равно 18, больше, чем N=10. Следовательно, отсчет, в котором значение сопротивления получилось равным 22.5 Om, является промахом и его нужно удалять из обрабатываемого ряда.
1.6. Новое среднее значение.
<I> = 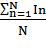 = 148.3 mА <R> =
= 148.3 mА <R> = 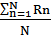 = 18.83 Om
= 18.83 Om
1.7. Среднее квадратическое отклонение.
SI = 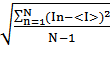 = 11.2 mА
= 11.2 mА
SR = 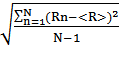 = 1.1 Om
= 1.1 Om
1.8. Случайные составляющие погрешности.
S<I> = 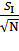 =
= 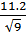 = 3.73 mA S<R> =
= 3.73 mA S<R> = 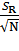 =
= 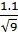 = 0.37 Om
= 0.37 Om
ΔслI = tα; N  S<I> = 2.3
S<I> = 2.3  3.73= 8.579 mA
3.73= 8.579 mA
ΔслR = tα; N  S<R> = 2.3
S<R> = 2.3  0.37= 0.851 Om
0.37= 0.851 Om
1.9. Полные погрешности абсолютные
ΔI = 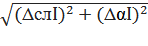 =
= 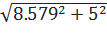 = 9.9
= 9.9
ΔR = 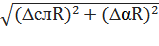 =
= 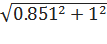 = 1.31
= 1.31
1.10. Полные погрешности относительные
δI = 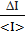 =
= 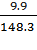 = 0.067 = 6.7%
= 0.067 = 6.7%
δR = 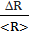 =
= 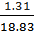 = 0.069 = 6.9%
= 0.069 = 6.9%
После округлений результат измерения тока записываем в виде:
I = (148.3 ± 9.9) mА
δ = 6.7%
α = 95 %
R = (18.83 ± 1.31) Om
δ = 6.9%
α = 95 %
2. Задание 2.
<I> = 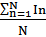 = 148.3 mА
= 148.3 mА
<R> = 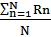 = 18.83 Om
= 18.83 Om
2.1. Среднее значение мощности.
<P>= <I>2 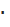 <R> = 414.13 mВт
<R> = 414.13 mВт
2.2. Относительные погрешности аргументов.
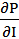 = 2I
= 2I 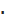 R = 5.58 В
R = 5.58 В 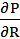 = I2 = 21.9 mА2
= I2 = 21.9 mА2
ΔPI= | 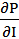 |
| 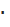 ΔI = 5.58
ΔI = 5.58 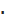 9.9
9.9 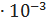 = 55.24 mВт
= 55.24 mВт
ΔPR = | 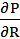 |
| 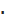 ΔR = 21.9
ΔR = 21.9 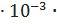 1.31= 28.7 mВт
1.31= 28.7 mВт
2.3. Полную погрешность абсолютную.
ΔP = 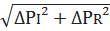 =
= 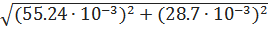 = 62.3 mВт
= 62.3 mВт
2.4. Полную погрешность относительную.
δP = 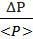 =
= 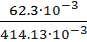 = 15 %
= 15 %
После округлений результат измерения тока записываем в виде:
P = (414.13 ± 62.3) mВт
δ = 15%
α = 95 %
3. задание №3
Предполагаемое теоретическое значение мощности P0Т, равное 450 mВт попадает в доверительный интервал полученного результата, значение которого лежит от 351.8 mВт до 476.43 mВт.
4. Экспериментальное значение мощности P0Э, равное (420 ±50) mВт сходится со значением результатов данных косвенных измерений мощности, равным (414.13 ± 62.3) mВт.
Домашняя работа 2
Вариант 1
1. Даны результаты прямых измерений некоторых физических величин и уравнение их связи с другой физической величиной.
2. Найти значение этой величины и оценить его погрешность. Погрешность косвенных измерений определить двумя способами:
1) с помощью вычисления частных производных измеряемой величины по ее аргументам;
2) с помощью вычисления конечных приращений.
Решение:
Вычисляем среднее значение.
< 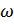 > =
> = 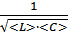 =
= 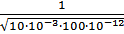 = 1
= 1 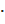 106 рад/с
106 рад/с
Вычисляем составляющие погрешности от каждого аргумента
△L 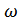 =
= 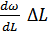 =
= 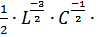 △L = 50000 рад/с
△L = 50000 рад/с
△C 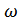 =
= 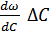 = =
= = 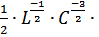 △С = 100000 рад/с
△С = 100000 рад/с
Вычисляем полную погрешность абсолютную.
△ 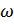 =
= 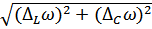 =
= 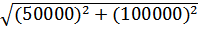 = 111803,4 = 0.1118034
= 111803,4 = 0.1118034
Вычисляем полную погрешность относительную.
δ 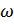 =
= 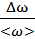 =
= 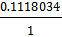 = 0.112 = 11.2%
= 0.112 = 11.2%
После округления записываем результат косвенных измерений:
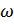 = (1±0.118) 106 рад/с
= (1±0.118) 106 рад/с
δ 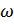 =11.2 %
=11.2 %
Алгоритм, использующий вычисление приращений измеряемой величины
по её аргументам.
Вычисляем приращения функции по её аргументам.
Δ 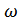 L= |
L= | 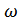 (L+ΔL, C) –
(L+ΔL, C) – 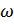 (L, C)|
(L, C)| 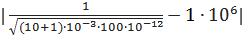 = 46537.4 рад/с
= 46537.4 рад/с
Δ 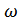 C= |
C= | 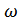 (L, C+ΔC) –
(L, C+ΔC) – 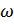 (L, C)| =
(L, C)| = 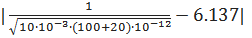 = 87129.1 рад/с
= 87129.1 рад/с
Вычисляем полную погрешность абсолютную
Δ 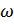 =
= 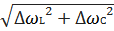 =
= 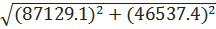 = 98778.6 рад/с
= 98778.6 рад/с
относительную:
δ 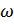 =
= 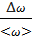 =
= 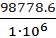 = 0.098= 9.8%
= 0.098= 9.8%
После округления записываем результат косвенных измерений:
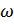 = (1±0.0988)
= (1±0.0988) 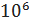 рад/с
рад/с
δ 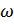 = 9.8 %
= 9.8 %
Алгоритм, использующий сложение абсолютных величин погрешностей
Вычисляем относительные погрешности аргументов
δL = 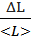 =
= 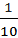 = 10%
= 10%
δC = 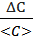 =
= 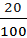 = 20 %
= 20 %
Вычисляем относительную погрешность функции по формулам приложения 2:
δ 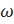 =
= 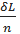 +
+ 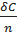 = 15%
= 15%
Вычисляем абсолютную погрешность функции
Δ 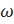 = <
= < 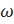 >δ
>δ 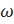 = 1
= 1 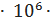 0.15 = 0.15
0.15 = 0.15 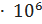 рад/с
рад/с
После округления записываем результат косвенных измерений:
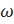 = (1±0.15)
= (1±0.15) 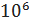 рад/с
рад/с
δ 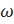 = 15%
= 15%








