Под вхождением переменной понимается место, которое переменная занимает в формуле. Элементарным произведением называется конъюнкт, в который любая переменная входит не более одного раза.

Дата: 2025-06-02; Просмотры: 12

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Формула φ ( x ₁ ,…, x_n ) называется импликантой формулы ψ ( x ₁ ,…, x_n ), если φ – элементарное произведение и 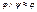, т.е для соответствующих формулам φ и ψ функций f_φ и f_ψ справедливо неравенство f_φ ≤ f_ψ. Формула φ ( x ₁ ,…, x_n ) называется импликантой функции f, если φ – импликанта СДНФ, представляющей f . Импликанта 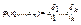формулы ψ называется простой, если после отбрасывания любой литеры из φ не получается формула, являющаяся импликантой формулы ψ.

Дизъюнкция всех простых импликант данной формулы называется СокращеннойДНФ .

Любая булева функция, не являющаяся константой 0, представима в виде СкДНФ. СкДНФ может содержать лишние импликанты, удаление которых не меняет таблицы истинности. Если из СкДНФ удалить все лишние импликанты, то получается Тупиковая ДНФ. Выбор из всех тупиковых форм формы с наименьшим числом вхождений переменных дает МинимальнуюДНФ.

Рассмотрим метод Квайна для нахождения МДНФ. Определим три операции:

1) операция полного склеивания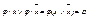

2) операция неполного склеивания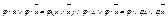

3) операция элементарного поглощения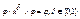

Теорема Квайна: Если исходя из СДНФ функции произвести все возможные операции неполного склеивания, а затем элементарного поглощения, то получится СкДНФ, т.е дизъюнкция всех простых импликант.

Для получения МДНФ из СкДНФ используется матрица Квайна, которая строится следующим образом: в заголовках столбцов таблицы записываются конституенты единицы СДНФ, а в заголовках строк – простые импликанты из СкДНФ. В таблице звездочками отмечаются те пересечения строк и столбцов, для которых конъюнкт, стоящий в заголовке строки, входит в конституенту единицы, являющейся заголовком столбца. В ТДНФ выбирается минимальное число простых импликант, дизъюнкция которых сохраняет все конституенты единицы, т.е каждый столбей матрицы Квайна содержит звездочку, стоящую на пересечении со строкой, соответствующей одной из выбранных импликант. В качестве МНДФ берется ТДНФ, имеющая наименьшее число вхождений переменных.

В силу принципа двойственности для булевых алгебр все приведенные понятия и рассуждения можно преобразовать для нахождения МКНФ.

45. Карты Карно. Построение МДНФ с помощью карт Карно.

Карта Карно для n переменных содержит 2 ⁿ ячеек, каждая из которых соответствует одной из возможных 2 ⁿ комбинаций значений n логических переменных x ₁ ,…, x_n. Карта строится в виде матрицы размера 2 ^{n - k} на 2 ^k так, что ее столбцы соответствуют значениям переменных x ₁ ,…, x_k, строки – значениям переменных x_{k +1} ,.., x_n, а соседние ячейки отличаются только значением одной переменной.

У каждой вершины n -куба есть ровно n смежных с ней вершин, т.е. вершин, отличающихся от нее только одной координатой. Поскольку в карте Карно каждая ячейка может иметь не более 4 ячеек, соседних по строке или столбцу, для представления точек, отличающихся только на одну координату, необходимо использовать и более удаленные ячейки.

Булева функция может быть представлена на карте Карно выделением 1-ячеек. Подразумевается, что необозначенные ячейки соответствуют 0-точкам.

Для построения импликант берутся всевозможные наборы 1-ячеек, образующих вершины некоторого k-куба (т.е. 2^k точек таких, что пары соседних отличаются ровно одной координатой). Совпадающие координаты образуют набор (δ₁,…,δ _{n - k} ) и требуемая импликанта имеет вид 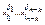, где x_j – переменная, соответствующая значению δ_j.

При наглядном размещении простых импликант в карте Карно удается непосредственно находить МДНФ, выбирая те простые импликанты, которые покрывают все единицы и имеют наименьшее возможное число вхождений переменных

46. Принцип двойственности. Самодвойственные функции.

Функция f ⁺ ( x ₁ ,…, x_n ) называется двойственной по отношению к функции f ( x ₁ ,…, x_n ), если 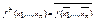. Двойственная функция получается из исходной при замене значений всех переменных, а также значений функции на противоположные.

Принцип двойственности: Если 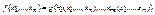, то 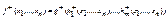. Таким образом, функция, двойственная суперпозиции функций, есть соответствующая суперпозиция двойственных функций.

Функция f(x₁,…,x_n) называется самодвойственной, если f ⁺ ( x ₁ ,…, x_n )= f ( x ₁ ,…, x_n ).

47. Теорема Жегалкина. Способы построения полиномов Жегалкина. Линейные функции.

Теорема Жегалкина: Всякая булева функция f ( x ₁ ,…, x_n ) представима полиномом Жегалкина, т.е в виде 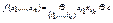, где в каждом наборе вида ( i ₁ ,…, i_k ) все i_j различны, а суммирование ведется по некоторому множеству таких несовпадающих наборов. Представление функции в виде полинома Жегалкина единственно с точностью до порядка слагаемых.

Полином Жегалкина называется нелинейным (линейным) если он (не) содержит произведения переменных. Линейность булевой функции равносильна линейности соответствующего полинома Жегалкина.

Аксиомы булева кольца и равенства, выражающие операции дизъюнкции, конъюнкции и отрицания через операции этого кольца:

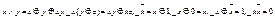. Если в эквивалентности 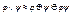формулы φ и ψ являются различными конституентами 1, то их произведение равно 0.

48. Классы Поста. Полные системы булевых функций. Теорема Поста. Базисы.

Система булевых функций F={f₁,…,f_n} называется полной, если любая булева функция представима в виде терма сигнатуры (f₁,…,f_n}, т.е в виде суперпозиции функций из F.

Классы Поста:

1) P₀={f|f(0,…,0)=0} - класс булевых функций, сохраняющих ноль

2) P₁={f|f(1,…,1)=1} – класс булевых функций, сохраняющих 1

3) S={f|f⁺=f} – класс самодвойственных функций

4) M – класс монотонных функций. Булева функция f(x₁,…,x_n) называется монотонной, если для любых наборов нулей и единиц (α₁,…,α_n) и (β₁,…,β_n) из условий α_i≤β_i следует f(α₁,…,α_n)≤f(β₁,…,β_n)

5) Класс I – это класс линейных функций. Булева функций f(x₁,…,x_n) называется линейной, если в булевом кольце 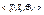функция f представима в виде .

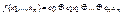Каждый класс Поста замкнут относительно операций замены переменных и суперпозиции.

Теорема Поста: Система F булевых функций тогда и только тогда является полной, когда для каждого из классов P₀, P₁, S, M, L в системе F найдется функция, не принадлежащая этому классу..

Теорема: Каждый базис содержит не более четырех булевых функций

Доказательство: Предположим, что существует базис F, состоящий более чем из четырех функций. По теореме Поста тогда получаем, что F состоит ровно из пяти функций, каждая из которых не принадлежит ровно одному классу Поста. Пусть f – функция из F, не принадлежащая классу P₀. Тогда f(0,…,0)=1 и f(1,…,1)=1, но тогда f не принадлежит классу самодвойственных функций, а это противоречит предположения.

49. Логические сети. Реализация булевых функций контактными схемами и схемами из функциональных элементов.

Мультиграф G =< M , U , R >, в котором выделено k вершин (полюсов), называется k -полюсной сетью. Сеть G, задаваемая неориентированным мультиграфом с k полюсами, в которой каждое ребро помечено буквой из алфавита 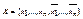, называется k -полюсной контактной схемой.

( k +1)-полюсная схема, в которой один полюс выделен (входной), а остальные полюса (выходные) равноправны, называется (1, k )-полюсником.

Ребра контактной схемы называются контактами. Контакт, соответствующий логической переменной x_i, называется замыкающим, он пропускает ток при x_i =1. Контакт, соответствующий литере 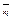, называется размыкающим, ток через него проходит при x_i =0. Функции 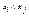соответствует последовательное соединение контактов, а функции 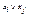- параллельное.

Пусть a , b – полюса контактной схемы Σ, [ a , b ] – некоторая цепь из a в b, K _{[ a , b ]} – конъюнкция литер, приписанных ребрам цепи [ a , b ]. Функция f_{a , b} ( X ), определяемая формулой 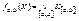, в которой дизъюнкция берется по всем простым цепям схемы, соединяющим полюса a и b, называется функцией проводимости между полюсами a и b схемы Σ. Говорят, что функция g ( X ) реализуется (1, k )-полюсником, если существует такой выходной полюс b_i , что f_{a , bi} ( X )= g ( X ), где a – входной полюс. (1,1)-полюсники называются смежными, если они реализуют одну и ту же булеву функцию. Сложностью (1,1)-полюсника называется число контактов. (1,1)-полюсник, имеющий наименьшую сложность среди эквивалентных ему схем, называется минимальным. Сложность минимального (1,1)-полюсника, реализующего функцию f, называется сложностью функции f в классе (1,1)-полюсников и обозначается L_π ( f ).

Ориентированная бесконтурная сеть, в которой полюса делятся на входные и выходные, называется схемой из функциональных элементов. Входные полюса помечаются символами переменных, а каждая вершина, отличная от входного полюса, некоторым функциональным символом. При этом должны выполняться следующие условия:

- если a – входной полюс, то полустепень захода вершины равна нулю: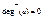

- если вершина a не является полюсом и помечена n-местным функциональным символом f, то 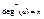и дуги, входящие в a пронумерованы от 1 до n.

Функциональным элементов называется всякий подмультиграф схемы, состоящий из невходного полюса a, помеченного соответствующим символом f, и вершины, из которых исходят дуги в вершину a.

Говорят, что функция f реализуется схемой Σ, если существует такой выход a из схемы Σ, что функция f_a, соответствующая терму выхода a, эквивалентна функции f.

Схемы из функциональных элементов с одним выходом, у которых входные полюса помечены символами x ₁ ,…, x_n, а вершины, отличные от входных, - символами 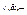, называются Xⁿ -функциональными схемами. Сложностью схемы из функциональных элементов называется число ее невходных вершин. Xⁿ-функциональная схема Σ, реализующая функцию f, называется минимальной, если всякая другая Xⁿ-функциональная схема, реализующая f, имеет сложность не меньшую, чем сложность схемы Σ. Сложность минимальной схемы, реализующей функцию f, называется сложностью функции f в классе схем из функциональных элементов и обозначается L ( f ).