Если х – логическая переменная, , то выражение: называется литерой. Литеры x и называются контрарными.
Элементарной конъюнкцией или конъюнктом называется конъюнкция литер. Элементарной дизъюнкцией или дизъюнктом называется дизъюнкция литер.
ДНФ – дизъюнкция конъюнктов. КНФ – конъюнкция дизъюнктов. Любая формула эквивалентна некоторой ДНФ и КНФ.
Алгоритм приведения формулы к ДНФ:
1) Выразить все логические операции, участвующие в построении формулы через дизъюнкции, конъюнкции и отрицания: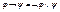 
, 
.
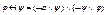2) Используя законы де Моргана, переносим все отрицания к переменным и сокращаем двойные отрицания.
3) Используя закон дистрибутивности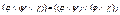 
, преобразуем формулу так, чтобы все конъюнкции выполнялись раньше дизъюнкций.
Алгоритм приведения формулы к КНФ:
4) Выразить все логические операции, участвующие в построении формулы через дизъюнкции, конъюнкции и отрицания: , .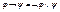
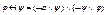5) Используя законы де Моргана, переносим все отрицания к переменным и сокращаем двойные отрицания.
6) Используя закон дистрибутивности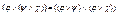 
, преобразуем формулу так, чтобы все дизъюнкции выполнялись раньше конъюнкций.
43. Теорема Шеннона. Теорема о функциональной полноте. Способы построения СДНФ и СКНФ.
Пусть ( x 1 ,…, xn ) – набор логических переменных, ∆= (δ1,…,δ n ) – набор нулей и единиц. Конституентой единицы набора ∆ называется конъюнкт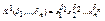 
. Конституентой нуля набора ∆ называется дизъюнкт 
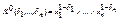. СДНФ – дизъюнкция некоторых конституент единицы, среди которых нет одинаковых. СКНФ – конъюнкция некоторых коституент нуля, среди которых нет одинаковых. Рассмотрим разложение булевой функции f ( x 1 ,…, xn ) по k переменным.
Первая теорема Шеннона: Любая булева функция f ( x 1 ,…, xn ) представима в виде разложения Шеннона: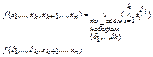 
Доказательство: Заметим, что 
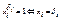. Подставим произвольно вместо первых k переменных их значения: 
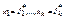. Тогда левая часть доказываемой формулы равна 
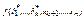. Правая часть представляет собой дизъюнкцию 2k конъюнкций вида 
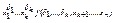, которые этой подстановкой разбиваются на два класса. К первому классу относится конъюнкция, у которой набор (δ1,…,δk) совпадает с набором 
: 
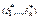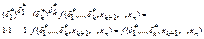. Эта конъюнкция равна Евой части формулы. Ко второму классу относится 2k-1 конъюнкций, у каждой из которых хотя бы в одной переменной xi, 
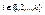выполнимо условие 
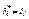. Следовательно каждая из них равна нулю. Используя закон 
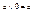, получаем, что левая и правая части формул равны при любой подстановке переменных x1,…,xn.
Вторая теорема Шеннона: Любая булева функция f ( x 1 ,…, xn ) представима в виде разложения Шеннона: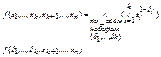 
.При k = n, для булевой функции f ( x 1 ,…, xn )≠0 получаем ее представление в виде СДНФ: 
.
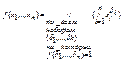Для булевой функции f ( x 1 ,…, xn )≠1, получаем представление в виде СДНФ: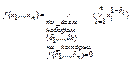 
.
Теорема о функциональной полноте: Для любой булевой функции f найдется формула φ, представляющая функцию f. Если f ≠0, то φ однозначно представима в виде СДНФ: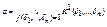 
. Если f ≠1, то φ однозначно представима в виде СКНФ: 
.
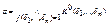Приведение ДНФ к СДНФ:
1) Данную формулу приводим к ДНФ
2) Если в конъюнкт входит некоторая переменная вместе со своим отрицанием, то этот конъюнкт удаляется из ДНФ
3) Если в конъюнкт одна и та же литера xδ входит несколько раз, то мы удаляем их все кроме одной
4) Если в некоторый конъюнкт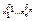 
не входит переменная y, то заменяем его на эквивалентную формулу 
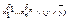и применяем закон дистрибутивности
5) Если в полученном ДНФ имеется несколько одинаковых конституент единицы, то оставляем только одну из них. В результате получается СДНФ.
Приведение КНФ к СКНФ:
1) Данную формулу приводим к КНФ
2) Если в дизъюнкт входит некоторая переменная вместе со своим отрицанием, то этот дизъюнкт удаляется из КНФ
3) Если в дизъюнкт одна и та же литера xδ входит несколько раз, то мы удаляем их все кроме одной
4) Если в некоторый дизъюнкт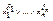 
не входит переменная y, то заменяем его на эквивалентную формулу 
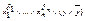и применяем закон дистрибутивности
5) Если в полученном КНФ имеется несколько одинаковых конституент нуля, то оставляем только одну из них. В результате получается СКНФ.
44. Импликанты , простые импликанты. Сокращенные, тупиковые, минимальные нормальные формы. Алгоритм Квайна построения МДНФ.