Если булева функция f и формула φ имеют одну и ту же таблицу истинности, то говорят, что формула φ представляет функцию f.
Булева функция также однозначно задается перечислением всех наборов, на которых она принимает значение 0, либо наборов, на которых она принимает значение 1.
Вектором значений булевой функции f ( x 1 ,…, xn ) называется упорядоченный набор всех значений функции f, при котором значений упорядочены по лексикографическому порядку множества аргументов {0,1} n.
Отметим, что поскольку всего имеется 2 n наборов нулей единиц, то существует ровно 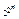 булевых функций от n переменных.
булевых функций от n переменных.
Наборы 0 и 1 можно представить в виде вершин n-мерных кубов или в виде вершин 2-дерева.
Функция f называется суперпозицией функций g ( y 1 ,.., yn ) и h 1 ( x 1 ,…, xn ),…, hm ( x 1 ,…, xn ), если f ( x 1 ,…, xn )= g ( h 1 ( x 1 ,…, xn ),…, hm ( x 1 ,…, xn )).
Булева функция, принимающая значения 1 (соответственно 0) на всех наборах нулей и единиц, называется константой 1 (константой 0).
Опишем булеву алгебру β n функцией алгебры логики от n переменных. В качестве носителя рассмотрим множество 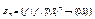 . Отношение ≤ на множестве Bn определим по следующему правилу:
. Отношение ≤ на множестве Bn определим по следующему правилу: 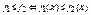 для любого набора значений X =(δ1,…,δ n ). Пересечением
для любого набора значений X =(δ1,…,δ n ). Пересечением 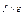 называется такая функция h , что h ( X )= min { f ( X ), g ( X )} на любом наборе X =(δ1,…,δ n ). Объединением
называется такая функция h , что h ( X )= min { f ( X ), g ( X )} на любом наборе X =(δ1,…,δ n ). Объединением 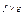 называется такая функция h, чтоh=max{f(X),g(X)} на любом наборе X. Дополнение функции f определяется следующим образом:
называется такая функция h, чтоh=max{f(X),g(X)} на любом наборе X. Дополнение функции f определяется следующим образом: 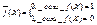 . В качестве 0 рассмотрим функцию, являющуюся константой 0, а в качестве 1 возьмем константу 1. Система
. В качестве 0 рассмотрим функцию, являющуюся константой 0, а в качестве 1 возьмем константу 1. Система 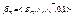 образует булеву алгебру функций от n переменных (алгебру булевых функций).
образует булеву алгебру функций от n переменных (алгебру булевых функций).
40. Эквивалентность формул.
Формулы φ ( x 1 ,…, xn ) и ψ ( x 1 ,…, xn ) называются эквивалентными (φ≈ψ), если совпадают их таблицы истинности, т.е. совпадают представляемые этими формулами функции.
Основные эквивалентности:
1) 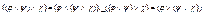 ассоциативность
ассоциативность
2) Коммутативность: 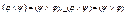
3) Идемпотентность: 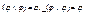
4) Дистрибутивность: 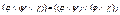 ,
, 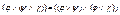
5) Поглощение: 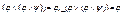
6) Законы де Моргана: 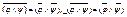
7) Двойное отрицание: 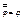
8) 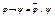
9) 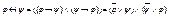
10) 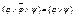
11) 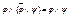
Формула φ ( x 1 ,…, xn ) называется выполнимой (опровержимой), если существует такой набор значений переменных, при котором формула принимает значения 1 (соответственно 0).
Формула φ ( x 1 ,…, xn ) называется тождественно истинной, или тавтологией (тождественно ложной, или противоречием), если эта формула принимает значение 1 (соответственно 0) при всех наборах значений переменных, т.е. функция fφ является константой 1 (константой 0).
Утверждения:
1) Формула φ тождественно ложна тогда и только тогда, когда ךφ тождественно истинна.
2) Формула φ опровержима тогда и только тогда, когда она не является тождественно истинной
3) Формула φ выполнима тогда и только тогда, когда она не является тождественно ложной.
Тождественно истинные (тождественно ложные) формулы образуют класс эквивалентности по отношению ≈.
Утверждение: Если формула φ1 тождественно истинна, φ0 – тождественно ложна, то справедливы следующие эквивалентности:
1) 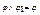 , 2)
, 2) 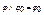 , 3)
, 3) 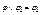 , 4)
, 4) 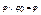 , 5)
, 5) 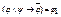 , 6)
, 6) 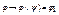 , 7)
, 7) 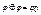 ,8)
,8) 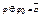 , 9)
, 9) 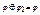 .
.
41. Двухэлементная булева алгебра. Алгебра булевых функций. Фактор-алгебра алгебры формул.
Опишем булеву алгебру β n функцией алгебры логики от n переменных. В качестве носителя рассмотрим множество 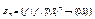 . Отношение ≤ на множестве Bn определим по следующему правилу:
. Отношение ≤ на множестве Bn определим по следующему правилу: 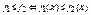 для любого набора значений X =(δ1,…,δ n ). Пересечением
для любого набора значений X =(δ1,…,δ n ). Пересечением 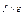 называется такая функция h , что h ( X )= min { f ( X ), g ( X )} на любом наборе X =(δ1,…,δ n ). Объединением
называется такая функция h , что h ( X )= min { f ( X ), g ( X )} на любом наборе X =(δ1,…,δ n ). Объединением 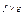 называется такая функция h, чтоh=max{f(X),g(X)} на любом наборе X. Дополнение функции f определяется следующим образом:
называется такая функция h, чтоh=max{f(X),g(X)} на любом наборе X. Дополнение функции f определяется следующим образом: 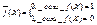 . В качестве 0 рассмотрим функцию, являющуюся константой 0, а в качестве 1 возьмем константу 1. Система
. В качестве 0 рассмотрим функцию, являющуюся константой 0, а в качестве 1 возьмем константу 1. Система 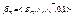 образует булеву алгебру функций от n переменных (алгебру булевых функций).
образует булеву алгебру функций от n переменных (алгебру булевых функций).
Рассмотрим множество B 0 ={0,1} и определим на нем операции 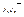 согласно таблицам истинности. Тогда система
согласно таблицам истинности. Тогда система 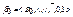 является двухэлементной булевой алгеброй. Формулы алгебры логики, содержащие лишь логические операции
является двухэлементной булевой алгеброй. Формулы алгебры логики, содержащие лишь логические операции 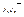 являются термами в β0. По теореме о функциональной полноте в булевой алгебре с помощью терма можно задать любую булеву функцию.
являются термами в β0. По теореме о функциональной полноте в булевой алгебре с помощью терма можно задать любую булеву функцию.
Обозначим через Ф n множество всех формул алгебры логики с переменными из множества { x 1 ,…, xn }. На множестве Ф n определены двухместные операции конъюнкции и дизъюнкции и одноместная операция отрицания. Выделим на множестве Ф n две константы 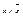 и
и 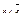 . Получается алгебра формул
. Получается алгебра формул 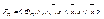 . Отношение ≈ эквивалентности формул является конгруенцией на алгебре множестве Ф n /≈ операции
. Отношение ≈ эквивалентности формул является конгруенцией на алгебре множестве Ф n /≈ операции 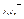 определяются следующим образом:
определяются следующим образом: 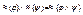 ,
, 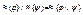 ,
, 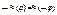 . На множестве Ф n /≈ выделяются две константы:
. На множестве Ф n /≈ выделяются две константы: 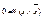 и
и 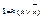 . Полученная система
. Полученная система 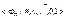 является фактор-алгеброй Fn /≈.
является фактор-алгеброй Fn /≈.
Теорема: Фактор-алгебра Fn /≈ изоморфна алгебре булевых функций βn.
Доказательство: Искомый изоморфизм 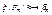 определяется по следующему правилу: классу эквивалентности ≈(φ) сопоставляется функция fφ, имеющая таблицу истинности произвольной формулы из множества ≈(φ). Поскольку разным классам эквивалентности соответствуют различные таблицы истинности, отображение ξ инъективно, а так как для любой булевой функции f из Bn найдется формула
определяется по следующему правилу: классу эквивалентности ≈(φ) сопоставляется функция fφ, имеющая таблицу истинности произвольной формулы из множества ≈(φ). Поскольку разным классам эквивалентности соответствуют различные таблицы истинности, отображение ξ инъективно, а так как для любой булевой функции f из Bn найдется формула 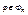 , представляющая функцию f, то отображение ξ сюръективно. Сохранение операций
, представляющая функцию f, то отображение ξ сюръективно. Сохранение операций 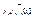 при отображении ξ проверяется непосредственно.
при отображении ξ проверяется непосредственно.
42. Дизъюнктивные и конъюнктивные нормальные формы. Алгоритм приведения формулы к ДНФ и КНФ.








