Если T1,…,Tn – упорядоченные деревья, то список (T1,…,Tn) называется упорядоченным лесом.
Для заданного упорядоченного дерева T определим множество S(T) его упорядоченных поддеревьев:
- если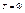 
, то 
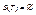
- если T =( a ), то S ( T )={( a )}
- если T =( a , T 1 ,…, Tn ), то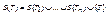 
Непустое упорядоченное дерево Т может интерпретироваться в виде системы пронумерованных непустых множеств, каждое из которых взаимно однозначно соответствует упорядоченному поддереву из S ( T ) так, что:
1) если T ’ – поддерево упорядоченного дерева T ’’;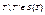 
, то для соответствующих множеств X ’ и X ’’ выполняется включение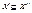 
2) если T ’ не является поддеревом упорядоченного дерева T ’’; 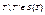, соответствующие множества не пересекаются.
Упорядоченное дерево может также интерпретироваться в виде уступчатого списка, который обычно используется в оглавлениях. Любая иерархическая классификационная схема интерпретируется некоторым упорядоченным деревом. Частным случаем упорядоченного дерева является бинарное дерево. Определение понятия бинарного дерева повторяет определение для упорядоченного дерева с ограничением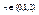 
в п.2. Любой упорядоченный лес взаимно однозначно соответствует некоторому бинарному дереву.
Опишем алгоритм преобразования упорядоченного леса T =( T 1 ,…, Tn ) в бинарное дерево B ( T ):
1) Если n=0,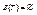 
2) Если n >0, то корнем бинарного дерева B(T) является корень упорядоченного дерева T 1, левое поддерево дерева B ( T ) – бинарное дерево B ( T 11 ,…, T 1 m ), где T 1 =(( a 1 ), T 11 ,…, T 1 m ), правое поддерево дерева B ( T ) – бинарное дерево B ( T 2 ,…, Tn).
36. Фундаментальные циклы, разрезы. Матрицы фундаментальных циклов, разрезов.
Пусть G =< M , R > - неорграф, имеющий n вершин, m ребер и c компонент связности, Т – остов графа G, имеет υ *( G )= n - c ветвей и υ ( G )= m - n + c хорд. Если к лесу T добавить произвольную хорду υ i, то в полученном графе найдется ровно один цикл Ci, который называется фундаментальным циклом графа G относительно хорды υ i и остова T. Множество { C 1 ,.., Cm - n + c } называется фундаментальным множеством циклов. Мощность этого множества равна цикломатическому числу υ ( G )= m - n + c.
Фундаментальное множество циклов можно задать с помощью матрицы фундаментальных циклов С=( aij ), где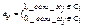 
. Т.к. каждый фундаментальный цикл содержит ровно одну хорду, то матрица С=(С1| C 2 ), где С1 – единичная матрица порядка υ ( G ).
Пусть G=<M,R> - неорграф, m={M1,M2} – разбиение множества М. Разрезом графа G по разбиению m называется множество всех ребер, соединяющих вершины из M1 c вершинными из M2. В связном графе любой разрез непуст.
Непустой разрез К неорграфа G называется простым разрезом или коциклом, если любое непустое собственное подмножество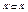 
не является разрезом ни по какому разбиению. Т.е. из К нельзя удалить ни одно ребро так, чтобы полученное множество было непустым разрезом.
Теорема: В связном неорграфе остовное дерево имеет по крайней мере одно общее ребро с любым из разрезов графа.
Теорема: В связном неорграфе любой цикл имеет любым разрезом четное число общих ребер.
Рассмотрим неорграф G с остовом Т. Пусть u1,…,un-c – ветви остова Т. Удаляя из Т произвольную ветвь ui получаем лес с (с+1) компонентой связности, т.е. каждое ребро ui является разрезом остова Т по некоторому разбиению {М1,М2}. В графе G могут найтись еще ребра vi1,…,vij (хорды Т), также являющиеся разрезами по {M1,M2}. Множество Ki={ui,vi1,…,vij} образует простой разрез, который называется фундаментальным разрезом графа G относительно ветви ui остова Т. Множество {K1,…,Kn-c} называется фундаментальным множество коциклов. Мощность этого множества равна корангу υ *( G )= n - c. Фундаментальное множество коциклов можно задать матрицей K=(bij), где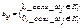 
. Поскольку каждый фундаментальный разрез содержит одну ветвь, то матрица К=(K1|K2), где К2 – единичная матрица порядка υ *( G ).
37. Раскраска графов. Планарные графы.
Пусть G =< M , R > - неорграф без петель. Раскраской (вершин) графа G называют такое задание цветов вершинам G, что если [ a , b ] – ребро, то вершины a и b имеют различные цвета. Хроматическим числом χ( G ) графа G называется минимальное число цветов, требующееся для раскраски графа G.
Раскраска ребер в мультиграфе G может быть определена с помощью раскраски вершин реберного мультиграфа L ( G ). Для произвольного неориентированного мультиграфа G =< M , U , P > реберным мультиграфом называется тройка L ( G )=< U , M , P ’>, где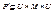 
, и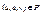 
тогда и только тогда, когда в мультиграфе G вершина u является концом ребер u и v.
Неорграф G называется бихроматическим, если χ ( G )=2. Неорграф G =< M , R > называется двудольным, если множество всех ребер графа G образует разрез графа G, т.е. для некоторого разбиения множества вершин { M 1 , M 2 } концы любого ребра принадлежат разным частям разбиения.
Теорема: Пусть G – неорграф без петель, имеющий хотя бы одно ребро. Тогда следующие условия эквивалентны:
1) G – бихроматический граф;
2) G – двудольный граф;
3) G не содержит циклов нечетной длины.
Следствие: Если G – лес, то χ ( G )≤2.
Теорема: Для любого неорграфа без петель выполняется неравенство χ ( G )≤ deg ( G )+1.
Алгоритм последовательной раскраски:
1) Произвольная вершина a 1 графа G принимает цвет 1.
2) Если вершины a 1 ,…, ai раскрашены l цветами 1,2,…, l , l ≤2, то новой произвольно взятой вершине ai +1 припишем миимальный цвет, не использованный при раскраске вершин из множества { aj |ρ( aj , ai +1 )=1, j < i }.
Неорграф G называется планарным, если его можно изобразить на плоскости так, что никакие два ребра не будут иметь общих точек, кроме, может быть, общего конца этих ребер. Такое изображение графа называется плоским.
Рассмотрим операцию подразбиения ребра в графе G =< M , R >. После подразбиения ребра [ a , b ] из R получается граф G ’=< M ’, R ’>, где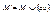 
, 
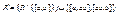, т.е. ребро [ a , b ] заменяется на ( a , b )-цепь длины два. Два графа называются гомеоморфными, если их можно получить из одного графа с помощью последовательности подразбиений ребер.
Критерий планарности (теорема Понтрягина-Куратовского): Граф G планарен тогда и только тогда, когда G не содержит подграфа, гомеоморфного K5 или K 3,3 (или подграфов, стягиваемых к K 5 или K 3,3, т.е. получаемых последовательным отождествлением связанных друг с другом вершин). 
Теорема: Любой конечный граф может быть расположен в трехмерном пространстве без пересечения ребер.
Если G – планарный граф, то χ ( G )≤4.
Толщина графа – минимальное количество плоскостей, в которых можно осуществить раскладку графа без пересечений.
Минимальное число ребер, которые нужно удалить из графа для его плоского отображения называют числом планарности графа.
38. Формулы алгебры логики, их таблицы истинности.
Высказыванием называется повествовательное предложение, о котором в данной ситуации можно сказать, что оно истинно или ложно, но не то и другое одновременно. Поставим в соответствие высказыванию Р логическую переменную х, которая принимает значение 1, если Р истинно, и 0, если Р ложно.
Определим по индукции понятие формулы алгебры логики:
1) Любая логическая переменная является формулой (атомарной);
2) Если φ и ψ – формулы, то выражения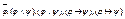 
являются формулами;
3) Никаких других формул, кроме построенных по пп 1, 2 нет.
Символы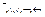 
называются логическими операциями или связками: отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность.
Действия логических операций задаются таблицами истинности, каждой строке которых взаимно однозначно соответствует набор значений переменных, составляющих формулу, и соответствующее значение полученной формулы:
| φ | ךφ | φ | ψ |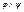 
| 
| 
| 
| |
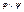
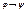
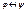
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 1 | 0 | 0 | |||
| 1 | 1 | 1 | 1 | 1 | 1 |
Другие логические операции:
1) 
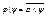штрих Шеффера, или антиконъюнкция;
2) 
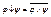стрелка Пирса, или антидизъюнкция;
3) 
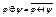кольцевая сумма или сложение по модулю 2.
| φ | ψ | φ|ψ |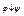 
| 
|
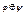
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 |
Некоторые соглашения о приоритете операций:
1) Внешние скобки не пишутся;
2) Вводится отношение:
| ך | ||
| | | ↓ |
| ||
| → | ||
| ↔ | 
|
Для равносильных связок расстановка скобок выполняется слева направо.
39. Булевы функции, способы их задания. Представления булевых функций формулами.
Функцией алгебры логики (ФАЛ) от n переменных x 1 ,…, xn называется любая функция f :{0,1} n →{0,1}, т.е. функция, которая произвольному набору {δ1,…,δ n } нулей и единиц ставит в соответствие значение f (δ1,…,δ n ) из {0,1}.
ФАЛ называются также булевыми функциями, двоичными функциями или переключательными функциями.
Булевой функцией описывается преобразование некоторым устройством входных сигналов в выходные.
Булева функция f ( x 1 ,…, xn ) полностью задается своей таблицей истинности. В каждой строке таблицы задается сначала набор значений переменных (δ1,…,δ n ), а затем значение функции на этом наборе.