Всякий максимальный по включению (сильно) связный подграф данного графа называется его (сильной) связной компонентой или (сильной) компонентой связности.

Дата: 2025-06-02; Просмотры: 20

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Теорема: Любой граф представляется в виде объединения непересекающихся связных (сильных) компонент. Разложение графа на связные (сильные) компоненты определяется однозначно.

Теорема: Если A_G – матрица смежности графа G, то (i,j)-й элемент матрицы 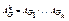есть число (a_i,a_j)-маршрутов длины k.

Следствие: 1) В графе G мощности n тогда и только тогда существует ( a_i , a_j )-маршрут ( a_i ≠ a_j ), когда ( i , j )-й элемент матрицы 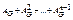не равен нулю.

2) В графе G мощности n тогда и только тогда существует цикл, содержащей вершину a_i, когда (i,i)-й элемент матрицы 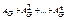не равен нулю.

Образуем из матрицы (b_ij)=E+A_G+A_G²+…+A_G^n-1 матрицу C=(c_ij) порядка n по следующему правилу: 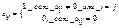. Матрица С называется матрицей связности, если G – неорграф, и матрицей достижимости, если G-орграф.

Определим матрицу контрдостижимости Q=(q_ij): 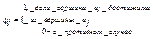. Причем Q=C^T.

Рассмотрим матрицу сильных компонент S=C*Q, где операция * означает поэлементное произведение матриц С и Q: s_ij=c_ij•q_ij. Таким образом, матрица S является матрицей отношения эквивалентности E: выполнимо a_iEa_j тогда и только тогда, когда a_i и a_j находятся в одной сильной компоненте.

30. Расстояние в графах. Центральные и периферийные вершины.

Пусть G=<M,R> - связный неорграф, a , b – две его несовпадающие вершины. Длина кратчайшего ( a , b )-маршрута называется расстоянием между вершинами a и b и обозначается ρ ( a , b ). Положим ρ ( a,a)=0.

Аксиомы метрики:

1) ρ ( a , b )≥0;

2) ρ ( a , b )=0 ó a=b

3) ρ ( a , b ) = ρ( b,a ) (симметричность)

4) ρ ( a , b )≤ ρ( a ,с)+ ρ(с, b ) (неравенство треугольника)

Если M ={ a ₁ ,…, a_n }, то матрица P =( p_ij ), в которой p_ij =ρ( a_i , a_j ), называется матрицей расстояний. Заметим, что P^T = P.

Эксцентриситетом вершины a называется величина .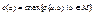

Максимальный среди всех эксцентриситетов вершин называется диаметром графа G и обозначается через d ( G ): 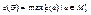. Вершина a называется периферийной, если e ( a )= d ( G ). Минимальный из эксцентриситетов графа G называется его радиусом r ( G ): 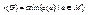. Вершина a называется центральной, если e ( a )= r ( G ). Множество всех центральных вершин графа называется его центром.

31. Взвешенное расстояние. Алгоритм Форда-Беллмана.

Пусть G =< M , R > - взвешенный граф, в котором вес каждой дуги ( a , b ) есть некоторое вещественное число μ ( a , b ). Весом маршрута a ₁ ,…, a_{n +1} называется число 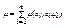. Взвешенным расстоянием (ω-расстоянием) ρ_ω ( a , b ) между вершинами a и b называется минимальный из весов ( a , b )-маршрутов). Маршрут с минимальным весом называется кратчайшим. Взвешенным эксцентриситетом вершины a называется величина 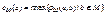. Взвешенной центральной вершиной называется вершина a, для которой 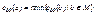. Взвешенный эксцентриситет центральной вершины называется взвешенным радиусом.

Пусть G =< M , R > - взвешенный граф, имеющий n вершин и матрицу весов W=(ω_ij). Предположим, что в G отсутствуют контуры с отрицательным весом, поскольку двигаясь по такому контуру достаточное число раз можно получить маршрут бесконечно малого веса.

Алгоритм Форда-Беллмана (для нахождения взвешенного расстояния от вершины a_i (источника) до всех вершин графа G):

Зададим строку 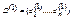, полагая 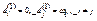. Определим строку 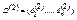, полагая 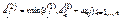. Нетрудно заметить, что 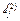- минимальный из весов ( a_i , a_j )-маршрутов, состоящих не более чем из двух дуг.

Продолжая процесс, на шаге s определим строку 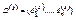, полагая 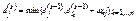. Искомая строка ω-расстояний получается при s=n-1: 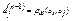. Алгоритм можно завершить на шаге k, если D^(k)=D^(k+1).

32. Степени вершин. Эйлеровы графы, циклы, цепи. Алгоритм построения эйлерова цикла.

Степенью или валентностью вершины a неорграфа G называется число ребер, инцидентных вершине a (петли считаются дважды). Вершина степени 0 называется изолированной, степени 1 – концевой или висячей.