При добавлении или удалении вершин графа, удобно представить его в в виде структуры смежности, получаемой составлением для каждой вершины a списка номеров ее последователей.
28. Подграфы и части графа. Операции над графами. n -Мерные кубы.
Граф G’=<M’,R’> называется подграфом графа G=<M,R>, если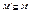 
и 
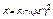. Граф G’ называется частью графа g, есл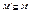и и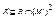 
.
Операции над графом G =< M , R >:
1) Добавление вершины: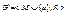 
2) Добавление дуги: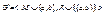 
3) Удаление вершины: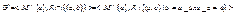 
4) Удаление дуги: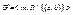 
5) Отождествление вершин: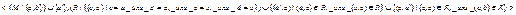 
6) Дополнением графа без петель G=<M,r> называется граф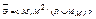 
.
Двухместные операции над графами G1=<M1,R1>, G2=<M2,R2>:
1) Объединение: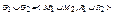 
.
2) Пересечение: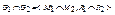 
, если 
.
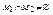3) Кольцевая сумма: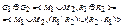 
.
4) Соединение: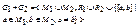 
5) Произведени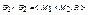е: 
, где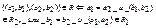 
6) Композиция: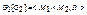 
, где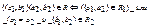 
. Т.е. каждая вершина a графа G1 заменяется на изоморфную копию Ga графа G2, а затем, если 
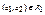, то между любыми вершинами b1 из Ga1 и b2 из Ga2 проводится дуга (b1,b2).
Неорграф без петель называется полным, если его любые две различные вершины смежны. Полный граф, имеющий n вершин обозначается Kn.
Определим по индукции важный класс графов, называемых n-мерными кубами. Рассмотрим граф K2, вершины которого обозначим 0 и 1. n-куб Qn определяется по следующим правилам: Q1=K2,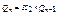 
, n>1. Вершинами n-куба являются всевозможные n-ки, состоящие из наборов нулей и единиц (всего таких наборов 2n), а ребра задаются по следующему правилу: вершины смежны тогда и только тогда, когда соответствующие кортежи различаются ровно одной координатой.
29. Маршруты, циклы, цепи. Достижимость и связность (матрицы достижимости, контрдостижимости, связности).
Пусть G=<M,R> - граф. Последовательность a 1 , u 1 , a 2 , u 2 ,…, un , an +1, где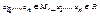 
, называется маршрутом, соединяющим вершины a 1 и an +1, если ui =( ai , ai +1 ). Число n дуг в маршруте называется его длиной.
Пусть G – неорграф. Маршрут ( a 1 , an +1 ) называется цепью, если все ребра [ a 1 , a 2 ],…,[ an , an +1 ] различны, и простой цепью, если все его вершины, кроме, возможно, первой и последней, различны. Маршрут называется циклическим, если a 1 = an +1. Циклическая цепь называется циклом, а циклическая простая цепь – простым циклом.
Пусть G – орграф. Маршрут называется путем, если все его дуги различны. Путь называется контуром, если a 1 = an +1. Граф, не имеющий контура, называется бесконтурным. Вершина b называется достижимой из вершины a, если существует ( a , b ) – путь.
Неорграф называется связным, если любые две его несовпадающие вершины соединены маршрутом. Граф G называется связным, если соответствующий ему неорграф F(G) тоже является связным. Граф G называется сильно связным, если для каждой пары различных вершин a и b существуют (a,b)-маршрут и (b,a)-маршрут. Аналогично определяются понятия связности и сильной связности для мультиграфов.