Граф G называется неориентированным (неорграфом), если отношение R симметрично, т.е. из следует .

Дата: 2025-06-02; Просмотры: 18

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Если одновременно пары ( a , b ) и ( b , a ) принадлежат R, то информацию об этих дугах можно представить множество [ a , b ]={( a , b ),( b , a )}, называемым ребром, соединяющим вершины a и b.

Понятия морфизмов алгебраических систем для графов представляются следующим образом. Пусть G =< M , R >, G ’=< M ’, R ’> - графы. Тогда отображения φ = M → M ’ является изоморфизмом графов, если .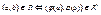

Информация о структуре графа может быть задана матрицей бинарного отношения. Пусть G =< M , R > - граф, в котором множество вершин имеет n элементов M ={ a ₁ ,…, a_n }. Матрицей смежности A_G =( A_ij ) графа G называется матрица порядка n, определенная следующим образом: 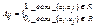. Если A_ij =1, то вершина a_j называется последователем вершины a_i, а a_i – предшественником a_j . Вершины a_i и a_j называются смежными, если A_ij =1 или A_ji =1. Если G -мультиграф, то в матрице смежности элемент A_ij равен числу дуг, исходящих из вершины a_i и заходящих в вершину a_j.

Петлей в графе G называется дуга, соединяющая вершину саму с собой.

Теорема: Графы изоморфны тогда и только тогда, когда их матрицы смежности получаются друг из друга одновременными перестановками строк и столбцов.

Матрицей инцидентности B_G=(B_ij) мультиграфа G называется матрица размера m на n (где m – количество дуг в графе), определяемая по правилу: .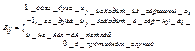

Теорема: Мультиграфы G и G’ изоморфны тогда и только тогда, когда их матрицы инцидентности получаются друг из друга некоторыми перестановками строк и столбцов.

Пометкой или распределением меток графа G=<M,R> называется пара функций f:M→S_M (распределение меток вершин), g:R→S_R (распределение меток дуг). Четверка <M,R,d,g> называется взвешенным или помеченным графом.

Информацию о весах дуг во взвешенном графе можно представить в виде матрицы весов W=(w_ij), где w_ij – вес дуги (a_i,a_j), если эта дуга существует и ∞ в противном случае.

Если граф G =< M , R > является разреженным, т.е. | R |<<| M |, то можно задать граф в виде списка дуг: два набора 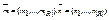, где ( a_mi , a_ni ) – i-ая дуга графа G.