Пусть - булева алгебра. Определим операции кольцевых сложения и умножения на β по следующим правилам: - соответствует кольцевой сумме множеств, - соответствует пересечению множеств.

Дата: 2025-06-02; Просмотры: 10

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Теорема: Система 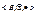образует булево кольцо с единицей 1.

Тогда: , , .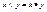

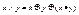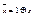18. Алгебры отношений. Реляционные алгебры.

Рассмотрим алгебру отношений, носителем которой является множество отношений K={P₁,…,P_m,…}, а сигнатура ∑ состоит из символов частичных двухместных операций объединения 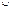, пересечения 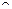, разности \ и декартова произведения отношений.

Отношения P_i и P_j называются совместимыми, если 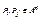для некоторого множества А и числа n из ω.

Объединением 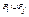двух совместимых отношений P_i и P_j называется множество всех кортежей, каждый из которых принадлежит хотя бы одному из этих соотношений: 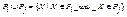. Пересечением 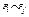двух совместимых отношений P_i и P_j называется множество всех кортежей, принадлежащих как отношению P_i, так и отношению P_j: 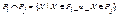. Разностью P_i\P_j двух совместимых отношений P_i и P_j называется множество всех кортежей, принадлежащих отношению P_i и не принадлежащих отношению P_j: 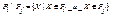. Декартовым произведением 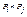двух отношений P_i и P_j называется множество всех кортежей z таких, что z – конкатенация кортеже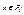й и 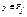: z=x^y, где x^y=(x₁,…,x_r,y₁,…,y_a), если x=(x₁,…,x_r), y=(y₁,…,y_s). Т.е. .

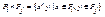Алгебры отношений находят применение при реализации формальных объектов. Рассмотрим, как используется алгебра отношений при создании информационного обеспечения – разработки реляционной базы данных. Основой построения реляционной базы данных является двумерная таблица, каждый i-ый столбец которой соответствует i-ому домену (если n-местное отношение R_n содержится в 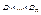, то i-м доменом отношения R_n, где i=1,…,n, называется множество D_i), строка – кортежу значений доменов, находящихся в отношении R_n. Т.е. каждому отношению можно поставить в соответствие таблицу.

Для преобразования отношений определим реляционную алгебру. Носитель реляционной алгебры представляет собой множество отношений K, а набор операций кроме введенных операций 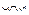включает специальные операции над отношениями: выбор, проекцию и соединение.

Операция выбора представляет собой процедуру построения «горизонтального» подмножества отношения, т.е. подмножества кортежей, обладающих заданным свойством.

Результатом операции проекции отношения 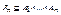на A_i1,…,A_im, где 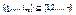, i_j<i_k при j<k, называется множество 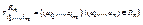. Операция проекции определяет построение «вертикального» подмножества отношения, т.е. из кортежей удаляются координаты, соответствующие невыделенным доменам.

Операция соединения по двум таблицам, имеющим общий домен, позволяет построить одну таблицу, каждая строка которой образуется соединением двух строк исходных таблиц. Из заданных строк берут строки, содержащие одно и то же значение общего домена; общему домену ставится в соответствие один столбец.

27. Виды и способы задания графов.

Графом называется алгебраическая система G =< M , R >, где R – двухместный предикатный символ. Элементы носителя М называются вершинами графа G, а элементы бинарного отношения 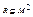- дугами. Таким образом, дугами являются пары вершин 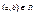. При этом дуга ( a , b ) называется исходящей из вершины a и заходящей в вершину b.

Мультиграфом G называется тройка < M , U , P >, в которой M – множество вершин, U – множество дуг, а 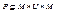- трехместный предикат, называемый инцидентором и представляемый следующим образом: 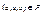тогда и только тогда, когда дуга u исходит из вершины a и заходит в вершину b.

Граф G =< M , R > называется ориентированным (орграфом), если найдется дуга 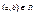такая, что .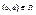