Если φ: α→β – гомоморфизм алгебр, то множество оказывается конгруэнцией на алгебре α и называется ядром гомоморфизма φ.
Теорема о гомоморфизме: Если φ: α→β – эпиморфизм, ψ: α→α/Kerφ – естественный гомоморфизм, то существует изоморфизм χ: β→α/Kerφ такой, что φ•χ=ψ.
Доказательство: Положим χ ( b )=ψ( a ), где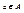 
выбрано так, что b =φ( a )/ Если b =φ( a ’), то 
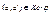, откуда ψ ( a )=ψ( a ’). Следовательно, отображение χ определяется корректно. Равенство φ•χ=ψ очевидно. Из него вытекает, что χ – сюръекция. Непосредственно проверяется, что χ – гомоморфизм. Если χ ( b )= χ ( b ’), то ψ ( a )= ψ ( a ’), где b=φ(a), b’=φ(a’). Отсюда 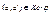, следовательно b=b’, что доказывает возможную однозначность отображения χ. Т.к. сигнатура функциональна, из существования функции χ-1 и того, что χ – гомоморфизм, следует, что χ является изоморфизмом.
Отображения φ, ψ и χ можно представить диаграммой:
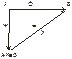
17.Многообразия. Теорема Биркгофа.
Пусть Ai,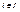 
- семейство множеств. Декартовым произведением множеств Ai, 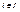называется множество
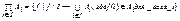Отметим, что если I={1,2,…,n} – конечное множество индексов, то декартово произведение 
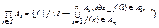можно взаимно однозначно рассматривать как множество 
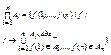. Таким образом данное определение согласуется с введенным ранее определением декартова произведения конечного числа множеств.
Пусть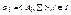 
- некоторые алгебры сигнатуры ∑. Декартовым произведением алгебр 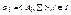называется алгебра 
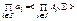, в которой функциональные символы 
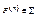интерпретируются по следующему правилу: для любых функций 
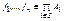полагаем F(f1,…, fn)=f, где f(i)=Fαi(f1(i),…,fn(i)) для любого 
.
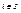Пусть t1, t2 - термы сигнатуры ∑. Запись t1≈t2 называется тождеством сигнатуры ∑. Она означает, что любые значения, вычисленные по терму t1, совпадают с соответствующими значениями, вычисленными по терму t2.
Класс К алгебр сигнатуры ∑ называется многообразием, если существует множество тождеств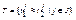 
сигнатуры ∑ такое, что алгебра сигнатуры ∑ принадлежит классу К тогда и только тогда, когда в ней выполняются все тождества из множества Т.
Теорема Биркгофа: Непустой класс алгебр К сигнатуры ∑ тогда и только тогда является многообразием, когда К замкнут относительно подалгебр, фактор-алгебр и декартовых произведений, т.е. класс К вместе с каждой алгеброй содержит любую ее подалгебру, фактор-алгебру, а также вместе с любым семейством алгебр содержит их декартово произведение.
14. Решетки. Дистрибутивные решетки. Критерий дистрибутивности.
Элемент 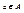называется точной верхней гранью (супремумом) множества В (обозначается supB), если а – наименьшая из всех верхних граней множества В. Элемент 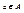называется точной нижней гранью (инфимумом) множества В (обозначается infB), если а – наибольшая из всех нижних граней множества В.
Решеткой называется ЧУМ α=<A,≤>, в котором каждая пара элементов имеет супремум и инфимум. Для заданных элементов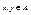 
элемент inf{x,y} называется пересечением элементов x и y ( 
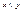), а sup{x,y} называется объединением элементов x и y ( 
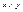). Заметим, что тогда 
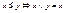и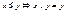 
. Наибольший (наименьший) элемент решетки, если он существует, называется нулем (единицей). В конечных решетках всегда есть нуль и единица.
Определим решетку подсистем системы β=<B,∑>, содержащих непустое множество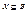 
. Рассмотрим множество 
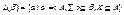и зададим на нем частичный порядок ≤ по следующему правилу: 
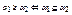. Пара <L(β),≤> образует решетку подсистем. В этой решетке для любых систем α1=<A1,∑>, α2=<A2,∑> из L(β) пересечение 
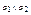есть подсистема 
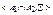, а объединение 
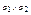- подсистема, порожденная множеством 
.
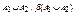Пусть α=<A,∑> - алгебра, Conα={θ | θ – конгруэнция на α}. На множестве конгруэнций Conα зададим отношение ≤ по следующему правилу: θ1≤θ2 <=> для любых элементов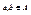 
из условия aθ1b вытекает aθ2b. Это означает, что каждый θ2-класс состоит из θ1-классов. Система <Conα,≤> образует решетку конгруэнций. В этой решетке: для любых 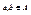тогда и только тогда 
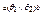, когда aθ1b и aθ2b; для любых 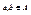тогда и только тогда 
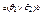, когда существуют такие 
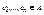, что c1=a, cn=b и справедливо ciθ1ci+1 или ciθ2ci+1 для любого i=1,…, n-1. Решетка конгруэнций имеет нулевую конгруэнцию 
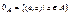и единичную конгруэнцию 1A=A2.
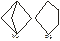Решетка α=<A,≤> называется дистрибутивной, если она подчиняется дистрибутивным законам 
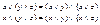для всех 
.
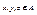Недистрибутивные решетки:
Критерий дистрибутивности: Решетка α=<A,≤> дистрибутивна тогда и только тогда, когда она не имеет подрешеток, изоморфных М3 или Р5.
15. Булевы алгебры. Теорема Стоуна. Принцип двойственности для булевых алгебр.
Дистрибутивная решетка α=<A,≤> называется булевой алгеброй, если α имеет нуль0, единицу 1, 0≠1 и для любого элемента х из А найдется элемент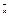 
(дополнение х) такой, что 
, 
.
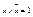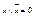Утверждение: Если α=<A,≤> - булева алгебра, то для любого элемента х дополнение 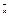единственно.
Доказательство: Предположим, что элемент х имеет два дополнения y и z, т.е.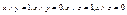 
. По закону дистрибутивности получим, что элементы 
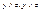также являются дополнениями х, т.е. 
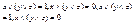. При этом из y≠z следует, что 
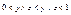. Отсюда получаем, что подрешетка решетки α с носителем 
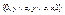образует решетку Р5, что противоречит дистрибутивности решетки α. Наше допущение неверно.
Свойства булевой алгебры:
1) Ассоциативность: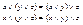 
2) Коммутативность: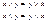 
3) Идемпотентность: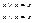 
4) Дистрибутивность: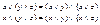
5) Поглощение: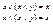 
6) Законы де Моргана: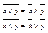 
7) Законы нуля и единицы: 0=ø, 1=U
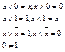
8) Закон двойного отрицания: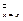 
Теорема Стоуна: Любая конечная булева алгебра изоморфна некоторой алгебре Кантора (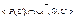 
)
Следствие: Любые две булевы алгебры, имеющие одинаковое число элементов, изоморфны. Число элементов конечной булевой алгебры равно 2n для некоторого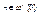 
.
Таким образом, конечная булева алгебра определяется однозначно с точностью до изоморфизма числом своих элементов.
Принцип двойственности для булевых алгебр: если в справедливом утверждении о булевых алгебрах, касающемся отношения ≤ и операций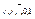 
, всюду заменить на 
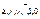соответственно, то получится также справедливое утверждение, называемое двойственным к исходному.
16. Булево кольцо.
Кольцо <R,+,•> называется булевым, если a 2 = a для всех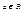 
.
Утверждение: Булево кольцо коммутативно, и a + a =0 для всех элементов .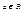
Доказательство: По определению булева кольца: a+a=(a+a)2=a2+a2+a2+a2=a+a+a+a. Отсюда a+a=0, т.е. a=-a. Также, a+b=(a+b)2=a2+ab+ba+b2=a+b+ab+ba. Отсюда ab+ba=0. Тогда ab=ab+(ba+ba)=(ab+ba)+ba=ba.
Единицей кольца R называется такой элемент e, что a • e = e • a = a , для всех 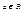.