Подсистема β(Х) из данной теоремы называется подсистемой, порожденной множеством Х в β. Она является наименьшей подсистемой системы β, содержащей множество Х.
Для описания устройства подсистемы β(Х) определим индукцией понятие терма сигнатуры ∑:
1) переменные и константные символы из ∑ есть суть термы
2) если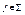 
- n-местный функциональный символ, t1,…, tn – термы, то f(t1,… tn) – терм
3) никаких термов, кроме построенных по пп. 1,2, нет.
Таким образом, термом является любое функциональное выражение, составленное с помощью сигнатурных функциональных символов. Множество всех термов сигнатуры ∑ обозначается через Т(∑).
Пусть t(x1,…, xk) – терм из Т(∑), все переменные которого содержаться среди x1,…, xk; α=<A,∑> - алгебраическая система. Значение терма t при значениях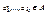 
переменных x1,…, xk (t(a1,..., ak)) определяется по индукции:
1) если t – переменная xi (константный символ с), то значение t есть ai (c).
2) если терм t есть f(t1,…, tn), а t1(a1,…, ak)=b1,…, tn(a1,…, ak)=bn, то t(a1,…, ak)=b(t1,…, tn)
Теорема (о структуре подсистемы, порожденной множеством): Если β=<B,∑> - алгебраическая система,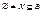 
, то носитель подсистемы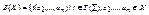 
Доказательство: Индукцией по числу шагов построения терма t получаем, что если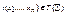 
и 
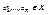, то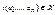 
для любой подсистемы 
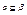, содержащей Х. Поэтому достаточно показать, что множество 
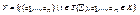замкнуто относительно операций системы β. Пусть 
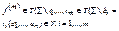. Тогда 
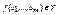, поскольку 
.
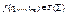Таким образом, носитель подсистемы β(Х) состоит из всех элементов, которые получаются при подстановке элементов из Х в термы.
13. Конгруэнции, фактор-алгебры, теорема о гомоморфизме.
Конгруэнцией на алгебре α=<A,∑> называется такое отношение эквивалентности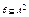 
, при котором для любого 
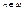, любого n-местного символа 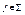, произвольных наборов 
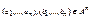, если a 1 θ b 1 ,…, anθbn, то f ( a 1 ,…, an )θ f ( b 1 ,…, bn ). Т.е. все операции согласованы с отношением эквивалентности.
Рассмотрим фактор-множество множества А по конгруэнции θ: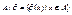 
. Определим на этом множестве алгебру сигнатуры ∑. Константе с алгебры А поставим в соответствие элемент θ(с), который в А/θ будет интерпретировать константный символ с. Если f – n-местный символ из ∑, то зададим на множестве А/θ действие функции f по правилу:
f ( θ ( x 1 ),…, θ ( xn ))= θ ( f ( x 1 ,…, xn )).
Убедимся, что для любых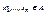 
это определение корректно, т.е. не зависит от выбора представителей классов эквивалентности. Действительно, если θ ( xi )= θ ( yi ), i =1,2,…, n, то xiθyi, откуда в силу свойства конгруэнции имеем f ( x 1 ,…, xn )θ f ( y 1 ,…, yn ), т.е. θ ( f ( x 1 ,…, xn ))= θ ( f ( y 1 ,…, yn )).
Получившаяся алгебра α /θ=< A /θ,∑> называется фактор-алгеброй алгебры α по конгруэнции θ.
Очевидно, что отображение А→А/θ, при котором элементу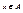 
ставится в соответствие класс θ(х), является эпиморфизмом алгебры α на фактор-алгебру α/θ. Этот эпиморфизм называется естественным гомоморфизмом.