Частичный порядок ≤ на множестве А называется линейным порядком, если любые два элемента x и y из множества А сравнимы, т.е. x≤y или y≤x.

Дата: 2025-06-02; Просмотры: 11

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Линейный порядок ≤ на множестве А называется полным, если каждое непустое подмножество множества А имеет наименьший элемент. Пара <A,≤>, в которой отношение ≤ является полным порядком на множестве А, называется вполне упорядоченным множеством.

10. Алгебраические системы: определение и примеры. Понятие полугруппы, моноида, группы; задание с помощью таблицы Кэли.

Алгебраической системой A=<A,∑> называется пара, где А – непустое множество, носитель алгебраической системы; ∑ - сигнатура алгебраической системы, множество функциональных и предикатных символов с указанием их местности. Примеры: <ω, +⁽²⁾, •⁽²⁾, ≤⁽²⁾, 0⁽⁰⁾, 1⁽⁰⁾>; <R, +⁽²⁾, -⁽²⁾, e⁽⁰⁾>

Сигнатура ∑ называется функциональной (предикатной), если она не содержит предикатных (функциональных) символов. Система А называется алгеброй (моделью), если ее сигнатура функциональна (предикатна).

Группоид – алгебраическая система с одной двухместной операцией. Эта единственная операция часто обозначается символом •. Если А – конечное множество, то действия операции • можно задать квадратной таблицей, в которой для каждой пары 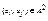записан результат действия. Такая таблица называется таблицей Кэли группоида А. (Что-то наподобие таблицы умножения).

Полугруппа – группоид, у которого операция • ассоциативна. Т.е. x•(y•z)=(x•y) •z/

Моноид – полугруппа, для которой существует элемент e называемый единицей, такой, что e•x=x•e=x.

Группа – моноид, в котором для любого элемента 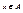существует элемент 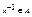, называемый обратным к x, такой, что x•x^-1=x^-1•x=e.

Группа называется коммутативной или абелевой, если x•y=y•x.

11. Морфизмы алгебраических систем.

Пусть даны алгебраические системы: α=<A,∑>, β=<B,∑>. Отображение φ: А→В называется гомоморфизмом системы α в систему β, если выполняются следующие условия:

1) 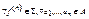должно выполняться согласование для функциональных символов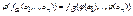

2) 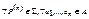должно выполняться согласование предикатных символов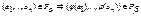

Если φ: А→В – гомоморфизм, то будем писать φ: α→β.

При гомоморфизме сохраняются действия операций и отношения.

Гомоморфизм φ: α→β, являющийся инъекцией, называется мономорфизмом (т.е. )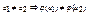

Гомоморфизм φ: α→β, являющийся сюръекцией, называется эпиморфизмом, и при этом система β называется гомоморфным образом системы α.

Сюръективный мономорфизм φ: α→β, для которого φ^-1 – гомоморфизм, называется изоморфизмом (φ: α≈β).

Изоморфизм φ: α→α называется автоморфизмом системы α.

Утверждения:

1) id_A: α≈α (Рефлексивность)

2) если φ: α≈β, то φ^-1: β≈α (симметричность)

3) если φ: α≈β и ψ: β≈γ, то φ•ψ: α≈γ (транзитивность)

12. Подсистемы. Термы сигнатуры ∑. Подсистема, порожденная множеством, ее структура.

Алгебраическая система α=<A,∑> называется подсистемой системы β=<B,∑>, если выполняются следующие условия:

1)

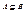
2) для любого функционального символа 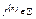, соответствующих функций 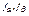и любых элементов 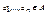выполняется равенство f_α(a₁,…, a_n) = f_β(a₁,…, a_n), т.е интерпретации символа f действуют одинаково на элементах из А

3) для любого предикатного символа 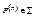, соответствующих предикатов Р_α, Р_β справедливо равенство 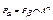, т.е. предикат Р_α содержит в точности те кортежи отношения Р_β, которые состоят из элементов множества А.

Если ∑ - функциональная (предикатная) сигнатура, то подсистема α алгебры (модели) β называется подалгеброй (подмоделью).

Теорема: Если β – алгебраическая система, 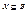, , 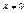то существует единственная подсистема 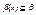с носителем В(Х), такая, что 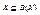и 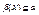для любой подсистемы 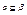, для которой .

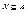Доказательство: В качестве В(Х) рассмотрим пересечение носителей А всех подсистем 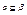, содержащих Х. Т.к. 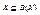, то 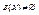. Единственность подсистемы β(Х) очевидна.