Отношение Р называется отношением эквивалентности, если Р рефлексивно, симметрично и транзитивно. Обозначается Е и ~ (тильда).
Пусть Е – эквивалентность на множестве А. Классом эквивалентности элемента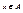 
называется множество E(x)={y | xEy}. Классы эквивалентности Е также называют Е-классами. Множество 
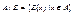называется фактор-множеством множества А по отношению к Е.
Утверждение: Множество всех классов эквивалентности образует разбиение множества А (система непересекающихся подмножеств, объединение которых совпадает с А). Если {Ai} – некоторое разбиение множества А, то по этому разбиению можно однозначно определить эквивалентность. Т.е. xEy тогда и только тогда, когда x, y принадлежат Аi для некоторого i.
Доказательство:
Пусть Е – отношение эквивалентности на множестве А, А/Е – фактор-множество множества А по Е. Т.к. в силу рефлексивности Е выполнимо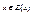 
для любого 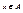, то каждое множество из А/Е непустое и 
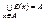. Чтобы установить, что А/Е – разбиение множества А, покажем, что если 
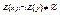, то E(x)=E(y).
Пусть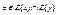 
и 
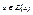, т.е. 
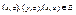. Т.к. Е симметрично, то 
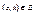. Из транзитивности Е следует 
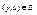, т.е. 
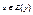. Таким образом, 
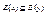. Обратное включение доказывается аналогично.
Предположим, что Е – отношение на множестве А, соответствующее разбиению R={Ai}. Рефлексивность и симметричность Е очевидны. Пусть выполняется xEy и yEz. Тогда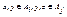 
, где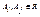 
. Поскольку 
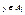и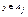 
, то Аi=Aj. Следовательно Е транзитивно. Е – эквивалентность.
Матрица отношения эквивалентности имеет блочно-диагональный вид. Или приводится к нему путем одновременных перестановок строк и столбцов.
9. Отношения порядка. Максимальные и минимальные, наибольший и наименьший элементы частично упорядоченного множества. Диаграммы Хассе. Линейно и вполне упорядоченные множества.
Отношение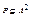 
называется предпорядком или квазипорядком, если Р рефлексивно и транзитивно.
Отношение 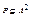называется частичным порядком, если Р рефлексивно, транзитивно и антисимметрично. Т.е. частичный порядок – это антисимметричный предпорядок.
Множество, с заданным на нём частичным порядком называется частично упорядоченным множеством (ЧУМ)
Пусть <A,≤> - ЧУМ. Тогда элемент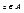 
называется наибольшим, если 
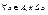. Элемент 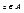называется наименьшим, если 
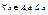. Элемент 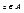называется максимальным, если для него нет большего, т.е. 
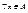, если 
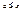, то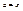 
. Элемент 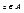называется минимальным, если для него нет меньшего, т.е. 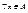, если 
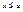, то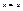 
.
Наименьший элемент всегда минимален (наибольший – максимален). Обратное неверно.
Наибольший элемент часто называют единицей. Наименьший – нулем.
Диаграммы Хассе:
Рассмотрим ЧУМ <A,≤>. Говорят, что элемент y покрывает элемент x, если x≤y и x≠y не существует такого элемента z, что x<z<y. Если множество А конечно, то частично упорядоченное множество <A,≤> можно представить в виде схемы, в которой каждый элемент изображается точкой на плоскости, и если y покрывает х, то точки х и y соединяются отрезком, причем точку х располагают ниже y. Такие схемы называются диаграммами Хассе.