Мощности множеств также иногда называют кардинальными числами.
1. Множества. Основные операции над множествами и их свойства. Диаграммы Венна. Декартово произведение множеств.
Множество – это совокупность объектов, рассматриваемых как единое целое.
Способы задания множеств:
1) Перечисление элементов: М={0,1,2,…,9}
2) Указание свойств Р(х), которым элементы множества должны удовлетворять: М={x | P(x)}.
Неправильное заданные свойства могут привести к противоречию!
Парадокс Рассела:
Рассмотрим множество всех множеств, которые не являются своими собственными элементами: 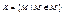 . Является ли тогда множество К своим элементом. Если КєК, то должно выполняться свойство, задающее множество К, т.е. К¢К, что приводит к противоречию. Если же К¢К, то, поскольку выполняется свойство, задающее К, то КєК, а это противоречит предположению. Таким образом, не всякое свойство приводит к осмысленному заданию множества.
. Является ли тогда множество К своим элементом. Если КєК, то должно выполняться свойство, задающее множество К, т.е. К¢К, что приводит к противоречию. Если же К¢К, то, поскольку выполняется свойство, задающее К, то КєК, а это противоречит предположению. Таким образом, не всякое свойство приводит к осмысленному заданию множества.
Множество А называется подмножеством множества В, если все элементы А принадлежат В, т.е. 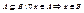
Множества А и В называются равными или совпадающими, если они состоят из одних и тех же элементов, т.е. 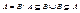
Совокупность всех подмножеств множества А называется его булеаном или множеством-степенью и обозначается Р(А), т.е. 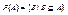 . Если |U|=n (множество U содержит n элементов), то |P(U)|=2n.
. Если |U|=n (множество U содержит n элементов), то |P(U)|=2n.
Множество, не содержащее ни одного элемента называется пустым ø.
Множество, содержащее все элементы, находящиеся в рассмотрении, называется универсальным или универсумом U.
Операции над множествами:
1) объединение 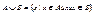
 2) пересечение
2) пересечение 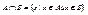
3) вычитание 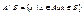
4) кольцевая сумма (симметрическая разность) 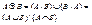
5) дополнение 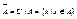
Свойства основных операций над множествами:
1) Ассоциативность: 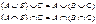
2) Коммутативность: 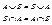
3) Идемпотентность: 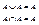
4) Дистрибутивность: 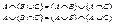
5) Поглощение: 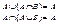
6) Законы де Моргана: 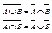
7) Законы нуля и единицы: 0=ø, 1=U
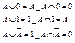
8) Закон двойного отрицания: 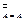
Упорядоченную последовательность (х1, х2,…,хn) называют кортежем длины n.
Декартовым (прямым) произведением множеств А1, А2,…, Аn называется множество {(x1, x2,…, xn) | x1 є A1,…, xn є An}.
Если А1=А2=…=Аn, то 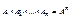 – n-ная декартова степень множества А.
– n-ная декартова степень множества А.
А0 = ø
2. Отношения и бинарные отношения, область определения, область значения, обратные отношения. Произведение отношений.
n -местным отношением или n -местным предикатом Р на множествах А1, А2,…, Аn называется любое подмножество прямого произведения 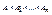 . Другими словами, элементы х1, х2,…, хn (где хi є Ai) связаны соотношением Р тогда и только тогда, когда (х1, х2,…, хn) є Р. При n=1 отношение Р является подмножеством множества А1 и называется унарным отношением или свойством.
. Другими словами, элементы х1, х2,…, хn (где хi є Ai) связаны соотношением Р тогда и только тогда, когда (х1, х2,…, хn) є Р. При n=1 отношение Р является подмножеством множества А1 и называется унарным отношением или свойством.
При n=2 отношение Р называется бинарным отношением или соответствием. 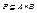
Пример: Если А={2,3,4,5,6,7,8}, то бинарное отношение Р={(x,y) | x,y є A, x делит y и х≤3} можно записать в виде Р = {(2,2),(2,4),(2,6),(2,8),(3,3),(3,6)}.
Если Р={(x, y) | x, y є R, x≤y}, то запись xPy означает, что x≤y. idA = {(x,x) | x є A} – тождественное отношение, idA принадлежит А2.
U = A2 – универсальное отношение. Пусть Р – некоторое бинарное отношение. Областью определения отношения Р называется множество δР = {x | (x,y) є P для некоторого у}. Областью значений отношения Р называют множество ρР = {y | (x,y) є P для некторого х}. Обратным отношением называется множество Р-1 = {(y,x) | (x,y) є P}.
Образом множества Х относительно предиката Р называется множество Р(Х)={y | (x,y) є P для некоторого х є Х}
Прообразом множества относительно предиката Р называется множество Р-1(Х) или, другими словами, образ множества Х относительно предиката Р-1.
Произведением бинарных отношений 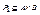 и
и 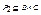 или композицией Р1 и Р2 называется множество Р1•Р2 = {(x,y) | x є A, y є C, и найдется элемент z є B такой, что (x,z) є Р1 и (z,y) є P2}.
или композицией Р1 и Р2 называется множество Р1•Р2 = {(x,y) | x є A, y є C, и найдется элемент z є B такой, что (x,z) є Р1 и (z,y) є P2}.
Свойства:
1) Ассоциативность композиции: (P•Q)•R=P•(Q•R)
Доказательство: Пусть (x,y) є (P•Q)•R. Тогда для некоторых u и v имеем (x,u) є P, (u,v) є Q, (v,y) є R. Тогда (u,y) є Q•R и (x,y) є P•(Q•R). Включение P•(Q•R) є (P•Q)•R доказывается аналогично.
2) (P•Q)-1=Q-1•P-1
Доказательство: Предположим, что (x,y) є (P•Q)-1. Тогда (y,x) є P•Q, и, следовательно, (y,z) є P и (z,x) є Q для некоторого элемента z. Значит (x,z) є Q-1, (z,y) є P-1 и тогда (x,y) є Q-1•P-1. Обратное включение доказывается аналогично.
3) P•Q ≠ Q•P
4) (P-1)-1=P
Доказательство: Если (x,y) є P, то (y,x) є Р-1, но тогда (x,y) є (Р-1)-1.
3. Функции. Инъекции, сюръекции, биекции. Понятие последовательности.
Отношение 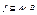 называется функцией или отображением из множества А в множество В, если
называется функцией или отображением из множества А в множество В, если 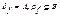 и из (x,y1) є f, (x,y2) є f следует y1=y2. Если вместо
и из (x,y1) є f, (x,y2) є f следует y1=y2. Если вместо 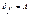 выполняется
выполняется 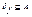 , то f называется частичной функцией. Функция f из А в В обозначается через
, то f называется частичной функцией. Функция f из А в В обозначается через 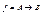 или
или 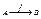 . Если (x,y) є f, то пишем y=f(x) или
. Если (x,y) є f, то пишем y=f(x) или 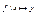 . Функция
. Функция 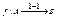 называется разнозначной инъективной (инъекцией) или 1-1 функцией если из условия, что
называется разнозначной инъективной (инъекцией) или 1-1 функцией если из условия, что 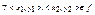 выполняется х1≠х2, следует y1≠y2. Функция
выполняется х1≠х2, следует y1≠y2. Функция 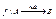 называется функцией из А на В или сюръекцией, если
называется функцией из А на В или сюръекцией, если 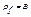 . Функция
. Функция 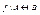 называется взаимно однозначным соответствием между множествами А и В или биекцией, если она инъективна и сюръективна одновременно.
называется взаимно однозначным соответствием между множествами А и В или биекцией, если она инъективна и сюръективна одновременно.
Биекция 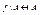 называется подстановкой.
называется подстановкой.
Утверждения:
1) Если 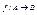 ,
, 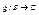 , то
, то 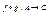
2) Если 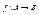 , то
, то 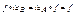
3) Если f и g - инъекции, то f•g – инъекция.
Доказательство: Предположим противное, т.е. найдутся элементы x1, x2, y такие, что х1≠х2, (x1,y) є f•g и (x2,y) є f•g, т.е. g(f(x1))=y=g(f(x2)). В силу разнозначности f имеем f(x1)≠f(x2). Отсюда в силу разнозначности g получаем g(f(x1))≠g(f(x2)), а это противоречит предположению.
4) Если f,g – сюръекции, то f•g – сюръекция
Доказательство: Нужно доказать, что для любого с существует а такое, что f•g(a)=c. Т.к. g – сюръекция, то существует b, для которого g(b)=c, а т.к. f – сюръекция, то для любого b существует а такое, что f(a)=b. Тогда f•g(a)=g(f(a))=c
5) Если f и g – биекции, то f•g – биекция
6) Если 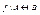 , то
, то 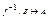
Функция 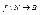 называется последовательностью. Её можно представить в виде f(0)=b0, f(1)=b1,…, f(n)=bn.
называется последовательностью. Её можно представить в виде f(0)=b0, f(1)=b1,…, f(n)=bn.
4. Множество натуральных чисел. Два подхода к определению множества натуральных чисел. Аксиомы Дедекинда-Пеано. Принцип математической индукции.
Два подхода к определению множества натуральных чисел:
1) Конструктивный.
Позволяет представить натуральные числа в виде объектов, построенных из пустого множества.
Положим по определению 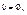
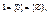
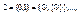
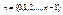 . Множества 0, 1, 2,… называются натуральными числами. Объединение этих чисел N={0, 1, 2,…, n,…} называется множеством натуральных чисел.
. Множества 0, 1, 2,… называются натуральными числами. Объединение этих чисел N={0, 1, 2,…, n,…} называется множеством натуральных чисел.
Замечание: АВ – множество всех функций из В в А. Если В=n={0,1,2…,n-1}, A=2={0,1}, то АВ=2n.
2) Аксиоматический подход.
Рассмотрим аксиоматику Дедекинда Пеано:
Пусть имеется некоторое множество N, в котором выбран элемент 0 и функция, которая элементу n из N ставит в соответствие элемент n’ из N, называемый непосредственно следующим (элемент n’ играет роль числа n+1).
Множество N называется множеством натуральных чисел, если система <N,0,’> удовлетворяет аксиомам:
- для любого m≠0 найдется n из N такой, что n’=m.
- для любых m,n из N, если m’=n’, то m=n.
- n’≠0 для любого n из N.
- на множестве N выполняется аксиома математической индукции.
Принцип (аксиома) математической индукции:
Для любого свойства Р (унарного отношения на множестве N), если Р выполняется на элементе 0 (т.е. 0 обладает свойством Р), и для любого n из N из выполнимости Р на элементе n следует выполнимость Р на элементе n’, то свойство Р выполняется на любом элементе n из N.
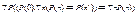 или
или 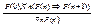 или
или 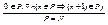
Иногда удается установить только выполнение Р(к) для некоторого к>0 и свойство Р(n)=>Р(n+1) для всех n≥к:
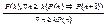
Принцип полной индукции:
Если для всякого n из N из предположения, что P(k) верно при любом натуральном k<n, следует, что P(k) верно также при k=n, то P(n) верно при любом натуральном n:
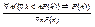
5. Понятие мощности множества. Сравнение мощностей. Теорема Кантора-Берштейна. Операции над кардинальными числами.
Множества А и В называются эквивалентными (А~В), если существует биекция f: А↔В.
Свойства отношения эквивалентности:
1) А~А (поскольку idA: А↔А);
2) если А~В, то В~А (т.к. из f: А↔В следует f-1: В↔А);
3) если А~В и В~С, то А~С (т.к. из f: А↔В, g: В↔С следует f•g: А↔С).
Мощностью множества А называется класс всех множеств, эквивалентных множеству А (|А|).
Эквивалентные множества А и В называются равномощными: |A|=|B|.
Если А~n для некоторого 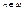 , т.е. А имеет ровно n элементов, то множество А называется конечным (|A|=n).
, т.е. А имеет ровно n элементов, то множество А называется конечным (|A|=n).
Множество, не являющееся конечным, называется бесконечным. Если А~ω, то множество А называется счетным: |A|=ω. Если А~2ω, то множество А называется континуальным или континуумом: |A|=2ω.
Мощности множеств также иногда называют кардинальными числами.
Сравнение мощностей:
Говорят, что мощность множества А не превосходит мощности множества В: |A|≤|B|, если А эквивалентно некоторому подмножеству множества В
Теорема Кантора-Бернштейна:
Если |A|≤|B| и |B|≤|A|, то |A|=|B|.
Доказательство: Пусть f: A→B, g: B→A – разнозначные отображения, А0=А, А1=g(B) и Аn+2=(f•g)(An). Индукцией по n легко показать, что 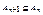 ,
, 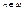 . Пусть
. Пусть 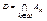 и
и 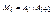 . Очевидно, что
. Очевидно, что 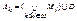 и
и 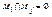 при i≠j. Т.к. f•g разнозначно отображает Mi на Мi+2 для любого
при i≠j. Т.к. f•g разнозначно отображает Mi на Мi+2 для любого 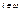 , то отображение h: А→А, определенное следующим образом:
, то отображение h: А→А, определенное следующим образом:
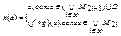
является разнозначным отображением А на 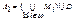 . Т.к. |B|=|A1|, |B|=|A|.
. Т.к. |B|=|A1|, |B|=|A|.
Следствие: Для любых множеств А и В выполняется только одно из соотношений: |A|=|A|, |A|<|B|, |B|<|A|.
Операции над кардинальными числами:
Пусть |A|=α, |B|=β. Тогда
1) 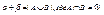 ;
;
2) 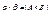 ;
;
3) 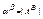 .
.
Для конечных кардинальных чисел справедливы следующие три правила, используемые в комбинаторике:
Правило суммы: Если |A|=m, |B|=n, то 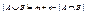 .
.
Правило произведения: Если |A|=m, |B|=n, то 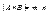 .
.
Правило степени: Если |A|=m, |B|=n, то |AB|=mn.
Некоторые свойства бесконечных кардиналов:
ω2~ω; ω~ 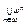 ; |Q|=ω; |P(U)|=2|U|; |U|<2|U|; если |A|>ω и |B|≤ω, то |A\B|=|A|; 2ω~10ω~ωω;
; |Q|=ω; |P(U)|=2|U|; |U|<2|U|; если |A|>ω и |B|≤ω, то |A\B|=|A|; 2ω~10ω~ωω;
6. Конечные, счетные, континуальные множества. Мощность булеана.
Если А~n для некоторого 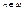 , т.е. А имеет ровно n элементов, то множество А называется конечным (|A|=n).
, т.е. А имеет ровно n элементов, то множество А называется конечным (|A|=n).
Множество, не являющееся конечным, называется бесконечным. Если А~ω, то множество А называется счетным: |A|=ω. Если А~2ω, то множество А называется континуальным или континуумом: |A|=2ω.
Мощности множеств также иногда называют кардинальными числами.
Мощность булеана:
|P(U)|=2|U| для любого множества U.
Доказательство:
Установим биекцию между Р(U) и 2А
Любому подмножеству А из U взаимно однозначно ставим в соответствие функцию 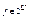 , для которой
, для которой
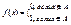
т.е. P(U)~2U. Заметим, что 2|U|=|2U|.
7. Матрицы бинарных отношений и их свойства. Специальные бинарные отношения.
Рассмотрим два конечных множества А={a1, a2,…, am}, B={b1, b2,…, bn} и бинарное отношение 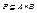 . Определим матрицу [P]=(pij) размера
. Определим матрицу [P]=(pij) размера 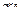 бинарного отношения Р по следующему правилу:
бинарного отношения Р по следующему правилу:
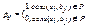
Полученная матрица содержит полную информацию о связях между элементами.
Основные свойства матриц бинарных отношений:
1) Если 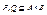 , [P]=(pij), [Q]=(qij), то
, [P]=(pij), [Q]=(qij), то 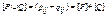 и
и 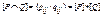 , где сложение осуществляется по правилам 0+0=0, 1+1=1+0=0+1=1, а умножение – обычным образом.
, где сложение осуществляется по правилам 0+0=0, 1+1=1+0=0+1=1, а умножение – обычным образом.
2) Если 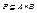 ,
, 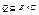 , то
, то 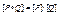 , где умножение матриц [P] и [Q] производится по обычному правилу умножения матриц, но произведение и сумма элементов по определенным в п.1 правилам.
, где умножение матриц [P] и [Q] производится по обычному правилу умножения матриц, но произведение и сумма элементов по определенным в п.1 правилам.
3) Матрица обратного отношения Р-1 равна транспонированной матрице отношения P: [P-1]=[P]T.
4) Если 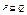 , [P]=(pij), [Q]=(qij), то pij≤qij.
, [P]=(pij), [Q]=(qij), то pij≤qij.
5) Матрица тождественного отношения idA единична: [idA]=E.
Специальные бинарные отношения:
Пусть Р – бинарное отношение на множестве А: 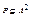
Отношение Р называется рефлексивным, если для всех 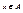 выполняется
выполняется 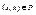 , т.е
, т.е 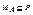 . Отношение Р называется симметричным, если для любых
. Отношение Р называется симметричным, если для любых 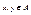 из
из 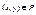 следует
следует 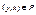 , т.е Р-1=Р, или [P]T=[P]. Отношение Р называется антисимметричным, если из
, т.е Р-1=Р, или [P]T=[P]. Отношение Р называется антисимметричным, если из 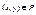 и
и 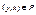 следует, что x=y, т.е
следует, что x=y, т.е 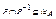 , или на языке матриц это означает, что в матрице
, или на языке матриц это означает, что в матрице 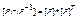 все элементы вне главной диагонали являются нулевыми. Отношение Р называется транзитивным, если из
все элементы вне главной диагонали являются нулевыми. Отношение Р называется транзитивным, если из 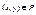 и
и 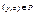 следует
следует 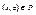 , т.е
, т.е 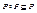
8. Отношения эквивалентности и разбиения. Фактор-множества. Матрица отношения эквивалентности.








