Радіус – вектор точки комплексної площини задається двома числами: -довжина (модуль) вектора, - кут між вектором і додатним направленням вісі Ох.

Дата: 2025-06-02; Просмотры: 8
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Якщо 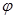- аргумент комплексного числа, то будь – яке число виду 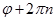, де 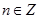, також є аргументом даного числа 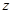. Вірно і зворотне твердження: якщо число 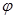є аргументом даного комплексного числа 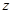, то воно можна подати у вигляді 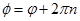, де 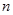- деяке ціле число. Обидва твердження очевидним чином випливають з властивостей періодичності тригонометричних функцій.

Два ненульових комплексних числа рівні тоді і тільки тоді, коли їх модулі рівні, а аргументи відрізняються на 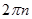, де .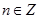

Наприклад:

1. Зобразіть на комплексній площині всі комплексні числа з аргументом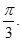

Усі комплексні числа з аргументом 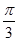зображуються точками комплексної площини, які є кінцями ненульових радіус – векторів, утворюють з додатним направленням вісі абсцис кут 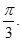Множиною таких точок являється промінь 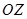, який утворює з додатним направленням вісі абсцис кут 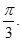Зауважимо, що при цьому мається на увазі промінь без початкової точки (мал.13).

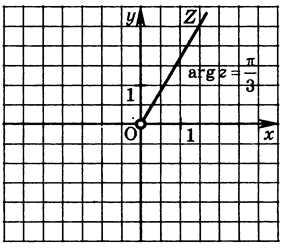
мал.13

2. Зобразіть на комплексній площині всі комплексні числа з аргументом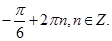

Всі комплексні числа з аргументом 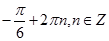зображуються точками комплексної площини, які є кінцями ненульових радіус – векторів, утворюють з додатним направленням вісі абсцис кут 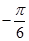. Множиною таких точок являється промінь 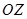, який утворює з додатним направленням вісі абсцис кут 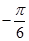. (мал.14)

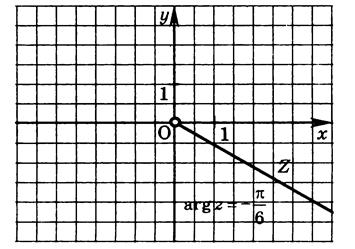
мал.14

3. Зобразіть на комплексній площині всі комплексні числа з аргументами 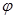такими, що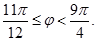

Всі комплексні числа з вказаними аргументами зображується точками комплексної площини, розташованими нижче промінів 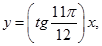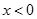і 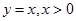. Цей кут без однієї з сторін та вершини (мал.15) .

мал.15

 

 

2.7.4. Тригонометрична форма комплексного числа.

Розглянемо на комплексній площині числа з модулем 1. Зображенням множини таких чисел являється коло з центром у початку координат та радіусом 1 (мал.16).

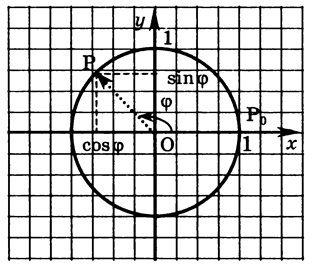
мал. 16

Нехай т. 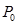- точка перетину кола з позитивним напрямом осі абсцис. Розглянемо точку Р кола, що зображує деякий комплексне число 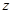. Точка Р є образом точки 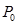при повороті з центром О на кут 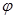, причому кут визначений з точністю до 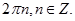Тоді абсциса х точки Р дорівнює 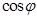, а ордината у дорівнює 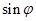. Тому комплексне число 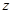задається формулою

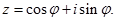
Зараз розглянемо довільне, відмінне від нуля, комплексне число 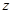з модулем 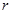, 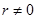. Тоді 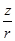- комплексне число, модуль якого дорівнює 1. Тому існує число 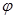таке, щ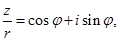о тобто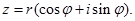

Запис 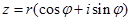при 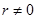називається тригонометричною формою комплексного числа .

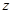Числа 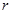і 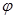називаються модулем і аргументом комплексного числа 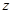. Для модуля та аргументу використовуються також позначення: 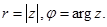Зазвичай вибирають значення 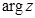, визначене нерівністю .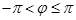