Модуль і аргумент комплексного числа
2.7.1. Полярні координати точки і її радіус-вектора
Кожному комплексному числу 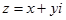 може бути поставлена у співвідношення точку
може бути поставлена у співвідношення точку 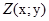 на комплексній площині, а кожній точці – радіус – вектор
на комплексній площині, а кожній точці – радіус – вектор  .
.
Точку Z можна задати також іншою парою чисел - полярними координатами: 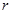 - відстань від початку координат (т.О) та кутом
- відстань від початку координат (т.О) та кутом 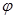 між променем OZ та додатним направленням вісі абсцис (мал. 8).
між променем OZ та додатним направленням вісі абсцис (мал. 8).
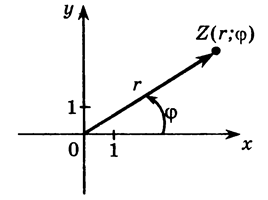
мал.8
Відповідно радіус – вектор точки Z задається тими ж числами, тобто 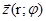 , де r – довжина (модуль) вектора,
, де r – довжина (модуль) вектора, 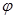 - кут між вектором і віссю ОХ.
- кут між вектором і віссю ОХ.
Для подальшого вивчення комплексних чисел нам необхідно згадати деякі властивості векторів:
1. Модуль (довжина) вектора  дорівнює
дорівнює 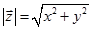 .
.
2. Кут між радіус-вектором і додатним напрямком осі абсцис - це кут повороту, при якому додатний напрям осі абсцис переходить в промінь, що задає напрямок даного вектора, при цьому початок променя є початок координат. Кут вважається додатним при повороті проти годинникової стрілки і від’ємним при повороті за годинниковою стрілкою.
Наприклад: В координатній площині задані вектори 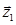 і
і 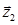 (мал. 9). Знайдіть їх модулі (довжини). Які кути вони утворюють з додатним направленням вісі абсцис?
(мал. 9). Знайдіть їх модулі (довжини). Які кути вони утворюють з додатним направленням вісі абсцис?
Так як 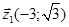 ,
, 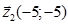 , то
, то 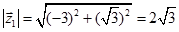 ,
, 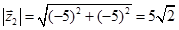 . Промінь
. Промінь 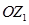 є образом променя Ох при повороті на кут, який дорівнює
є образом променя Ох при повороті на кут, який дорівнює 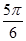 , а також при повороті на кут
, а також при повороті на кут 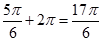 , або
, або 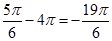 і так далі.
і так далі.
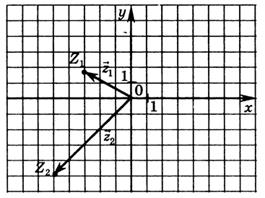
мал. 9
Тому вірне твердження, що вектор 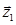 утворює з додатним направленням вісі абсцис кут
утворює з додатним направленням вісі абсцис кут 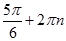 , де
, де 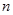 - будь – яке ціле число.
- будь – яке ціле число.
Аналогічним чином визначаємо, що вектор 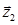 утворює з додатним направленням вісі абсцис кут
утворює з додатним направленням вісі абсцис кут 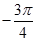 , або
, або 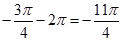 , або
, або 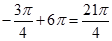 і так далі, тобто
і так далі, тобто 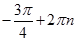 .
.
Відповідь: 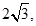
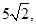
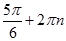 ,
, 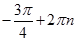 , де
, де 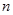 - будь – яке ціле число.
- будь – яке ціле число.
3. Нульовий вектор однозначно визначається модулем (довжиною), тобто кут між нульовим вектором і позитивний напрямом осі Ох не розглядається. Модуль нульового вектора дорівнює 0.
4. Нехай вектор 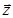 у прямокутній декартовій системі координат має координати х і у та утворює з додатним направленням вісі абсцис кут
у прямокутній декартовій системі координат має координати х і у та утворює з додатним направленням вісі абсцис кут 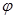 . Тоді
. Тоді
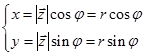 .
.
2.7.2. Модуль комплексного числа.
Модулем комплексного числа 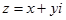 , де
, де 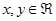 називається число
називається число 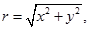 тобто
тобто 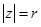 .
.
Властивості:
1. Якщо 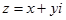 , де
, де 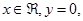 то
то 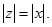
Доведення цієї властивості випливає з означення модуля комплексного числа.
Таким чином, поняття модуля комплексного числа є розвитком і узагальненням поняття модуля дійсного числа.
2. Модуль комплексного числа дорівнює модулю протилежного і спряженого цього числа чисел.
Доведення. Розглянемо комплексне число 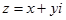 , де
, де 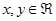 , а також протилежне
, а також протилежне 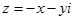 і спряжене
і спряжене 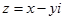 йому числа. Знайдемо їх модулі:
йому числа. Знайдемо їх модулі:
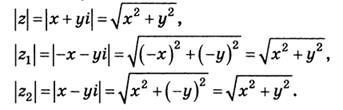
Властивість доведено.
3. Число 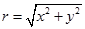 дорівнює модулю (довжині) вектора
дорівнює модулю (довжині) вектора  , тобто
, тобто 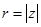 .
.
Наприклад:
1. Знайдіть 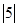 . Так як 5 – дійсне число, то з властивості 1 отримуємо
. Так як 5 – дійсне число, то з властивості 1 отримуємо 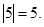
2. Знайдіть 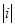 . Запишемо число і в алгебраїчній формі -
. Запишемо число і в алгебраїчній формі - 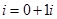 . Тоді з означення модуля комплексного числа, отримаємо:
. Тоді з означення модуля комплексного числа, отримаємо: 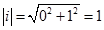 .
.
3. Знайдіть 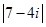 . Це число представлене в алгебраїчній формі. З означення модуля комплексного числа отримаємо:
. Це число представлене в алгебраїчній формі. З означення модуля комплексного числа отримаємо: 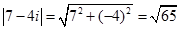 .
.
4. Покажіть на комплексній площині всі комплексні числа з модулем, рівним 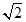 . Всі комплексні числа з модулем
. Всі комплексні числа з модулем 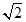 зображуються точками комплексної площини, які є кінцями радіус – векторів довжини
зображуються точками комплексної площини, які є кінцями радіус – векторів довжини 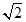 . Множиною таких точок є коло з центром у початку координат і радіусу
. Множиною таких точок є коло з центром у початку координат і радіусу 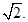 (мал.10)
(мал.10)
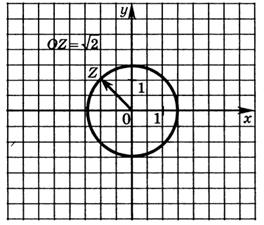
мал.10
Не порушуючи спільності міркувань, можна зробити наступний висновок.
Зображення множини комплексних чисел з модулем 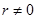 на комплексній площині є коло з центром на початку координат і радіусом
на комплексній площині є коло з центром на початку координат і радіусом 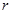 .
.
Доказ цього твердження полягає в послідовному застосуванні визначення модуля комплексного числа і визначення кола з центром на початку координат і радіусом 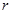 .
.
Наприклад:
1. Зобразіть на комплексній площині всі комплексні числа з модулем, меншим або рівним 2.
Всі комплексні числа з модулем, меншим або рівним 2, зображуються точками комплексної площині, які є кінцями радіус-векторів довжини, менше рівної 2. Безліч таких точок є коло з центром на початку координат і радіусом 2. (мал.11)
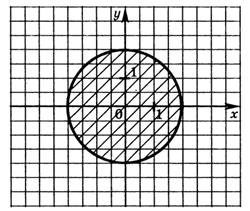
мал.11
2. Зобразіть на комплексній площині всі комплексні числа, що задовольняють умові: 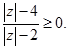
У цьому завданні розглядаються всі точки площини, крім точок, розташованих між концентричними колами і на меншому колі. Центри кіл - початок координат, радіуси рівні 2 і 4. (мал.12)
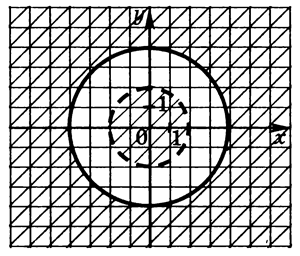
мал.12
2.7.3. Аргумент комплексного числа








