Ототожнюють пару вигляду з дійсним числом а. Неважко перевірити, що при такому ототожнені сумою і добутком пар і є пари , які за прийнятою умовою ототожнюються з числами і відповідно.

Дата: 2025-06-02; Просмотры: 6
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Аналогічно можна показати, що різниця і частка пар 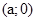і 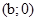- пари з нульовими другими елементами, тобто дійсні числа (для частки вважається, що ).

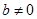Візьмемо тепер пару 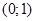і за правилом множення пар помножимо її саму на себе: 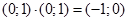(6) в результаті множення дістали пару 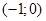, яка відповідає дійсному числу -1. Ввівши для пари 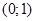спеціальне позначення 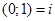, рівність (6) можна записати у вигляді 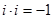або .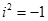

Проста перевірка показує, що будь – яку пару дійсних чисел 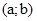можна записати у вигляді 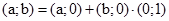або за прийнятою умовою про ототожнення множини всіх пар 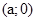і множини всіх дійсних чисел а і прийнятого позначення для пари 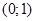, у вигляді 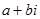. (7)

Введено операції додавання і множення впорядкованих пар дійсних чисел і показано, що будь – яке комплексне число можна записати у вигляді комбінації впорядкованих пар дійсних чисел (7).

2.6 Геометрична інтерпретація комплексних чисел.

2.6.1. Зображення комплексних чисел точками на площині

Розглянемо площину з введеною на ній прямокутною декартовою системою координат. Поставимо у відповідність кожному комплексному числу 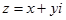(х і у – дійсні числа) у відповідність точку 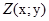координатної площини. Зауважимо, що встановлену відповідність між безліччю комплексних чисел і множиною точок координатної площини взаємно однозначно. Зауважимо також, що кожній точці 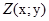координатної площини поставлений у відповідність радіус – вектор 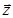(мал.3), координати якого співпадають з координатами точки Z.

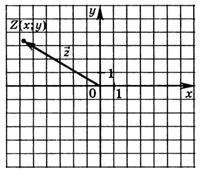
мал.3

Площина, на якій зображуються у вигляді точок комплексні числа, називається комплексною площиною.

Будь-якому дійсному числу відповідає точка 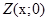а будь-якому суто уявному числу відповідає точка 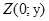. Тому всі дійсні числа зображуються точками осі абсцис, яка називається дійсною віссю, а все чисто уявні числа зображуються точками осі ординат, яка називається уявною віссю.

Наприклад:

1. Зобразіть на комплексній площині число .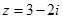

Цьому числу відповідає точка комплексної площини з координатами (3;-2), мал.4.

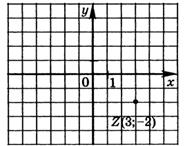
мал.4

2. Зобразіть на комплексній площині всі комплексні числа z, для яких вірно рівність .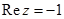

Це всі числа, які знаходяться на прямій, заданій наступною умовою х=-1, мал.5.

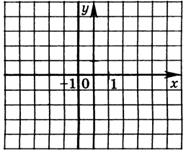
мал.5

2.6.2. Векторна інтерпретація операцій з комплексними числами

Проілюструємо операції додавання і віднімання комплексних чисел на комплексній площині.

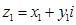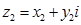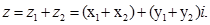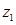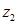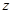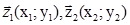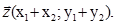Нехай дані комплексні числа і . Як відомо, їх сума теж комплексне число: Розглянемо відповідні числам , і радіус – вектори і Тоді 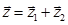. Нехай вектори 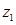, 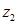не колінеарні. Так як вони мають спільний початок – початок координат т.О, то їх суму – вектор 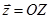можна побудувати за допомогою правила паралелограма (мал.6). Кінець цього вектору – точка 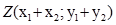- зображення комплексного числа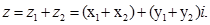

мал.6

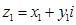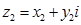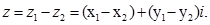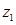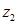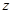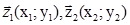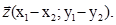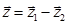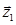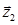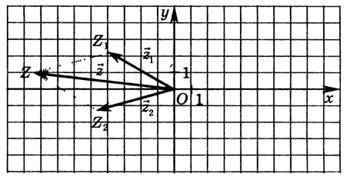
Розглянемо віднімання комплексних чисел і . Вона дорівнює комплексному числу Розглянемо відповідні числам , і радіус – вектори і Тоді . Вектори і мають спільний початок – початок координат т.О. Побудуємо їх різницю – вектор 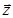- і відкладемо його від початку координат (мал. 7). Кінець цього вектора – точка Z – зображення числа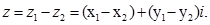

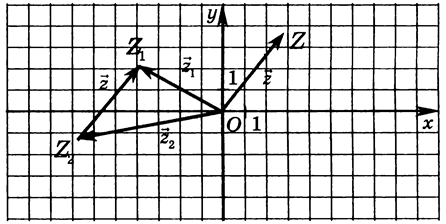
мал. 7

 

2.7. Тригонометрична форма комплексного числа.