Кожне комплексне число z може бути записане у вигляді: , де a і b – дійсні числа, а і – уявна одиниця. Ця форма запису комплексного числа називається алгебраїчною формою комплексного числа.
Дії над комплексними числами виконують за правилами дій над многочленами.
2.4 Дії над комплексними числами в алгебраїчній формі
2.4.1. Додавання комплексних чисел.
Сумою двох або кількох комплексних чисел називається комплексне число, дійсна частина якого дорівнює сумі дійсних частин доданків, а коефіцієнт уявної частини дорівнює сумі коефіцієнтів уявних частин доданків.
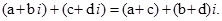
Наприклад:
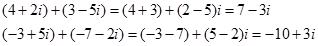
В області дійсних чисел є число "нуль", додавання якого до будь – якого іншого дійсного числа не змінює його.
В області комплексних чисел аналогічну роль відіграє число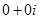 
. Справді, яким би не було комплексне число 
, 
.
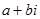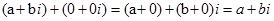З курсу математики ми знаємо, що сума двох дійсних чисел а і –а дорівнює нулю і вони називаються протилежними. Аналогічно з цим, комплексні числа 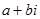і 
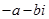також називаються протилежними: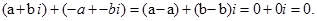 
Наприклад: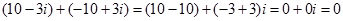 
.
Додавання комплексних чисел підлягає асоціативному і комутативному законам: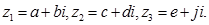 
1) комутативність: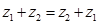 
.
.
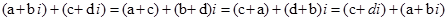2) асоціативність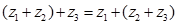 
.
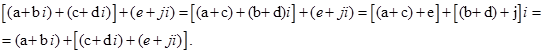
2.4.2. Віднімання комплексних чисел.
Різницею комплексних чисел є комплексне число, дійсна частина якого дорівнює різниці дійсних частин зменшуваного і від’ємника, а коефіцієнт уявної частини дорівнює різниці коефіцієнтів уявних частин зменшуваного і від’ємника.
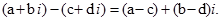
Наприклад: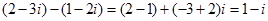 
.
Тобто від кожного комплексного числа можна відняти будь – яке інше комплексне число. Віднімання – це дія обернена додавання. Можливість такого віднімання і його однозначність потребує доведення.
Доведення.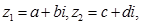 
а різницю цих чисел позначимо 
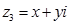. Доведемо, що для будь – яких комплексних чисел 
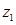і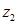 
різниця 
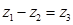визначена і притому однозначно.
Фактично нам потрібно довести, що існує, і при тому тільки єдине, комплексне число 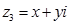, яке в сумі з 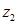дає :
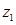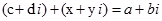(3)
За означенням суми комплексних чисел:
.
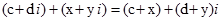Тому рівняння (3) можна переписати у вигляді
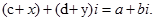
Два комплексних числа рівні тоді і тільки тоді, коли рівні їх дійсні частини і коефіцієнти при уявних частинах. Тому
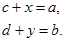
Ця система рівнянь завжди має розв’язок і притому єдиний:
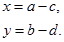
Таким чином, існує і при тому єдина пара дійсних чисел (х;у), що задовольняє рівняння (3). Отже, ми довели, що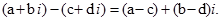
Щоб від одного комплексного числа відняти друге, досить це віднімання виконати окремо для дійсних частин цих чисел і коефіцієнтів при уявних частинах.
Наприклад:
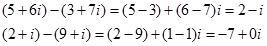
2.4.3. Множення комплексних чисел.
Два комплексних числа перемножуються за допомогою правил множення многочленів в алгебрі, слід тільки пам’ятати, що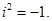 
Таким чином
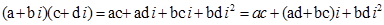
Але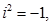 
тому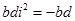 
і отже, 
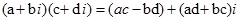(4)
Цю формулу (4) й покладено в основу означення добутку двох комплексних чисел.
Добутком двох комплексних чисел 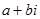і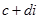 
називається таке комплексне число:
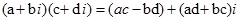
Наприклад:
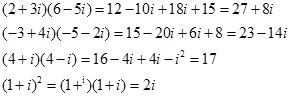
Висновок: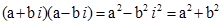 
.
Властивості множення комплексних чисел:
1) комутативність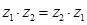 
2) асоціативність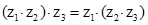 
3) 
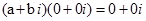
2.4.4. Ділення комплексних чисел.
Часткою від ділення комплексного числа 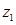на комплексне число 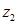називається таке число 
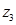, яке при множені на 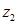дає .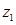
Доведемо, що частка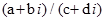 
визначена і при чому однозначно для всіх комплексних чисел 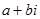і 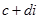, якщо 
.
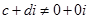Нам потрібно довести, що існує і при чому єдина пара дійсних чисел (х;у), що задовольняє рівнянню:
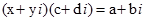. (5)
По правилу множення комплексних чисел:
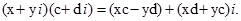
Тому рівняння (5) можна переписати у вигляді:
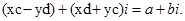
А з умови рівності двох комплексних чисел маємо:
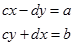
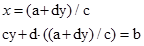
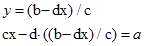
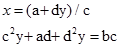
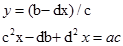
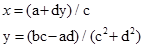
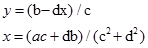
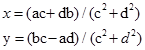
Таким чином,
.
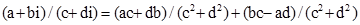Ця формула має зміст, якщо 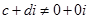. Отже ділення комплексних чисел можливе, якщо дільник не дорівнює нулю.
Легко перевірити, що правило ділення комплексних чисел можна одержати, якщо помножити ділене і дільник на число, спряжене з дільником:
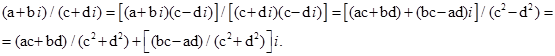
Наприклад:
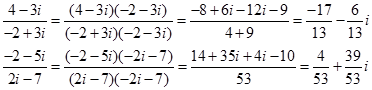
2.4.5. Піднесення до степеня уявної одиниці.
За означенням перша степінь числа і є саме число і.
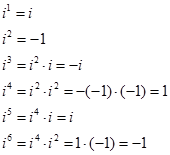
і т.д. Очевидно, що при будь-якому натуральному числі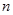 
:
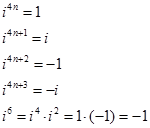
Отже, щоб піднести до степеня число і з натуральним показником 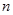, потрібно показник степеня розділити на 4 і піднести до степеня, показник якого дорівнює залишку від ділення.
Наприклад:
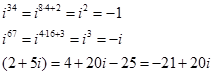
2.4.6. Квадратний корінь з комплексного числа.
Число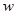 
називається квадратним коренем із комплексного числа 
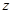, якщо його квадрат дорівнює : 
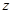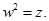
Квадратний корінь позначають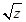 
.
Наприклад: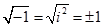 
.
Якщо раніше, розглядаючи квадратні рівняння з від’ємним дискримінантом, ми говорили, що такі рівняння не мають кореня, то тепер є. Квадратні рівняння з від’ємним дискримінантом мають комплексні корені. Ці корені дістаємо за відомими нам формулами.
Нехай, наприклад, дано рівняння:
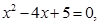
тоді
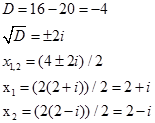
Отже, дане рівняння має корені:
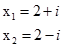
Ці корені є взаємно спряженими. Цікаво, що сума їх дорівнює -2, а добуток 5, так що справджується теорема Вієта.
Отже, ми можемо зробити висновок, що числа в області комплексних чисел також має місце теорема Вієта.
2.4.7. Властивості спряжених комплексних чисел.
Спряженими числами називаються два комплексні числа, які мають таку саму дійсну частину та протилежні за знаком уявні частини. Наприклад, спряженими є числа 3 + 4i та 3 − 4i. Число спряжене до числа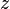 
позначається 
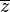. У загальному випадку, спряженим до числа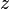 
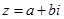є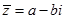 
Властивості:
· 
· 
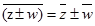
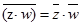
Наприклад:
.
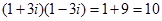2.5 Теорія комплексних чисел як упорядкованих пар дійсних чисел.
Розглянемо множину впорядкованих пар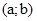 
, де a і b – дійсні числа. Дві пари 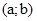і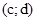 
вважаться рівними, якщо 
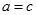і 
, і 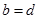записують 
.
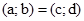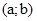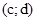Сумою пар і називають пару 
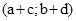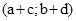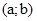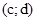. Кажуть, що пару дістали внаслідок додавання пар і і записують 
.
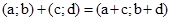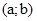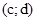Добутком пар і називають пару 
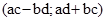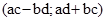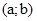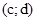. Кажуть, що пару дістали внаслідок множення пар і і записують 
.
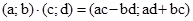Нульовою парою називають пару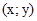 
, яка задовольняє умову 
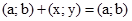, де 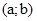- довільна пара. З означення операції додавання і рівності пар, випливає, що пара 
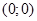- нульова.
Одиничною парою називають пару 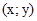, яка задовольняє умову 
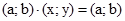, де 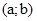- довільна пара. З означення операції множення і рівності пар, випливає, що пара 
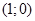- одинична.
У множині впорядкованих пар операції додавання і множення пар мають обернені операції – віднімання і ділення. Різницю і частку пар 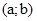і 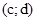обчислюють відповідно за формулами: 
,
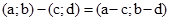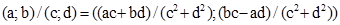(для частки вважається, що пара 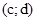- не нульова).