IV спосіб. Розглядається множина С формальних виразів виду , де символ і – просто деякий знак, а символи "+" і позначають відповідно алгебраїчні операції додавання і множення в множині С.
Означаються відношення рівності й алгебраїчні операції в С:
1) 
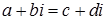тоді і тільки тоді, коли 
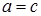і 
;
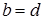2) 
;
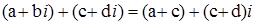3) 
.
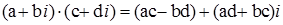Алгебраїчну систему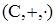 
називають системою комплексних чисел, а її елементи – комплексними числами. З властивостей 1-3 безпосередньою перевіркою отримують комутативний, асоціативний і дистрибутивний закони додавання і множення, а також те, що символ і є коренем незвідного над полем 
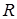рівняння 
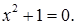Справді, з рівності 
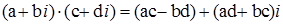при 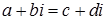маємо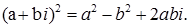 
Тоді при 
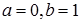отримуємо, що 
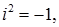тобто і є коренем рівняння 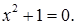Потім на основі введених операцій додавання і множення показується, що алгебраїчна система С утворює поле, яке є розширенням поля 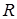дійсних чисел.
Позитивним моментом цього способу введення є строгий науковий підхід до викладу теорії, проте він може виявитися надто формальним і нецікавим для учнів середньої школи, що не сприятиме формуванню стійкого інтересу до математики.
Вищенаведені підходи відрізняються, але не суперечать один одному. В методичній літературі, зокрема підручниках, посібниках для середньої школи, найчастіше зустрічаються такі способи введення: перший та третій, які названі формальним та генетичним відповідно.
Нам ближче подання матеріалу теми генетично-геометричним способом, який ґрунтується на історичному розвитку поняття комплексного числа і на здоровому глузді та сприймається учнями природно і зрозуміло, не викликає у них психологічного протесту. Крім того, математичний розвиток старшокласників дає змогу розглядати внутрішні вимоги самої математики щодо виконуваності обернених операцій і універсальної розв’язності деяких найпростіших рівнянь як побічний вияв вимог практики. Введення операції не знаходить суперечностей і нагадує звичайні дії з дужками, що завжди подобається навіть несильним учням.
Саме цього способу я буду дотримуватися у своїй роботі.
2.2. Поняття розширення числа.
Одним з основних понять математики є поняття числа. Спочатку, в процесі рахування предметів, склалося поняття цілого додатного (натурального) числа – це поняття являється відображенням в свідомості людини кількісної сторони кінцевих зібрань (множин) предметів. Але вже найпростіші записи практики вчених, пов’язаних з вимірюваннями, привели до розширення поняття числа. Саме під впливом цих записів поступово склалося поняття додатного раціонального (дробового) числа і ірраціонального числа.
Але по іншому формувалося поняття від’ємного числа. Воно з’явилося під впливом внутрішніх потреб самої математики, в зв’язку з необхідністю зробити рівняння виду: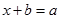 
розв’язуючим, навіть тоді, коли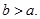 
Перші згадування про від’ємні числа і дії над ними зустрічаються у індійських математиків в VII ст. нашої ери. Їм також належить загальне теперішнє пояснення від’ємних і додатних чисел як арифметичних образів протилежно направлених величин. Саме це пояснення особливо сприяло тому, щоб поняття від’ємного числа стало рівноправним з поняттям додатного числа.
Кожне нове розширення поняття числа дозволяло розв’язувати такі задачі, які до цього були нерозв’язними. Так введення дробів дозволило виконати ділення двох чисел у всіх випадках, коли дільник не дорівнює нулю; введення від’ємних чисел дозволило проводити у всіх випадках віднімання; введення ірраціональних чисел дозволило виразити числом довжину відрізка, яка є несумірною з даною одиницею довжини.
Із курсу алгебри відомо, що числа цілі і дробові, як додатні так і від’ємні, і нуль називаються раціональними числами.
Нескінченні і періодичні десяткові дроби називаються ірраціональними числами.
Множина раціональних і ірраціональних чисел утворює множину дійсних чисел.
Поняття числа пройшло довгий шлях історичного розвитку. Однією з найпростіших числових множин є множина натуральних чисел: 1, 2, 3…. В ній завжди виконуються дві алгебраїчні дії: додавання і множення. Це означає, що, які б не були числа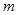 
і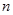 
їх сума 
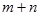і добуток 
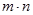неодмінно є натуральними числами. При чому справджуються такі п’ять законів:
1) комутативний закон додавання –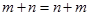 
;
2) асоціативний закон додавання –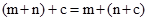 
;
3) комутативний закон множення –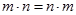 
;
4) асоціативний закон множення –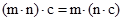 
;
5) дистрибутивний закон множення відносно додавання –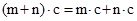 
.
Що ж до віднімання і ділення, то ці дві дії в множині натуральних чисел здійснюється не завжди. Так жодну з різниць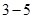 
або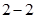 
, або жодну з часток 
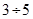і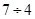 
ніяк не можна назвати натуральним числом.
Щоб віднімання завжди виконувалося, множину натуральних чисел потрібно було доповнити множину всіх від’ємних цілих чисел з нулем. В результаті такого доповнення або розширення ми переходимо до множини цілих чисел: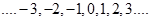 
.
Числова множина, в якій завжди здійснені операції додавання і множення, що підлягають вказаним вище п’ятьом законам, а також віднімання, називаються кільцем. Таким чином, множина всіх цілих чисел утворює кільце.
Розширивши множину всіх натуральних чисел, ми показали, з підручників, що дія віднімання може здійснюватися завжди. Але ділення так і залишилося невизначеним. Щоб усунути цю прогалину, треба розширити і множину цілих чисел. Зробити це можливо лише за допомогою приєднання множини звичайних дробів, тобто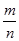 
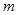, де і 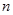- довільні цілі числа, і 
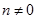. В результаті такого розширення ми отримуємо множину раціональних чисел. В цій множині завжди виконуються усі чотири дії: додавання, віднімання, множення і ділення.
Множина чисел, в якій завжди здійснені дії додавання і множення, що підлягають п’ятьом основним законам, а також дії віднімання і ділення (крім ділення на нуль) називається полем. Множина раціональних чисел є найпростішим числовим полем.
Зауважимо, що множина ірраціональних чисел не є полем. Будь – яка з чотирьох дій над ірраціональними числами може привести до раціонального числа. Наприклад: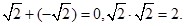 
У множині дійсних чисел завжди можливі всі шість алгебраїчних операцій: додавання, віднімання, множення, ділення, піднесення до степеня і добування кореня парного степеня з додатного числа.
2.3. Розширення множини дійсних чисел. Поняття комплексного числа.
Під час розв’язування деяких задач виникла потреба добувати квадратний корінь з від’ємних чисел. Зокрема, так було під час розв’язування квадратних рівнянь з від’ємним дискримінантом.
Наприклад: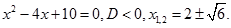 
Добування кореня парного степеня з від’ємного числа неможливо, якщо обмежуватися розгляданням тільки дійсних чисел. Серед дійсних чисел немає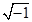 
. Коренем парного степеня з від’ємного числа являються особливі (не дійсні) числа.
Щоб виконувалась ця операція, необхідно розширити множину дійсних чисел приєднанням до неї нових чисел так, щоб множина утворила числове поле, в якому, крім перелічених вище дій, завжди можна було виконувати і добування коренів. Це питання було успішно розв’язане лише у ХІХ ст. При розширені множини дійсних чисел повинні виконуватися такі умови:
1) визначення нових чисел повинно опиратися на поняття дійсного числа, і нова множина повинна містити всі дійсні числа;
2) для нових чисел повинно виконуватися п’ять законів перших арифметичних дій;
3) в новій числовій множині повинно мати розв’язки рівняння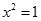 
, так як в цій множині повинна виконуватися дія, обернена до піднесення до степеня, вважаючи її розв’язком цього рівняння.
Домовившись 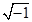позначити буквою і і називати уявною одиницею, тобто 
.
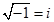Отже, за означенням і – число, квадрат якого дорівнює -1, тобто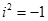 
.
Як бачимо, що нова множина, крім дійсних чисел, містить й число і.
Розв’яжемо квадратне рівняння: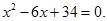 
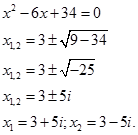
Кожен з найдених коренів представляє собою алгебраїчну суму дійсного і уявного доданків. Такі числа називаються комплексними числами.
Комплексним числом називається будь – яке число, яке має вигляд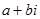 
, де a і b – дійсні числа, а і – уявна одиниця.
Оскільки в цій множині можливе множення, то вона містить і всі числа виду bi. Завжди можливе в цій множині і додавання, тому їй належать і всі числа виду 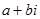. Число а прийнято називати дійсною частиною, вираз bi – уявною частиною комплексного числа 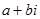. Число b називається коефіцієнтом при уявній частині. Комплексне число позначають буквою z.
Наприклад, для комплексного числа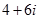 
дійсною частиною є 4, а уявною – вираз 6і, коефіцієнт при уявній частині дорівнює 6, для числа 
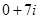дійсною частиною є число 0, а уявною – вираз 7і, коефіцієнт при уявній частині 7.
Із визначення комплексного числа випливає, що дійсні і уявні числа можна розглядати як окремі випадки комплексних чисел. Дійсно, в комплексному числі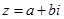 
коефіцієнт 
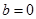то 
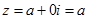. Комплексне число стає дійсним. Якщо ж 
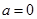, то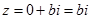 
, тобто комплексне число стає чисто уявним.
Поняття комплексного числа, яке ввійшло в математику ще з XVIII ст., на протязі довгого часу мало лише теоретичне значення і служило тільки потребам математики, утворюючи ряд незручностей при розв’язанні рівнянь. В науці доволі довго не було реальних явищ, які описувались би за допомогою комплексних чисел, і це призвело до того, що комплексні числа довго розглядалися як поняття, які не відповідають чому – не будь, що має місце в реальному світі. Звідси і походить термін "уявне число", тобто "реально не існуюче". Але в останній час цей погляд невірний.
Комплексне число використовується в багатьох науках: електротехніці, радіотехніці, аеродинаміці і т.д.
Із сказаного вище випливає, що комплексне число представляє корисне значення для нашої практичної діяльності розширення і узагальнення поняття числа, яке дозволяє описати важкі реальні явища, і тому являється поняттям таким же реальним, як і дійсне число.
Відносно комплексних чисел прийняті наступні властивості:
1. Два комплексних числа 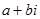і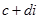 
називаються рівними тоді. І тільки тоді, коли їх дійсні і уявні частини рівні і рівні коефіцієнти при уявній одиниці, тобто 
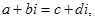якщо 
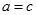і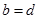 
.
З умови рівності комплексних чисел визначимо х і у у рівнянні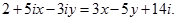 
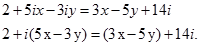
З умови рівності комплексних чисел випливає:
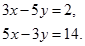
Розв’яжемо отриману систему з двох лінійних рівнянь з двома невідомими:
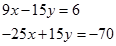
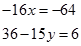
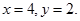
Перевірка: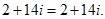 
2. З умови рівності комплексних чисел виходить, що комплексне число 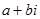дорівнює нулю тоді, і тільки тоді, коли його дійсна частина дорівнює нулю і коефіцієнт біля уявної частини дорівнює нулю, тобто 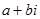, якщо 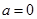і .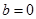
3. Модулем комплексного числа називається корінь квадратний із суми квадратів його дійсної частини і коефіцієнта біля уявної частини, тобто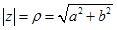 
. Модуль є величина додатна, тобто яка виражає арифметичне значення кореня.
Наприклад: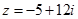 
, 
.
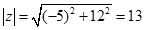4. Два комплексних числа 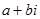і 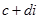, які відрізняються лише знаком коефіцієнта біля уявної частини, називаються спряженими.
Наприклад: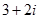 
і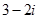 
- спряжені комплексні числа.
Комплексні корені квадратного рівняння завжди будуть спряженими числами.
Покажемо, що модулі двох спряжених чисел рівні між собою:
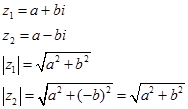
тобто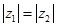 
.