Таким чином, кожному вектору осі відповідає дійсне число а, кожному вектору осі Оу – число . Тоді сумі векторів відповідає число (мал.2).
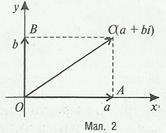
Отже, між точками координатної площини, упорядкованими парами ( a ; b ) дійсних чисел, які є координатами точок площини, векторами, початок яких збігається з початком координат, і виразами виду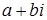 
можна встановити взаємно – однозначну відповідність.
Оскільки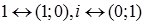 
і 
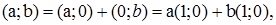то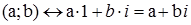 
.
Означення. Комплексним числом називається сума виду 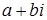, де a i b – дійсні числа, 1 і і – одиниці, взяті відповідно на осях Ох і Оу.
Далі означається рівність комплексних чисел. Оскільки дві координатної площини збігаються тоді і тільки тоді, коли їх відповідні координати рівні, то правомірним є таке означення рівності комплексних чисел.
Означення. Комплексне число 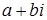дорівнює комплексному числу 
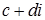тоді і тільки тоді, коли рівні відповідні їх дійсні й уявні частини, або, що те саме, коли вектори 
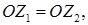де 
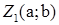і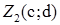 
. В іншому випадку комплексні числа називаються нерівними.
На користь цього методу можна навести такий аргумент: досить наочно проходять означення дій над комплексними числами, проте важко дається учням розуміння, як вектор на декартовій площині стає числом.
ІІІ спосіб. Поле комплексних чисел будують як просте алгебраїчне розширення поля дійсних чисел. Суть цього методу з наукового погляду полягає в такому. В алгебрі многочленів показують, що коли многочлен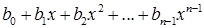 
степеня 
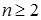незвідний над числовим полем Р (тобто не має коренів у цьому полі), а – число, корінь цього многочлена, то кожен елемент b поля Р(а), утвореного в результаті приєднання елемента а до поля Р, можна однозначно подати у вигляді:
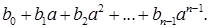(2)
Нехай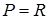 
і розглянемо многочлен 
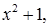який не має дійсних коренів. Позначимо число, щ є розв’язком рівняння 
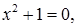через і і назвемо його числом нової природи. Отримаємо, що просте алгебраїчне розширення 
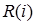і є полем комплексних чисел С. Справді, зі співвідношення (2) випливає, що кожен елемент з 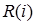матиме вигляд 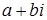, де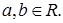 
Для учнів усі ці викладки теорії не наводяться. З метою універсальності розв’язності квадратних рівнянь множину дійсних чисел розширюють за допомогою приєднання до неї числа і, для якого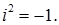 
За цих умов многочлени першого степеня відносно уявної одиниці і, тобто вирази виду 
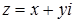, де х і у – дійсні числа, називають комплексними числами. Даний підхід носить назву генетичного, оскільки базується на історичному розширенні поняття числа і потребах науки, які приводять до цього розширення.
На користь цього методу говорить те,що він досить доступний учням, за його допомогою скорочується обсяг теоретичних викладок (без втрати відомостей) і уможливлює швидше перейти від теорії до практики обчислень і застосувань. Зв'язок нових чисел із реальною дійсністю є таким моментом, який у рамках шкільного курсу не може бути повністю висвітленим, тому при вивченні основ теорії комплексних чисел доцільно це враховувати і не допускати до того, щоб у свідомості учнів цей розділ запам’ятався як формально-логічна гра, що не має ніякого відношення до реального світу.