Показується, що алгебраїчна система утворює поле. Одиницею даного поля є пара (1;0), а нулем – пара (0;0). Далі розглядається рівність і отримують, що в полі С пара (0;1) є розв’язком рівняння
І.Вступ
Перед викладанням математики в школі крім загальних цілей навчання стоять ще свої специфічні цілі, що визначаються особливостями математичної науки. Одна з них – це формування і розвиток математичного мислення. Це впливає на виявлення і більш ефективний розвиток математичних здібностей школярів, підготовлює їх до творчої діяльності взагалі і в математиці з її багаточисленними застосуваннями вчасності.
Взагалі інтелектуальний розвиток дітей можна прискорити по трьом напрямкам: понятійна побудова мислення, мовний інтелект і внутрішній план дій.
Ґрунтовне засвоєння знань неможливо без цілеспрямованого розвитку мислення, яке є однією з основних задач загальної шкільної освіти.
Сучасне суспільство висуває випускникові школи досить високі вимоги. Ці вимоги стосуються і загальної культури випускника. У нашому випадку ми будемо говорити про математичну культуру, а ще точніше - про алгебраїчну.
З першого класу і до закінчення школи головним поняттям алгебри є поняття числа. Вивчення чисел йде послідовно - натуральні числа, дроби, цілі числа, ірраціональні, дійсні. На цьому загальноосвітня програма ставить крапку, залишаючи суттєву прогалину в знаннях учня, так як природним і логічно правильним є формування більш загального поняття - поняття комплексного числа. І на це є кілька причин.
По-перше, тема «Комплексні числа» традиційно входила в програми з математики старшої школи з поглибленим вивченням математики.
По-друге, ця тема включена в державний стандарт середньої (повної) освіти з математики (профільний рівень). Зокрема, наведемо цитату із стандарту (розділ «Числові та буквені вирази»): «Комплексні числа. Геометрична інтерпретація комплексних чисел. Дійсна і уявна частина, модуль і аргумент комплексного числа. Алгебраїчна і тригонометрична форма запису комплексних чисел. Арифметичні дії над комплексними числами в різних формах запису. Комплексно зв'язані числа. Зведення в натуральну ступінь (формула Муавра). Основна теорема алгебри ».
По-третє, комплексні числа важливі як область математики, в якій в повну силу працюють знання та вміння, отримані учнями при навчанні алгебри та тригонометрії.
І по-четверте, перехід від дійсних чисел до комплексних є завершальним кроком у всьому вивченні поняття числа в шкільному курсі математики.
До старших класів учні мають вже досить зрілим математичним розвитком: вони в змозі розуміти і поважати потреби самої математичної науки. Введення комплексних чисел являє собою чи не найяскравішу протягом шкільного курсу ілюстрацію діалектичного розвитку математичних понять, логічної простоти і завершеності. Поняття про число вибудовується в єдине струнке ціле. Коротко кажучи, безліч комплексних чисел виходить з безлічі дійсних чисел «додаванням» тільки одного нового числа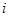 
, для якого 
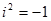, і всіх лінійних комбінацій виду 
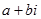з дійсними коефіцієнтами 
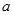и 
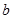. При «додаванні» єдиного кореня спеціального квадратного рівняння 
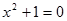ми перейдемо до чисел, в яких і будь-яке квадратне, і будь-яке кубічну, і будь-яке рівняння 
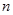-ого степеня має коріння.
Цілком природно також, що тільки в старших класах доречний повний, систематизуються погляд на розвиток поняття числа.
Метою даної роботи продемонструвати розвиток мислення старшокласників через формування нового поняття – поняття комплексного числа.
Задачі:
- дослідити особливості математичного мислення старшокласників;
- дослідити процес формування понять на матеріалі теми "Комплексні числа".
1.1 Історичні відомості
Людство завжди стикалося з проблемами нерозв’язності будь - яких завдань і шукало, іноді успішно, іноді ні, шляхи їх вирішення. Наприклад, у математиці, для того щоб будь-яке рівняння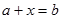 
мало корені, додатних чисел виявилося недостатньо і за два століття до н.е. китайськими математиками були введені від'ємні числа. Від’ємні числа допомогли описувати єдиним чином зміну величин.
Для розв'язання рівнянь виду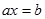 
було потрібно введення дробових чисел. Відомо, що за два тисячоліття до н.е. в Давньому Єгипті і Стародавньому Вавилоні вже застосовувалися дроби.
У VIII столітті нашої ери було встановлено, що квадратний корінь з додатного числа має два значення - додатне та від’ємне, і те, що з від’ємних чисел квадратні корені витягти не можна: ні, наприклад, такого числа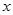 
, щоб виконувалася рівність 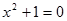. У XVI столітті в зв'язку з вивченням кубічних рівнянь виявилося необхідним навчитися витягувати квадратний корінь з від'ємних чисел. У 1545 році італійський математик Д. Кардано (1501 - 1576) запропонував ввести числа нової природи. Він показав, що система рівнянь 
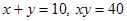, не має розв’язків в множині дійсних чисел, має розв’язок завжди, при 
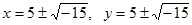, потрібно тільки умовитися діяти над такими виразами за правилами звичайної алгебри і вважати, що 
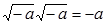. Кардано називав такі величини «чисто від’ємними» і навіть «софістическі від’ємними», вважаючи їх непотрібними, і прагнув не застосовувати їх, адже за допомогою таких чисел не можна виразити ні результат вимірювання якої-небудь величини, ні зміни цієї величини. Але вже в 1572 вийшла книга італійського алгебраїста Р. Бомбелли (бл. 1526 - 1572), в якій були встановлені перші правила арифметичних операцій над такими числами, аж до вилучення з них кубічних коренів. Далі комплексні числа застосовувалися в різних питаннях алгебри, але практичних застосувань поки не мали. Назва «уявні числа» ввів в 1637г. французький математик і філософ Рене Декарт.
Взагалі математики XVI в. і наступних поколінь аж до початку XIX століття ставилися до комплексних чисел з явною недовірою і упередженням. Вони вважали ці числа «уявними» (Рене Декарт), «неіснуючими», «вигаданими», «виниклими від надмірної мудрування» (Д. Кардано) [10]. Г. Лейбніц називав ці числа «витонченим і чудесним притулком божественного духу», а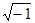 
, вважав символом потойбічного світу (і навіть заповідав накреслити його на своїй могилі).
Багато вчених цього періоду намагалися інтерпретувати комплексні числа на прямій лінії і застосовувати до таких понять, як наприклад, температура, час та ін., що не вимагає площинного зображення.
Пізніше, Л. Ейлер (1707 - 1783) ввів в математику символ 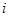, де .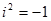
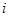( - це перша буква латинського слова imaginarius, що означає «уявний», «уявний»).
Також Л. Ейлером була виведена формула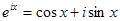 
, яка згодом була названа його ім'ям, хоча до Ейлера цією формулою володів англійський математик Р. Котес (1682 - 1716) [35]. Ця формула дозволила:
• довести періодичність експоненційної функції;
• вивести логарифми комплексних чисел.
Більш сувору теорію нової множини чисел, яка була названа комплексною, розвинув німецький вчений Карл Гаусс (1777 - 1855), який також дав їй геометричне тлумачення, що дозволило подолати багато труднощів в її розумінні. Хоча до Гаусса геометричне тлумачення зустрічається у датського землеміра К. весело (1745 - 1818) і французького математика Аргана (1768-1822). К. Гаусс в 1831 році дав глибоке обґрунтування комплексних чисел в математиці. Після того як з'явилося наочне геометричне зображення комплексних чисел за допомогою точок площини і векторів на площині (Гаусс в 1831 г, Вессель в 1799 г, Арган в 1806 г), стало можливим зводити до комплексних чисел і рівнянь для багатьох задач природознавства, особливо гідро - і аеродинаміки, електротехніки, теорії пружності і міцності, а також геодезії і картографії. З цього часу існування «уявних» або комплексних чисел стало загальновизнаним фактом і вони отримали таке ж реальний зміст, як і числа дійсні.
У XIX столітті О. Коші (1789-1857), Г. Ріман (1826-1866), і К. Вейерштрасс (1815-1897) на базі комплексних чисел створили нову математичну дисципліну - теорію функцій комплексного змінного, яка відіграє важливу роль у сучасній математики.
З розвитком науки і техніки ставало все більш зрозумілим, що без комплексних чисел не можна обійтися в багатьох практичних справах. Широке застосування знайшли комплексні числа в електротехніці, гідродинаміці, картографії, в теорії літака і багатьох інших галузях. Зараз важко вказати область фізики, механіки, технічних дисциплін, де не застосовувалися б комплексні числа.
ІІ. Теоретична частина
2.1 Особливості формування і засвоєння основних понять теорії комплексних чисел.
На сучасному етапі комплексні числа внесено до програми поглибленого вивчення математики учнями загальноосвітніх та програм курсів за вибором для профільного чи академічного рівнів. Тому постає питання про розгляд способів введення поняття комплексного числа та вибору з них найбільш доцільного.
Формування поняття числа – одне з найважливіших завдань методики і один з методологічних аспектів філософських проблем математики: розвитку математичного пізнання. На прикладі формування поняття числа можна простежити процес виникнення і розвитку наукових понять.
У процесі розвитку математичні знання старшокласників поповнюються такими новими поняттями, абстрактний характер яких значно підсилюється. При засвоєнні цих понять чуттєво-предметна діяльність учнів звужується до мінімуму, але при цьому однозначно зростає роль інтелектуальної діяльності.
Методика вивчення цих понять має базуватися на використанні історичних і конкретно-практичних даних про їх введення, а це дає змогу обґрунтувати питання зв’язку математики з практикою, що й показується наприкінці вивчення конкретної теми. При цьому потрібно звернути особливу увагу на розкриття логіко-математичних зв’язків нових абстракцій з уже відомими учням математичними поняттями.
Під час формування основних понять теорії комплексних чисел, які належать до понять високого рівня абстракції, важливі такі моменти:
- цілеспрямоване формування головного образу певного поняття – образу, який має міцну опору в досвіді учня;
- варіативність образу, яка включає: зміну "первинного образу" в процесі розкриття змісту поняття; використання різних форм представлення нового математичного поняття;
- тісний взаємозв’язок з раніше вивченим за рахунок того, що первинний образ будується на попередньому знанні і його використанні в новій ситуації;
- схематизація: використання різних форм подання математичних фактів створює можливості для виявлення зв’язків усередині цієї теми, зв’язків нових знань з попередніми; результатом виявлення цих зв’язків і структурування вивченого стає побудова схеми, що відображає суть поняття і фіксує її за допомогою знакових засобів. Ці засоби виступають у ролі опорного сигналу, який допомагає учням у подальшому "розгорнути" вивчене поняття, дію в повному обсязі;
- розкриття можливостей застосування поняття під час розв’язування прикладних задач із міжпредметними та внутрішньо предметними зв’язками.
Основні поняття теорії комплексних чисел:
комплексне число, модуль комплексного числа, аргумент комплексного числа, алгебраїчна форма комплексного числа, тригонометрична форма комплексного числа, протилежні комплексні числа тощо.
Як відомо, багатьом основним поняттям теорії комплексних чисел взаємно – однозначно відповідає визначений геометричний образ. Це й історично стало поштовхом до виникнення різних підходів до побудови теорії комплексних чисел. Аналіз наукової і методичної літератури допоміг виявити існування різних підходів до введення поняття комплексного числа та виділити основні з них.
І спосіб . Комплексне число z вводиться як упорядкована пара ( a ; b ) дійсних чисел. Множину таких упорядкованих пар позначають символом С. На цій множині визначається відношення рівності і дві бінарні алгебраїчні операції – додавання і множення – таким чином: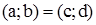 
тоді і тільки тоді, коли 
; 
; 
.
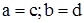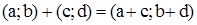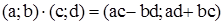Показується, що алгебраїчна система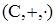 
утворює поле. Одиницею даного поля є пара (1;0), а нулем – пара (0;0). Далі розглядається рівність 
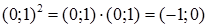і отримують, що в полі С пара (0;1) є розв’язком рівняння
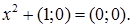(1)
Позначивши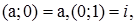 
отримують алгебраїчну форму запису комплексного числа ( a ; b ): 
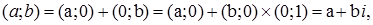при чому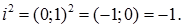 
Потім доводиться, що поле С є мінімальним полем, яке містить поле дійсних чисел і в якому має розв’язок рівняння (1), а також, що таке поле єдине з точністю до ізоморфізму.
Далі пояснюється, що дії над комплексними числами в алгебраїчній формі виконується, як над многочленами, і чому саме вибрано на початку саме такі означення дій над комплексними числами.
Такий спосіб побудови комплексних чисел є певною мірою формальним та вказує на "тонкі" моменти теоретичного характеру.
ІІ спосіб . Встановлюються взаємно-однозначні відповідності між дійсними числами, точками координатної прямої і векторами, початок яких збігається з початком координат. При цьому додатному числу х ставлять у відповідність вектор, довжина якого х, а напрям збігається з напрямом координатної прямої, від’ємному числу х – вектор, модуль якого дорівнює х, а напрям – протилежний до напряму координатної прямої, тобто кут між напрямом вектора і напрямом координатної прямої дорівнює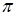 
.(мал.1) Нулю відповідає нульовий вектор, модуль якого дорівнює нулю і якому не приписують ніякого напряму.
При такій (векторній) інтерпретації дійсних чисел дії додавання і віднімання між ними можна інтерпретувати як паралельне перенесення. Так, перетворення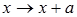 
зсуває кожну точку х прямої на а одиниць право, якщо а додатне, і на а одиниць вліво, якщо а від’ємне. Таким чином, додаванню дійсних чисел відповідає додавання векторів і навпаки, тобто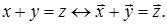 
Множення і ділення дійсних чисел подається як перетворення гомотетії відносно початку координат. При перетворенні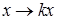 
, якщо 
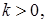то маємо або розтяг вектора 
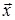при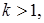 
або стиск його при 
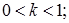і якщо 
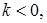то відповідно розтяг або стиск із зміною напряму (центральну симетрію відносно точки 0). При такій інтерпретації множення на число задає відображення множини дійсних чисел на себе.
Позначають один із коренів рівняння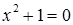 
через і, тоді за означенням кореня рівняння 
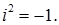Відтак множення дійсного числа на і2, яке є рівносильним множенню на -1, можна тлумачити як двократне множення на і. Інакше кажучи, двократне множення дійсного числа на і означає поворот навколо початку координат на кут 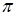. Тому, правомірно вважати, що множення на і означає поворот навколо початку координат на кут 
.
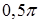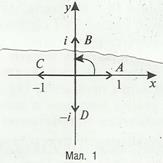
Застосування множення на і одиничного вектора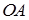 
дає вектор 
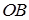, перпендикулярний до нього: 
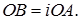Проведемо нову вісь координат 
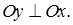Тоді вектору 
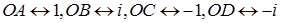(мал.1). Аналогічні міркування, коли довжина вектора відмінна від одиничної.