Основная теорема арифметики.

Дата: 2025-06-02; Просмотры: 8

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Теорема 9. Составное натуральное число единственным образом с точностью до порядка следования разлагается в произведение простых чисел.

Замечание. Эта теорема позволяет представлять натуральное число в виде произведения степеней различных простых чисел и использовать единственность этого разложения.

Определение. Разложение числа 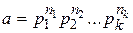, где 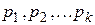- различные простые числа, называется каноническим разложением или каноническим видом числа а.

Вычисление НОК и НОД по каноническому виду чисел.

По основной теореме арифметики любое натуральное число можно представить в виде произведения степеней различных простых чисел. Но, т.к. по определению любое натуральное число в нулевой степени равно единице, то мы можем при необходимости несколько менять канонический вид натурального числа, добавляя некоторые простые множители в нулевой степени. Например, 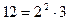, но по сути ничего не изменится, если записать 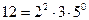.Таким образом, рассматривая одновременно несколько натуральных чисел, мы можем полагать, что в их канонические разложения входят одни и те же простые числа но некоторые из них возможно находятся в нулевой степени, т.е показатели простых чисел в канонических разложениях будем считать целыми неотрицательными числами.

Теорема 10. Пусть числа а и b представлены в каноническом виде: 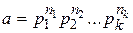, 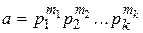. Тогда НОД(а; b)= 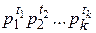и НОК(а; b)= 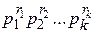, где ; .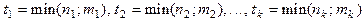

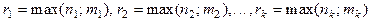Замечание. Данную теорему можно распространить для любого количества чисел.

Пример. Найдем НОД и НОК для чисел 108, 300 и 840.

Для начала представим данные числа в виде из канонических разложений: 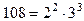, , 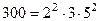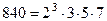. В канонических разложения этих чисел встречаются простые множители 2, 3, 5, 7 В различных степенях. При этом их наименьшие степени в данных разложениях: 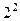- у чисел 108 и 300, 3 - у чисел 300 и 840, 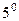- у числа 108, 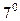- у чисел 108 и 300. Поэтому НОД(108;300;840)= 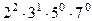=12.

Аналогично, наибольшие степени этих же простых чисел в данных канонических разложениях: 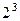- у числа 840, 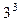- у числа 108, 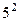- у числа 300, 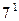- у числа 840. Поэтому НОК(108;300;840)= 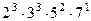=37800.

Алгоритм Евклида.

Отыскание НОД и НОК методом разложения на простые множители иногда бывает трудной задачей, поскольку сам процесс разложения на множители часто бывает затруднителен. Например, разложение на простые множители числа 1521 потребует многих проб на делимость, т.к. 1521=39², т.е. наименьший простой делитель достаточно велик.

В таких случаях для нахождения НОД удобно применять способ, предложенный греческим математиком Евклидом (III в. до н.э.). Данный метод получил название “алгоритм Евклида”.

Суть этого метода заключается в последовательном делении с остатком. Пусть даны два числа а и b и пусть, для определенности, а> b. Разделим с остатком а на b, по определению деления с остатком получим:

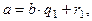где .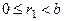

Затем разделим число b на получившийся остаток :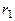

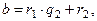где .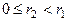

Теперь разделим 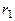на вновь получившийся остаток 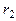и т.д. :

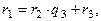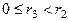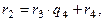где ,

где ,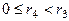

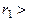
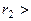
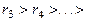
Такой процесс деления будем продолжать до тех пор, пока на каком-то шаге не получим остаток равный 0. Этот факт следует из того, что каждый следующий остаток, получаемый в процессе деления меньше предыдущего: 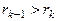... И т.к. все остатки являются целыми неотрицательными числами, то через конечное число делений один из остатков будет равен 0, пусть таким остатком будет :

. . . . . .

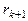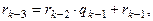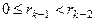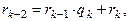где ,

где ,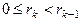

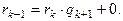
Тогда последний из остатков отличный от 0 - 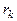и будет наибольшим общим делителем чисел а и b.

Замечание. В случае, когда уже первый остаток 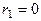, число а делится на b, поэтому НОД(а; b)=b.

Пример. Найдем НОД(30107;5083). Для удобства запись будем вести следующим образом:

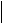
		30107	5083
		25415	5
	5083	4692
	4692	1
4692	391
391 .	12
782
782
0

Отсюда НОД(30107;5083) = 391.

Некоторые свойства НОД и НОК.

Теорема 11. Произведение НОД(а; b) на НОК(а; b) равно произведению самих чисел а и b.

Замечание. Данная теорема позволяет в случае, когда найден НОД(а; b), например, по алгоритму Евклида, найти НОК(а; b).

Следствие. Наименьшее общее кратное взаимно простых чисел равно их произведению.

Теорема 12. Пусть НОД(а; b)= D, а НОК(а; b)=М, тогда НОД(а; b;с)= НОД( D;с) и НОК(а; b;с)= НОК(М;с).

Замечание 1. Данная теорема позволяет при отыскании НОД и НОК нескольких чисел производить это последовательно, заменяя некоторую пару чисел их НОД или НОК соответственно.

Замечание 2. Данную теорему можно распространить для любого количества чисел.