Наименьшее общее кратное (НОК).
Если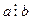 
, то говорят, что a кратно b.
Определение. Если число m кратно каждому из чисел а1, а2, ... а k, то т называют общим кратным этих чисел.
По свойству транзитивности отношения делимости числа вида 2т, 3т, ... nт также являются общими кратными для чисел а1, а2, ... а k,.
Среди натуральных общих кратных должно существовать наименьшее натуральное число (по принципу наименьшего числа), которое называется наименьшим общим кратным.
Обозначается: НОК(а1, а2, ... а k)=т.
Замечание. Число 0 является общим кратным для любых чисел. Мы будем рассматривать только натуральные общие кратные чисел.
Наибольший общий делитель.
Определение. Если каждое из чисел а1, а2, ... а k, делится на число d, то d называют общим делителем этих чисел..
Очевидно, что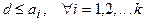 
. Тогда среди чисел от 1 до наименьшего из чисел а1, а2, ... а k можно выбрать наибольший общий делитель данных чисел.
Обозначается: НОД(а1, а2, ... а k)=d.
Определение. Если НОД(а1, а2, ... а k)=1, то числа а1, а2, ... а k называют взаимно простыми.
Признаки делимости на составные числа.
Теорема 8. Пусть число т разложено в произведение взаимно простых чисел а и b: т=а b, где НОД(а; b)=1. Некоторое число S тогда и только тогда делится на т, когда оно делится и на а и на b.
Замечание1. Данная теорема позволяет расширить перечень уже известных признаков делимости, включив признаки делимости на некоторые составные числа, при условии, что их можно разложить на произведение взаимно простых чисел.
Пример. Число 18 можно представить как произведение взаимно простых чисел 2 и 9, поэтому можно сформулировать признак делимости на 18 следующим образом: некоторое число делится на 18 тогда и только тогда, когда оно одновременно делится на 2 и на 9.
Замечание2. Данную теорему можно применять многократно.
Пример. Число 42 можно представить как произведение взаимно простых чисел 7 и 6, но в свою очередь число 6 можно представить как произведение взаимно простых чисел 2 и 3, т.о.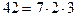 
. Признак делимости на 42 можно сформулировать следующим образом: некоторое число делится на 42 тогда и только тогда, когда оно одновременно делится на 7, на 2 и на 3.