Делимость целых неотрицательных чисел.
Определение. Будем говорить, что число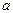 
делится на число 
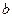,если существует целое неотрицательное число 
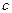, что 
.
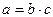(Говорят, что а кратно b, а b называют делителем числа а.)
Обозначение: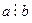 
.
ПРИЗНАКИ ДЕЛИМОСТИ.
Признак делимости - это предложение, сводящее вопрос о делимости данного натурального числа к вопросу о делимости меньшего натурального числа.
Признак делимости суммы.
Теорема 1.(Необходимый и достаточный признак.) Сумма двух или нескольких слагаемых делится на данное число в том и только том случае, когда сумма остатков получаемых при делении слагаемых на данное число кратна этому числу.
Следствие 1. (Достаточный признак делимости суммы.) Если каждое слагаемое делится на некоторое число, то и сумма делится на это число.
Следствие 2. (Признак неделимости суммы.) Если только одно слагаемое не делится на некоторое число, а все остальные делятся, то сумма всех слагаемых на это число не разделится.
Признак делимости разности.
Теорема 2. (Необходимый и достаточный признак.) Разность двух чисел делится на данное число в том и только в том случае, когда равны остатки получаемые при делении на это число уменьшаемого и вычитаемого.
Следствие.(Достаточный признак.) Если уменьшаемое и вычитаемое делятся на некоторое число, то и разность разделится на это число.
Признак делимости произведения.
Теорема 3. (Необходимый и достаточный признак.) Произведение делится на данное число в том и только том случае, когда произведение остатков, получаемых при делении сомножителей на данное число, кратно этому числу.
Следствие .(Достаточный признак.) Если хотя бы один из множителей делится на данное число, то и все произведение делится на это число.
Признаки делимости чисел, заданных в позиционных системах.
Признак делимости на 2.Число тогда и только тогда делится на 2, когда его десятичная запись кончается одной из цифр 0, 2, 4, 6, 8.
Признак делимости на 5. Число тогда и только тогда делится на 5, когда его десятичная запись кончается одной из цифр 0 или 5.
Признак делимости на 4. Число тогда и только тогда делится на 4, когда его две последние цифры образуют число, делящееся на 4.
Признак делимости на 25. Число тогда и только тогда делится на 25, когда его две последние цифры образуют число, делящееся на 25 (т.е. оно оканчивается двумя нулями или на конце его стоят числа 25, 50, 75).
(Доказательство аналогично доказательству признака делимости на 4.)
Признак делимости на 9. Число тогда и только тогда делится на 9, когда сумма цифр его десятичной записи делится на 9.
Признак делимости на 3. Число тогда и только тогда делится на 3, когда сумма цифр его десятичной записи делится на 3.
Признак делимости на 11. Число тогда и только тогда делится на 11, когда разность между суммой его цифр, стоящих на четных местах и суммой его цифр, стоящих на нечетных местах делится на 11 (обычно из большего числа вычитают меньшее).
3. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА.
Определение. Натуральное число а, отличное от 1 называется простым, если оно делится на себя и на 1. Натуральное число а называется составным, если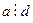 
, где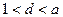 
.
Таким образом, по числу различных натуральных делителей все множество целых неотрицательных чисел разбивается на четыре непересекающихся подмножества:
1. Число 1 имеет только один натуральный делитель.
2. Простые числа имеют точно по два натуральных делителя.
3. Составные числа имеют не менее трех различных натуральных делителей.
4. Число 0 имеет бесконечно много натуральных делителей.
Решето Эратосфена.
Мысль о создании таблицы простых чисел возникла еще у математиков древней Греции. Простой метод создания таблицы простых чисел, содержащихся на отрезке натуральной последовательности от 1 до n, нашел греческий математик и астроном Эратосфен (III в. до н.э.)
Как правило, на практике при необходимости определения составным или простым является данное число, составление таблицы простых чисел не является целесообразным (особенно, если это число достаточно велико). Для такой цели используют способ, основанный на следующем утверждении:
Теорема 6. Наименьший простой делитель составного числа а не превосходит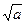 
.
Из данной теоремы следует, что если число а не делится ни на одно простое число, не превосходящее 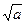, то у него совсем нет простых делителей, меньших самого числа, т.е. данное число простое.
НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ.