Глава 4. Результаты оптимизации
4.1. Описание программы
Для реализации поставленной задачи была написана программа с использованием языка программирования СИ.
Данная программа проводит оптимизацию диска с помощью МКЭ и МКР. Способ расчета можно выбрать до начала работы программы. На вход подаются все данные о материале диска, такие как модуль упругости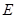 
, коэффициент Пуассона 
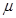, плотность 
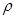и температурный коэффициент 
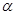; так же данные о размерах диска – внешний и внутренний радиусы и толщина; и, наконец, данные о нагрузке на диск – приложенная распределенная сила, температурный градиент и моменты. Так же в программе можно задать ограничение на минимальную и максимальную толщину диска.
Перед началом работы программы нужно задать значения управляющих параметров:
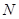- количество узлов (точек, находящихся на равном расстоянии по всей длине диска);
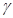и 
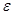- отвечают за норму изменения толщины на каждой итерации;
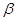- отвечает за сглаживание функции толщины диска.
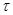- отвечает за норму отклонения получившегося напряжения в точке от допустимого напряжения.
Все эти пять параметров сильно влияют на скорость и характер сходимости алгоритма.
Алгоритм можно запустить с двумя способами останова:
1. До полной его сходимости с заданной точностью.
В этом случае количество итераций определяется программой автоматически и на выходе получается форма диска, которая в большей или меньшей степени удовлетворяет всем заданным параметрам.
2. Задать на входе количество итераций.
В этом случае программа проведет нужное количество итераций и на выходе получается форма диска, которая необязательно будет удовлетворять всем ограничениям. При таком запуске удобно смотреть текущее состояние диска и скорость сходимости. Так же, при желании можно посмотреть результаты работы алгоритма после того как оптимальная форма уже найдена (для этого необходимо задать количество итерации больше, чем необходимо для сходимости алгоритма).
После завершения работы программы можно посмотреть результаты расчетов всех требуемых параметров, например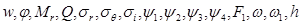 
и их графики в зависимости от 
.
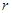При реализации алгоритма предполагалось, что расчет диска будет вестись только методом конечных элементов, но, после проведения первых расчетов стала ясна непригодность этого подхода. В результатах оптимизации были явно выражены биения почти всех ключевых функций. Вследствие этого пришлось отдать предпочтение менее точному на малом количестве узлов методу конечных разностей. Но увеличение количества узлов в данном случае не привело к значительному увеличению времени расчета программой, так как время одной итерации МКР значительно меньше времени одной итерации МКЭ.
4.2. Примеры расчетов оптимальных дисков
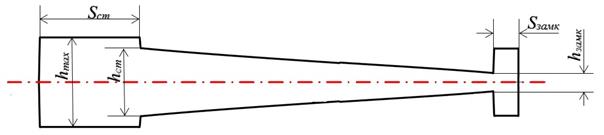
Приведем параметры диска, учитываемые при решении задачи (см. рис. 4.1):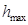 
- максимальная толщина диска, 
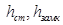- толщины ступицы и замкового соединения, 
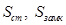- высоты ступицы и замкового соединения.
|
| Рис. 4.1. Параметризация диска |
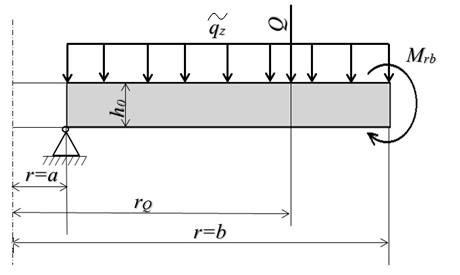
Для всех приведенных ниже примеров в качестве исходной конфигурации примем диск постоянной толщины, к которому приложены различные нагрузки (см. рис. 4.2). Варьируя начальную толщину диска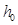 
можно получить оптимальные диски при разных нагрузках.
|
| Рис. 4.2. Постановка задачи весовой оптимизации пластинки |
|
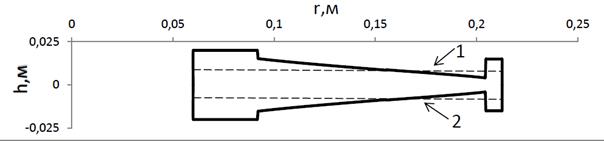
Рис. 4.3. Оптимальная форма диска
(пунктирная линия - толщина начального проекта, сплошная – оптимальный диск)
|
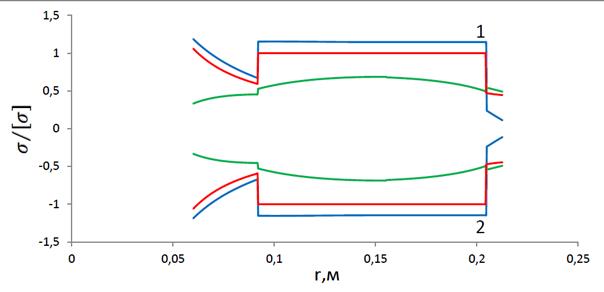
Пример 1. Диск нагружен поперечной распределенной нагрузкой, с ограничением на толщину ступицы (0.04м) и с замковым соединением толщиной 0.015м (cм. рис. 4.1 и 4.2). Диск изготовлен из материала с модулем Юнга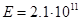 
Па, коэффициентом Пуассона 
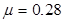, имеет плотность 
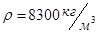, внутренний радиус 
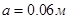, внешний радиус 
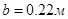. Толщина проекта диска на первой итерации постоянна и равна 
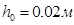, поперечная нагрузка распределена по всему радиусу равномерно 
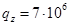Па, допустимые напряжения 
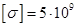Па (см. рис. 4.3).
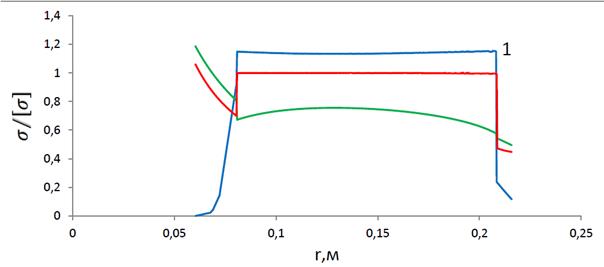
В силу симметрии диска напряжения на поверхностях 1 и 2 равны по модулю и противоположны по знаку, поэтому в следующих двух примерах приведем только напряжения на поверхности 1 (напряжения на поверхности 2 получаются их зеркальным отображением относительно нуля).
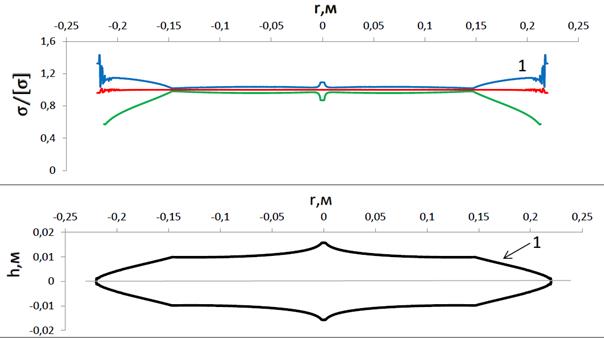
Пример 2. Диск нагружен поперечной распределенной нагрузкой, изгибающим моментом на внешнем радиусе и температурными напряжениями, параметры диска совпадают с параметрами из Примера 1 (см. рис. 4.4). К ним добавляется температурная нагрузка (температура изменяется линейно, на внутреннем радиусе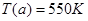 
, на внешнем 
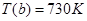) и к внешнему радиусу приложен изгибающий момент, он отрицателен и равен 
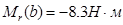(см. рис. 4.2).
|
|
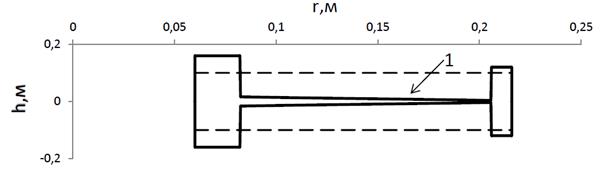
Рис. 4.4. Оптимальная форма диска
(пунктирная линия - толщина начального проекта, сплошная – оптимальный диск)
|
Пример 3. Диск нагружен поперечной распределенной нагрузкой, без ограничения на толщину ступицы и замок (см. рис. 4.5).
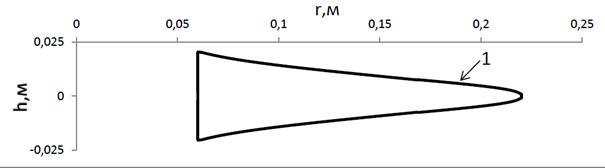
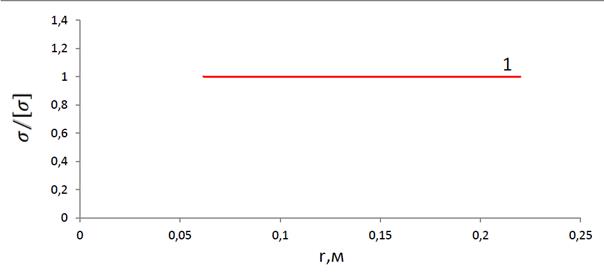
Параметры диска совпадают с параметрами из Примера 1, за исключением того, что отсутствуют конструктивные ограничения по толщине на ступицу и замковое соединение (см. рис. 4.1). В этом случае получается равнопрочный диск (нагрузка подобрана так, что в каждом узле диска эквивалентные напряжения равны напряжению ограничения).
|
Рис. 4.5. Равнопрочный диск
|
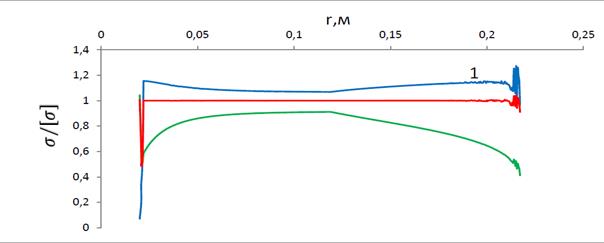
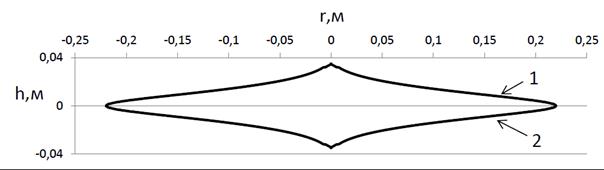
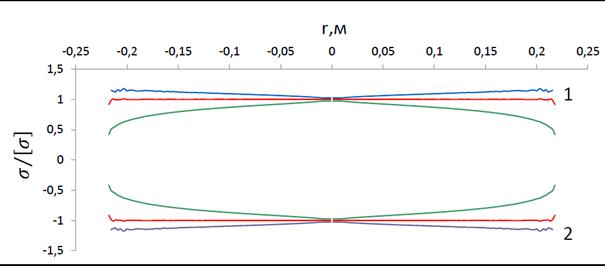
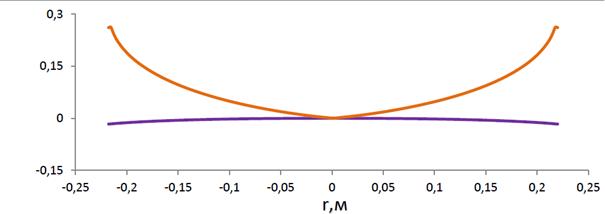
Пример 4. Равнопрочный диск без отверстия (см. рис. 4.6).
Параметры диска совпадают с параметрами диска из Примера 3, за исключением наличия центрального отверстия. На этом примере показаны значения величины изгиба диска и угла поворота нормали для линии, заданной графиком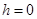 
.
|
Рис. 4.5. Оптимальная форма диска без отверстия
|
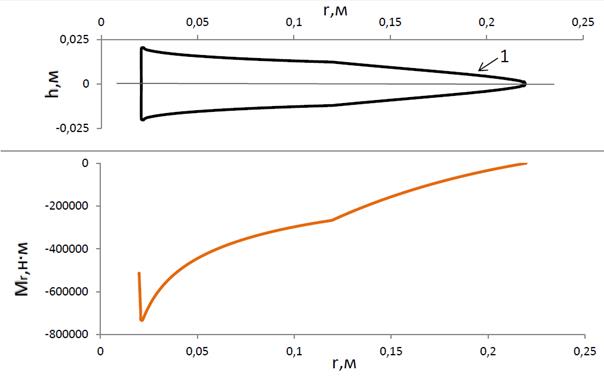
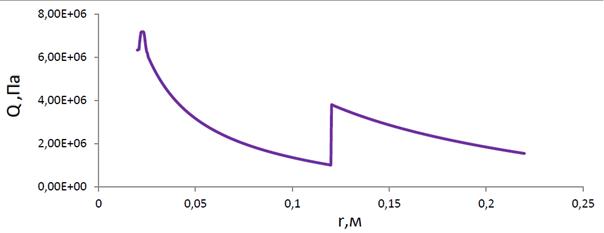
Пример 5. Параметры диска совпадают с параметрами диска из Примера 4, за исключением силы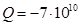 
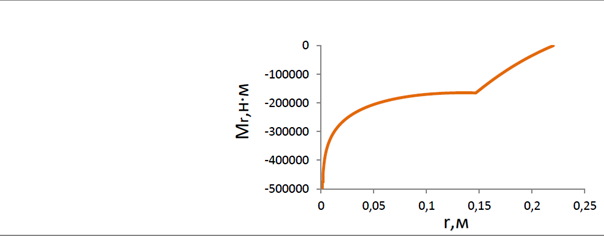
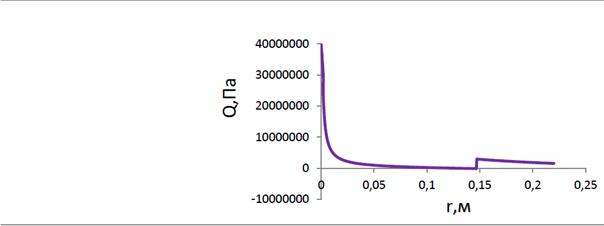
Па, приложенной в точке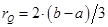 
(см. рис. 4.8). На этом примере показаны эпюры момента и сил для линии, заданной графиком .
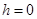Пример 6. Параметры диска совпадают с параметрами диска из Примера 3. К ним добавляется сила 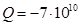Па, приложенная в точке 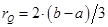, и к внешнему радиусу приложен изгибающий момент, он отрицателен и равен 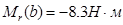(см. рис. 4.9).
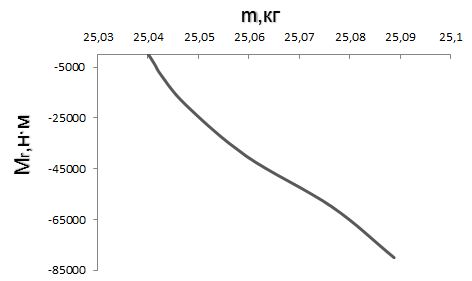
На рис. 4.7 приведены результаты зависимости массы оптимального диска от требуемого радиального момента. Диск взят из Примера 6.
|
Рис. 4.7. Зависимость массы оптимального проекта диска от величины радиального момента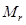 
|
|
| |
| Рис. 4.8. Оптимальная форма диска |
|
|
| |
| Рис. 4.9. Оптимальная форма диска |
|
