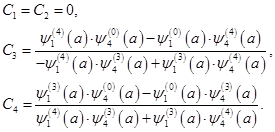3.4. МКЭ применительно к задаче об изгибе круглой пластинки
Расчет диска ведется методом конечных элементов (МКЭ) [9]. МКЭ позволяет избежать численного интегрирования, тем самым уменьшая погрешность вычислений, что, как следствие, приводит к повышению точности. Так же МКЭ позволяет рассчитывать диск на небольшом количестве узлов, что приводит к относительному уменьшению затрат ресурсов вычислительной машины.
Разобьем весь диск на конечные элементы. В расчетах для перехода от функции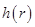 
к вектору параметров проектирования 
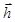использовалась линейная аппроксимация. Отрезок 
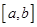разбивается на 
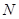равных интервалов 
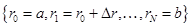, для аппроксимации управляющей функции использовались линейные функции.
Рассмотрим систему (2.24) дифференциальных уравнений первого порядка для диска. Введем обозначения
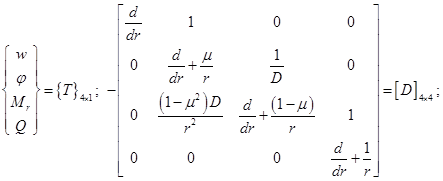
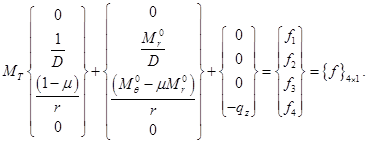(3.23)
И интегрируя по радиусу, получим соотношения МКЭ для уравнения в перемещениях для диска:
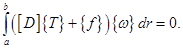
Рассмотрим формирования матрицы системы и вектора нагрузок:
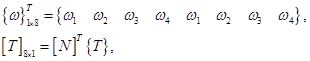
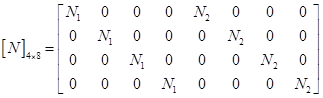- матрица формы, где
.
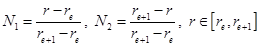Суммируя по всем конечным элементам, найдем
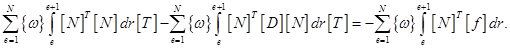
Обозначим
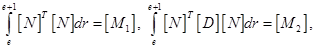
тогда можно записать
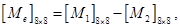
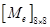- матрица жесткости для одного элемента.
Матрица и правая часть для всей системы формулируются из 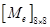и 
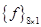как показано на рис. 3.2.
|
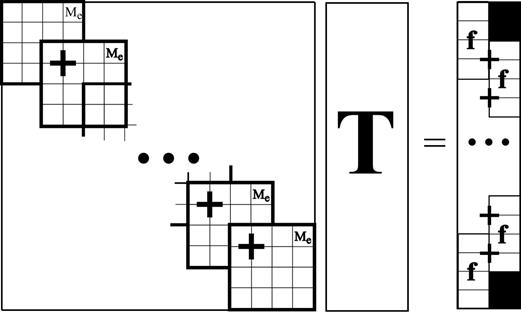
| Рис. 3.2. Формирование общей матрицы системы |
3.5. МКР применительно к задаче об изгибе круглой пластинки
Замена краевой задачи начальной приводит к существенному упрощению решения. Поэтому другой удобный метод решения краевой задачи (2.24) и сопряженной системы (3.15) - метод начальных параметров, основанный на дополнении поставленных для краевой задачи граничных условий в начале участка интегрирования некоторыми параметрами, называемыми начальными [13]. Эти параметры выбираются так, чтобы полученная при этом совокупность начальных условий полностью определяла решение поставленной задачи.
Основная трудность численного решения уравнений (2.24), (3.15) заключается в том, что на основании граничных условий в начальной точке (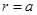 
) бывают известны только некоторые начальные значения функций 
( 
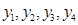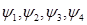в случае сопряженной системы). Остальные же должны быть определены по граничным условиям на наружном крае пластины ( 
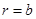) [12].
Пусть дана краевая задача (2.24) с граничными условиями (2.31).
Общий интеграл системы (2.24)
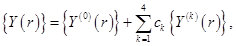(3.24)
где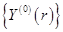 
- частное решение матричного уравнения (2.24), удовлетворяющее нулевым начальным условиям 
; 
- 
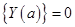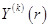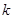-е частное решение соответствующего уравнению (2.24) однородного уравнения 
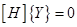, т.е. при нулевом столбце свободных членов
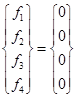,где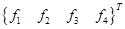 
взято из формулы (3.23),
удовлетворяющее начальным условиям:
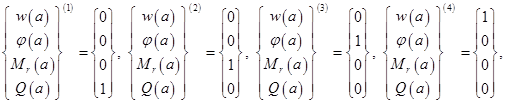
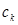- постоянные интегрирования.
Подстановкой полученного по (3.24) решения в условия (2.31) получают систему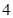 
-х алгебраических уравнений для определения .
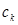Например, для пластины с шарнирной опорой на внутреннем краю:
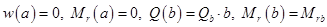
коэффициенты равны:
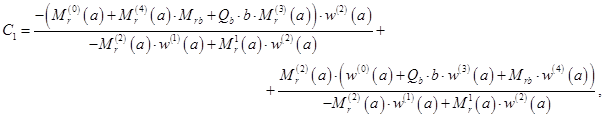
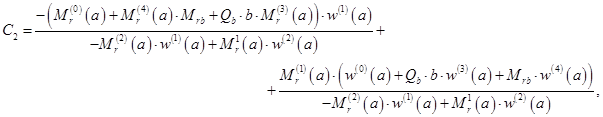
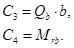
Найденные постоянные подставляют в (3.24), откуда находят решение исходной краевой задачи (2.24), (2.31).
Аналогично решается сопряженная задача (3.15). В ней коэффициенты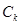 
для граничных условий вида: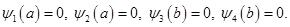 
будут равны:
