Глава 3. Алгоритм оптимизации диска методом чувствительности
3.1. Вывод вариационного уравнения
После того как получена система уравнений для расчета пластинки можно переходить к алгоритму оптимизации диска. Для удобства заменим ограничение (1.1) интегральным соотношением [6]:
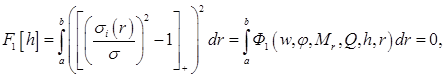 (3.1)
(3.1)
где принято обозначение 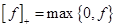 для любой функции
для любой функции 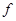 .
.
Метод оптимизации заключается в оценке чувствительности функции цели к параметру управления, которым в нашей задаче является толщина диска [5]. Для реализации этого метода следует взять два похожих диска c толщинами 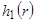 и
и 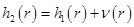 . Отметим, что переход от вектора состояния
. Отметим, что переход от вектора состояния 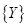 к вектору
к вектору 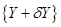 изменит операторное уравнение (2.24)
изменит операторное уравнение (2.24)
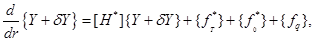 (3.2)
(3.2)
где
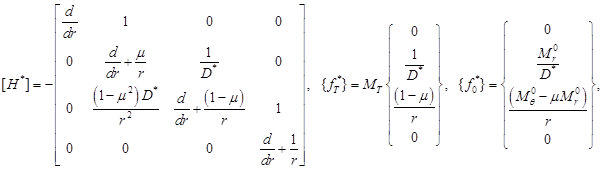
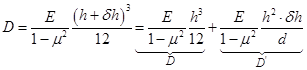 .
.
Тогда представим матрицу 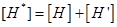 :
:
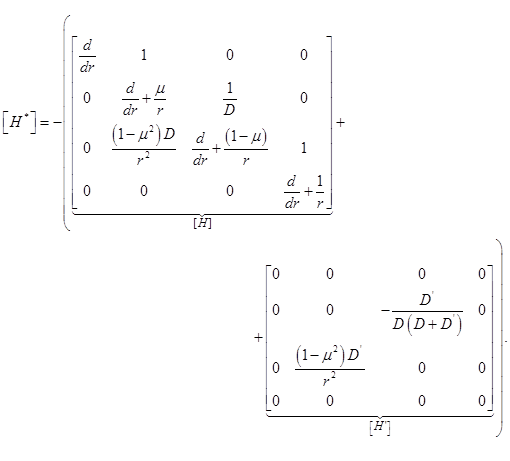 (3.3)
(3.3)
Покажем, что 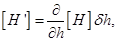 где
где 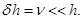 Производная от всех элементов матрицы
Производная от всех элементов матрицы 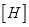 будет равна 0, кроме
будет равна 0, кроме 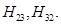 Рассмотрим дифференцирование этих элементов отдельно:
Рассмотрим дифференцирование этих элементов отдельно:
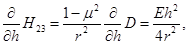 (3.4)
(3.4)
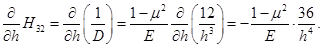 (3.5)
(3.5)
Теперь распишем значения ненулевых элементов матрицы 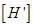 с учетов
с учетов 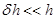 :
:
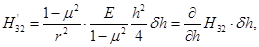 (3.6)
(3.6)
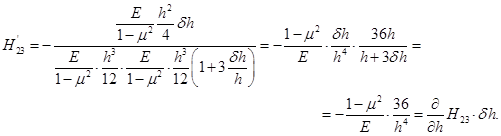 (3.7)
(3.7)
Из (3.5) и (3.6) следует, что 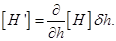 Аналогично получим
Аналогично получим
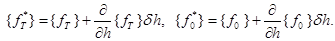
Таким образом, вариационная постановка задачи будет иметь следующий вид: 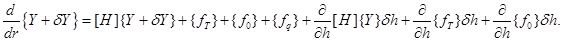 (3.8)
(3.8)
Исключая из (3.8) уравнение (2.24), соответствующее начальному состоянию, получим:
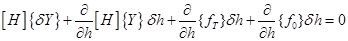
или уравнение в вариациях имеет вид
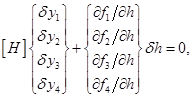 (3.9)
(3.9)
где
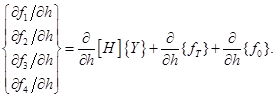 (3.10)
(3.10)
Граничные условия из (2.31) для 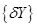 получим следующие
получим следующие
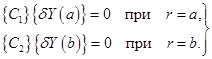 (3.11)
(3.11)
3.2. Расчет градиентов целевой функции и ограничений
Умножим выражение (3.10) на сопряженный вектор 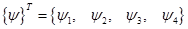 и проинтегрируем на отрезке
и проинтегрируем на отрезке 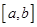
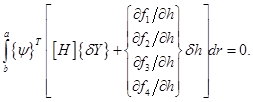 (3.12)
(3.12)
Рассмотрим первое слагаемое интеграла отдельно
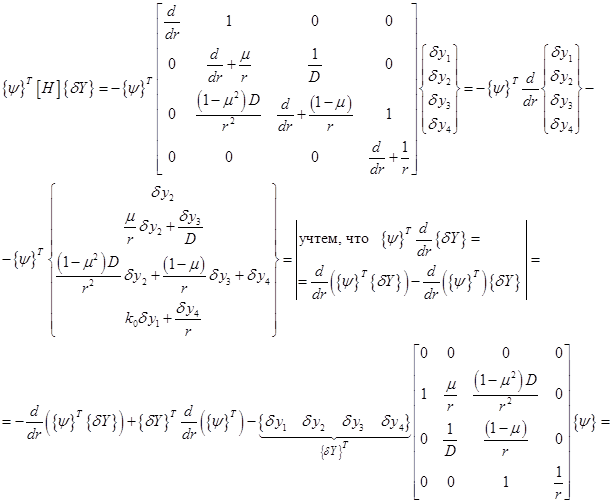
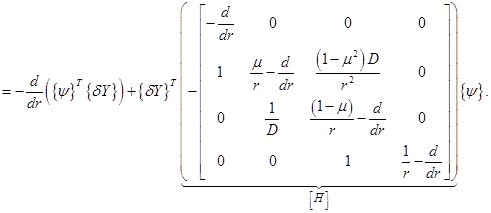
Таким образом,
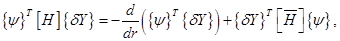 (3.13)
(3.13)
где 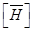 - сопряженный оператор.
- сопряженный оператор.
Воспользовавшись (3.13) представим (3.12) в виде
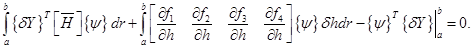 (3.14)
(3.14)
Введем сопряженную систему уравнений
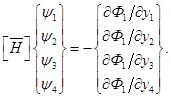 (3.15)
(3.15)
Помня об интегральной записи ограничения (3.1), рассмотрим переход от диска c толщиной 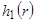 к диску с толщиной
к диску с толщиной 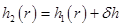 . Функционал
. Функционал 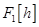 изменяется на
изменяется на
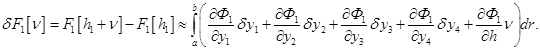 (3.16)
(3.16)
Подставим (3.15) в (3.14) и получим
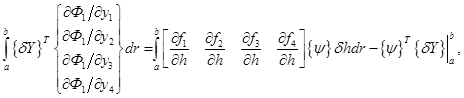
тогда (3.16) примет вид
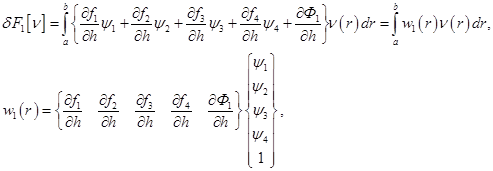 (3.17)
(3.17)
при условии, что в (3.14) 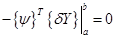 . С учетом (3.11) это накладывает на решение системы (3.15) граничные условия
. С учетом (3.11) это накладывает на решение системы (3.15) граничные условия
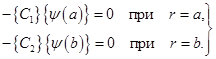
Для определения функции 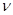 можно решить задачу поиска минимума линейного функционала с интегральными ограничениями
можно решить задачу поиска минимума линейного функционала с интегральными ограничениями
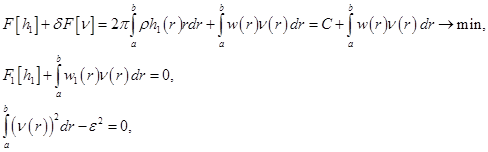 (3.18)
(3.18)
где 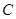 - масса исходного проекта диска (толщиной
- масса исходного проекта диска (толщиной 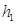 );
); 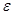 - ограничения, накладываемые на норму изменения
- ограничения, накладываемые на норму изменения 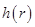 на каждой итерации. От выбора параметра
на каждой итерации. От выбора параметра 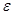 зависит скорость сходимости алгоритма.
зависит скорость сходимости алгоритма.
Задача (3.18) с помощью множителей Лагранжа 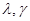 может быть сведена к задаче поиска стационарной точки 7функционала
может быть сведена к задаче поиска стационарной точки 7функционала
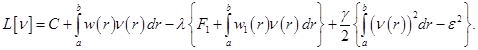 (3.19)
(3.19)
Изменение функционала 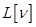 при переходе от функции
при переходе от функции 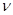 к
к 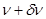 с точностью до линейных слагаемых можно записать следующим образом
с точностью до линейных слагаемых можно записать следующим образом
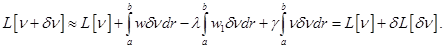 (3.20)
(3.20)
Как и в случае многих переменных, в стационарной точке линейная часть изменения функционала (вариация функционала) должна быть нулевой, т.е.
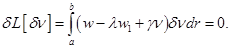
Из этого выражения следует, что
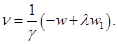 (3.21)
(3.21)
Для определения коэффициента 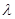 (3.21) подставляется во второе условие (3.18). Окончательное выражение для вариации толщины диска на каждой итерации имеет вид
(3.21) подставляется во второе условие (3.18). Окончательное выражение для вариации толщины диска на каждой итерации имеет вид
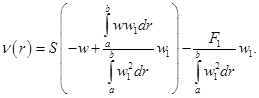 (3.22)
(3.22)
В этой зависимости введен новый параметр 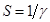 , который совместно с параметром
, который совместно с параметром 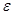 управляет нормой изменения проекта на каждой итерации. От него так же зависит скорость сходимости алгоритма.
управляет нормой изменения проекта на каждой итерации. От него так же зависит скорость сходимости алгоритма.
3.3. Алгоритм метода проекции градиента
На рис. 3.1 представлена блок-схема алгоритма метода проекции градиента. После пересчета толщин следует заново повторять этот алгоритм уже с новыми толщинами, сравнивая напряжения с ограничениями в каждой точке, пока напряжения не станут равны допустимым. Если не налагать конструктивные ограничения по толщине, можно получить оптимальный диск, в каждой точке которого напряжения будут равны предельно допустимым. В зависимости от величины параметров управления скорость сходимости алгоритма будет различной, но не следует пытаться с помощью изменения значений параметров управления ускорить процесс сходимости алгоритма, так как могут возникнуть сильные скачки различных параметров диска из-за слишком большого изменения толщины за одну итерацию.
Расчет диска ведется двумя методами: методом конечных элементов (МКР) [8] и методом конечных разностей (МКР). МКЭ позволяет избежать численного
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Рис. 3.1. Блок-схема алгоритма метода проекции градиента | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
интегрирования, уменьшается погрешность вычислений, что, как следствие, приводит к повышению точности. Так же МКЭ позволяет рассчитывать диск на значительно меньшем количестве узлов по сравнению с МКР, что приводит к относительному уменьшению затрат ресурсов вычислительной машины. Однако МКР значительно выигрывает по времени за счет простоты численного дифференцирования.
МКР проигрывает в точности методу конечных элементов на одинаковом количестве узлов, но за счет увеличения количества узлов в МКР можно добиться одинаковой погрешности этих двух методов при одинаковом количестве затраченного на счет времени. В целом, для достижения одинаковой точности МКР – быстрее, чем МКЭ.










 Решение краевой задачи (2.24)
Решение краевой задачи (2.24)

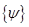
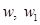 (3.17), (3.18)
(3.17), (3.18)
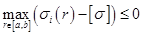
 Условия выполняются
Условия выполняются Условия не выполняются
Условия не выполняются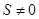
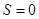
 Проверка сходимости алгоритма
Проверка сходимости алгоритма