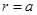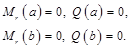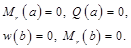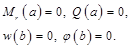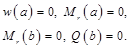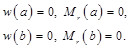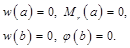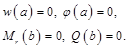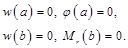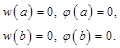Глава 2. Вывод основных уравнений изгиба круглых симметрично нагруженных пластин

Дата: 2025-04-30; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

СОДЕРЖАНИЕ

Глава 1. Введение..................................................................................... ...2

1.1. Общая проблема............................................................................................................ 2

1.2. Структура работы......................................................................................................... 3

1.3. Цель работы................................................................................................................... 4

1.4. Состояние вопроса........................................................................................................ 4

1.5. Задача об изгибе пластинки переменной толщины.................................................. 5

Глава 2. Вывод основных уравнений симметрично нагруженных

пластин......................................................................................... ...7

2.1. Принятые допущения................................................................................................... 7

2.2. Пластина под действием осесимметричной деформации........................................ 7

2.2.1. Определение деформаций и напряжений............................................................. 7

2.2.2. Определение усилий и моментов.......................................................................... 9

2.2.3. Связь деформаций и напряжений с заданными усилиями и моментами........ 10

2.2.4. Условия равновесия пластинки........................................................................... 11

2.3. Уравнение осесимметричного изгиба пластинки переменной толщины............ 13

2.3.1. В общем случае...................................................................................................... 13

2.3.2. При постоянных по толщине параметрах упругости........................................ 15

2.4. Вывод формул для ограничений............................................................................... 16

2.5. Граничные условия..................................................................................................... 16

Глава 3. Алгоритм оптимизации диска методом чувствительности.... ...18

3.1. Вывод вариационного уравнения............................................................................. 18

3.2. Расчет градиентов целевой функции и ограничений............................................. 21

3.3. Алгоритм метода проекции градиента..................................................................... 24

3.4. МКЭ применительно к задаче об изгибе круглой пластинки............................... 26

3.5. МКР применительно к задаче об изгибе круглой пластинки................................ 28

Глава 4. Результаты оптимизации......................................................... ...31

4.1. Описание программы................................................................................................. 31

4.2. Примеры расчетов оптимальных дисков................................................................. 32

Глава 5. Организационно-экономическая часть................................... ...42

5.1. Организация и планирование проведения НИР..................................................... 42

5.1.1. Расчет трудоемкости и составление календарного графика............................. 43

5.2. Расчет себестоимости НИР........................................................................................ 48

5.3. Итоговые данные........................................................................................................ 52

Глава 6. Экологическая и промышленная безопасность...................... ...53

6.1. Проектирование оптимальных условий труда инженера-программиста............. 53

6.1.1. Анализ условий труда на рабочем месте............................................................ 53

6.1.2. Требование к рабочим местам оборудованными ПК........................................ 55

6.1.3. Требование к ПЭВМ............................................................................................. 59

6.1.4. Требование к помещениям для работы с ПЭВМ................................................ 60

6.2. Требования к производственной среде.................................................................... 62

6.2.1. Требование к микроклимату на рабочих местах, оборудованных ПЭВМ...... 62

6.2.2. Требования к уровням шума, вибрации и акустическим средствам отображения информации на рабочих местах, оборудованных ПЭВМ............................................................. 63

6.2.3. Требования к освещению на рабочих местах, оборудованных ЭВМ.............. 65

6.2.4. Требования к уровням электромагнитных полей на рабочих местах, оборудованных ЭВМ 68

6.2.5. Требования к организации режимов труда и отдыха........................................ 69

6.2.6. Требования к организации медицинского обслуживания пользователей

ВДТ и ПЭВМ.......................................................................................................... 69

6.3. Определение освещенности...................................................................................... 70

6.3.1. Описание места, в котором располагается рабочее место................................ 70

6.3.2. Расчет систем искусственного освещения.......................................................... 70

6.4. Ртутьсодержащие отходы потребления и их утилизация....................................... 74

6.5. Характеристики ламп................................................................................................. 77

Заключение................................................................................................ 79

Список литературы................................................................................... 80

ГЛАВА 1. ВВЕДЕНИЕ

1.1. Общая проблема

Целью инженерной деятельности всегда было получение наиболее рациональных конструкций и деталей. Создание новых конструкций обычно осуществляется постепенным улучшением существующей конструкции. До широкого внедрения вычислительной техники в практику расчетной деятельности оптимизация конструкции реализовывалась на основе проб и ошибок. Конструктор варьировал форму, материал детали и исследовал влияние внесенных изменений на характеристику конструкции.

В настоящее время технологическая конкуренция вынуждает искать пути уменьшения времени разработки новых конструкций, повышения качества и надежности разрабатываемого изделия. Поэтому оптимальное проектирование занимает одну из ключевых позиций при создании современных конкурентоспособных конструкций.

Формулирование технических требований в виде утверждений теории математического программирования является основным подходом оптимального проектирования. Это позволяет свести задачу оптимизации конструкции к математической задаче поиска экстремума.

При постановке задач оптимизации используется параметризованный чертеж (эскиз разрабатываемой конструкции) с рядом размеров, допускающих варьирование в заданных пределах. Они называются параметрами проектирования. Для формулировки задачи оптимизации выбирается характеристика, подлежащая минимизации или максимилизации и набор ограничений для обеспечения работоспособности конструкции. Решением задачи является набор значений параметров, удовлетворяющий заданным критериям и ограничениям, наложенным на конструкцию.

Важное значение имеет используемый алгоритм поиска оптимального решения, так как задачи оптимального проектирования характеризуются сложными, неявно заданными функциями и большой размерностью.

Множество алгоритмов математического программирования, решающих задачи оптимального проектирования, реализовано в виде программных библиотек или в качестве части пакетов универсальных программных комплексов. Общим недостатком этих алгоритмов является низкая скорость сходимости и высокая вероятность получить неоптимальный результат.

Более совершенные алгоритмы оптимизации требуют расчета не только значений функций, но и вычисления их производных. Анализом на чувствительность принято называть задачу исследования поведения свойств системы при небольшом варьировании значений параметров проектирования в окрестности заданной точки.

Анализ чувствительности системы позволяет выявить параметры, оказывающие наибольшее влияние на свойства конструкции и благодаря этому вычислить наиболее эффективные изменения параметров проектирования для улучшения свойств системы.

1.2. Структура работы

В первой главе рассматриваются общие вопросы, касающиеся истории исследования данной темы, основные проблемы и технические задачи. Описывается цель проведения исследования. Приводится общая постановка задачи, накладываются конструктивные ограничения.

Во второй главе указываются принятые допущения, выводятся основные уравнения для изгиба круглой симметрично нагруженной пластины переменной толщины, уравнения для прочностных ограничений. Записываются граничные условия.

В третьей главе разрабатывается алгоритм оптимизации диска методом чувствительности. Рассчитываются градиенты целевой функции и ограничений. Описывается МКЭ применительно к поставленной задаче.

В четвертой главе описывается разработанная программа, приводятся результаты оптимизации, примеры расчетов оптимальных дисков при различных граничных условиях.

В пятой главе представлена организационно-экономическая информация о проведенной работе.

В шестой главе приведены оптимальные условия труда инженера-программиста, рассчитана освещенность рабочего места, представлена утилизация ртутьсодержащих отходов.

1.3. Цель работы

Целью данной работы является разработка и применение эффективного алгоритма анализа чувствительности для оптимизации формы круглых осесимметричных пластин.

В настоящей работе приводится единый алгоритм метода проекции градиента, позволяющий однотипно решать задачи оптимизации формы круглых осесимметричных пластин

Данная работа может быть применима при создании программных комплексов для эффективной оптимизации конструкций.

1.4. Состояние вопроса

Проблема оптимизации формы круглых осесимметричных пластин решается различными способами. Наиболее совершенный алгоритм оптимизации формы – метод проекции градиента, потому что в этом методе, независимо от количества параметров проектирования, на каждой итерации проводятся всего два расчета напряженно-деформированного состояния, следовательно, можно не накладывать никаких ограничений на количество управляющих параметров. В методе проекции градиента не используется численное дифференцирование, что существенно уменьшает погрешность относительно других алгоритмов. Так же существенным плюсом является то, что в этом методе величина шага определяется пользователем произвольно и может варьироваться. Это обеспечивает более надежную сходимость алгоритма.

Метод проекции градиента в общем случае изложен в [6]. При отсутствии конструктивных и технологических ограничений и градиента температур есть возможность спроектировать равнопрочную круглую пластину [2]. В [3] изложен алгоритм оптимизации формы осесимметричной пластины постоянного объема с изгибающими моментами и распределенными поперечными нагрузками при условии того, чтобы первая собственная частота поперечных колебаний пластины принимала оптимальное значение при определенных вариантах граничных условий. Так же в [3] приводятся формы оптимальных дисков при определенных начальных условиях. Проблема оптимального проектирования диска с центростремительной нагрузкой и конструктивными и технологическими ограничениями методом проекции градиента подробно решена в [4].

1.5. Задача об изгибе пластинки переменной толщины

Задача оптимизации круглой пластинки заключается в минимизации ее массы при выполнении ограничений на напряженно-деформированное состояние. В простейшем случае геометрия пластинки задается функцией толщины от радиуса 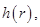которая и является параметром управления.

Функцией качества, подлежащей минимизации, является масса пластинки. Для обеспечения технологичности конструкций, на проект пластинки накладываются геометрические или технологичные ограничения 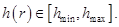Требование работоспособности конструкции выражается в прочностном ограничении 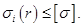Все эти требования к проекту пластинки составляют оптимизационную задачу

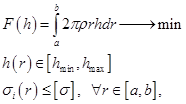(1.1)

здесь 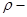плотность материала пластинки; 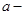внутренний радиус пластинки; 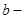внешний радиус пластинки; 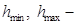конструктивные и технологические ограничения на толщину пластинки; 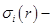интенсивность напряжений; 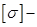допускаемые напряжения.

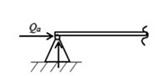
В данной работе рассматривается круглая изотропная пластинка (далее в качестве примера круглой пластины будем рассматривать диск ГТД, см. рис. 1) симметричная относительно своей срединной поверхности. Толщина 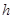предполагается малой по сравнению с наружным радиусом 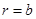. Силы, действующие на диск, равномерно распределены по поверхности и направлены перпендикулярно радиусу. Температура считается постоянной по толщине.

Напряженное состояние в пластинке считается двумерным и осесимметричным, напряжения равномерно распределены по толщине.

Рис. 1.1. Меридиональное сечение диска, симметричного относительно своей срединной поверхности

Далее будут рассмотрены расчет напряженно-деформированного состояния круглой пластины и вывод формул для алгоритма оптимизации методом проекции градиента.

ГЛАВА 2. ВЫВОД ОСНОВНЫХ УРАВНЕНИЙ ИЗГИБА КРУГЛЫХ СИММЕТРИЧНО НАГРУЖЕННЫХ ПЛАСТИН

2.1. Принятые допущения

Теория изгиба пластин и оболочек основана на некоторых упрощающих предположениях [1]:

1) толщина пластинки 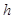достаточно мала по сравнению с другими ее размерами, что значит 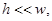где 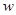- прогиб пластинки;

2) гипотеза Кирхгофа (о неизменности нормали) гласит, что точки, расположенные на некоторой прямой, нормальной к срединной поверхности до деформации, после деформации снова образуют прямую, нормальную к деформированной поверхности;

3) нормальные напряжения в сечениях параллельных срединной поверхности малы по сравнению с изгибными напряжениями, т.е. отсутствует надавливание между слоями пластины.

2.2. Пластина под действием осесимметричной деформации

2.2.1. Определение деформаций и напряжений

С учетом указанных допущений при осесимметрической деформации (рис. 2.1) точки пластинки получают радиальные смещения [6]

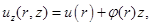(2.1)

где 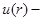радиальное смещение, 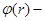угол поворота нормали в точках основной поверхности.

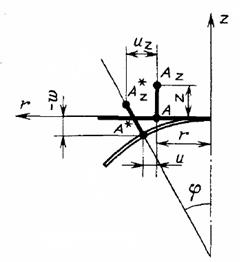
Рис. 2.1. Прогиб пластины

Радиальная и окружная деформация равны

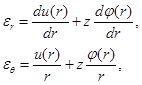(2.2)

или

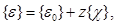(2.3)

где

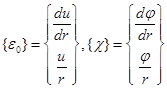
- векторы деформации основной поверхности и кривизны.

При упругом деформировании изотропного материала имеем

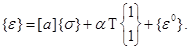(2.4)

В последнем равенстве 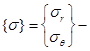вектор напряжений, 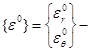вектор дополнительных деформаций, 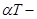температурная деформация. Матрица упругости материала

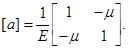
Как и раньше, 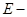модуль упругости, 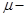коэффициент Пуассона. Из равенств (2.4) и (2.3) вытекает

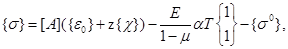(2.5)

где

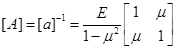
- матрица жесткости материала,

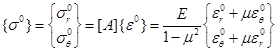(2.6)

- условные дополнительные (начальные) напряжения. По физическому смыслу напряжения 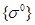соответствуют (с обратным знаком) дополнительным деформациям 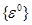при полном стеснении плоской деформации элемента.

2.2.2. Определение усилий и моментов

Рассмотрим выделенную призму (рис. 2.2). Усилия и моменты на единицу длины сечения будут равны

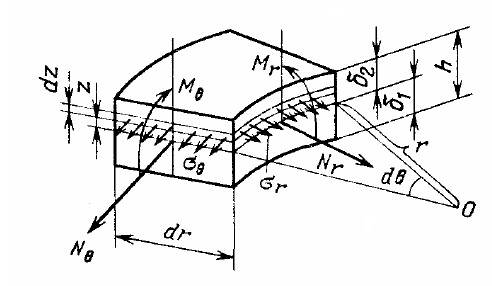
Рис. 2.2. Напряжения, действующие в элементарной призме

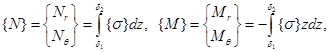
где 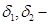расстояния основной поверхности (плоскости) от торцевых поверхностей пластинки. С помощью соотношения (2.5) получим:

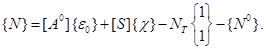(2.7)

Симметричные матрицы

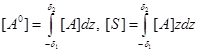
содержат элементы

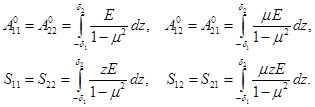(2.8)

Температурные и дополнительные усилия

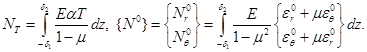(2.9)

Для моментов будем иметь

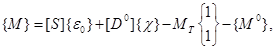(2.10)

где матрица

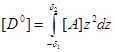
содержит следующие элементы:

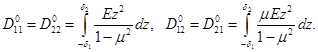(2.11)

Температурный и дополнительный моменты:

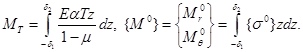(2.12)

2.2.3. Связь деформаций и напряжений с заданными усилиями и моментами

Пусть основная поверхность выбрана произвольным образом (удобно принять ее совпадающей со срединной поверхностью). Объединяя (2.7) и (2.10) с помощью блочных векторов и матриц, запишем

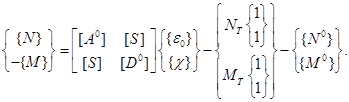(2.13)

Далее находим

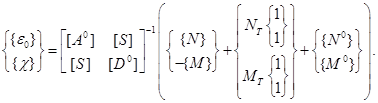(2.14)

Получив деформации по формуле (2.14), определяем напряжения из (2.5).

2.2.4. Условия равновесия элемента пластинки

Считая малым отклонение срединной поверхности от плоскости, т.е. 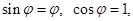выведем условия равновесия (рис.3):

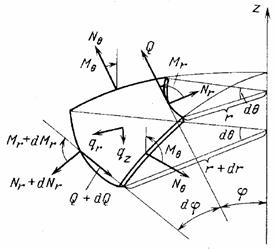
Рис. 2.3. Усилия и моменты, приложенные к элементу пластинки

получим следующие условия равновесия [1,7]:

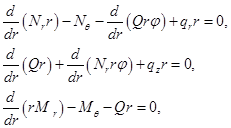(2.15)

где

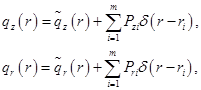
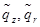- распределенные усилия на единицу площади срединной поверхности; 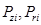- распределенные вдоль окружности радиуса 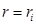осевые и радиальные силы; 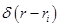- дельта-функция. Усилие 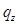направлено как внешнее давление. Уравнения (2.15) справедливы и для пластики с начальными отклонениями 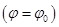. В большинстве практических задач можно пренебречь третьим членов в первом уравнении из (2.15).

2.3. Уравнение осесимметричного изгиба пластинки переменной толщины

2.3.1. В общем случае

Составим уравнение равновесия недеформированного состояния (т.е. в формуле (2.15) положим ):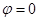

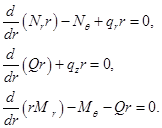(2.16)

Для упрощения предположим, что коэффициент Пуассона не меняется по толщине пластинки (вдоль радиуса он может быть переменным) 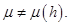Основная поверхность (плоскость) выбирается из условия

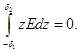
Тогда матрицы 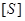и 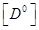примут вид

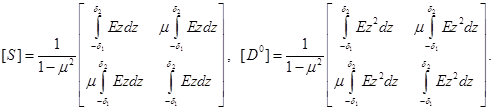
При рассмотрении только изгиба ( ) уравнение (2.10) приведется к следующим простым соотношениям

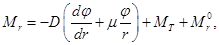(2.17)

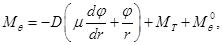(2.18)

где

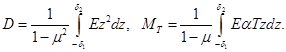
Из соотношений (2.17) и (2.18) получаем

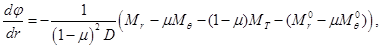(2.19)

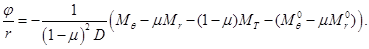(2.20)

Уравнение равновесия для моментов из (2.16) представим в виде

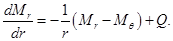(2.21)

Внося значение 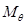из (2.20) в (2.19) и (2.21), получаем дифференциальное уравнение изгиба пластинки

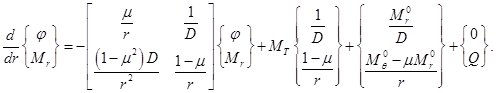(2.22)

Составим систему уравнений. Определим прогиб 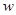как

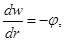(2.23)

Положительное направление прогиба вдоль оси Z.

Соберем уравнения (2.23), (2.22) и выражение для 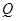из (2.16) и запишем получившуюся систему в матричном виде:

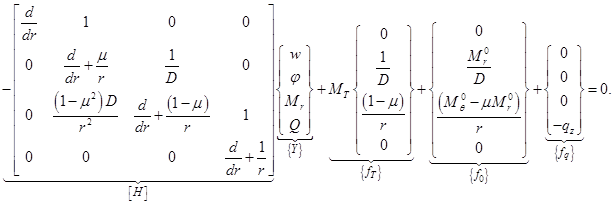
Коротко эта система представима в операторном виде

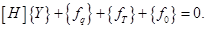(2.24)

2.3.2. При постоянных по толщине параметрах упругости

Пусть параметры упругост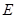и и 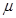постоянны по толщине пластины (они могут быть переменными вдоль радиуса), тогда целесообразно выбрать [7]

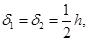
где 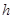- толщина пластинки. Тогда матрицы упруго-геометрических характеристик могут быть значительно упрощены

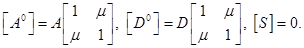
Цилиндрические жесткости на растяжение и изгиб:

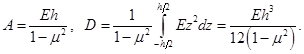(2.25)

Температурный и дополнительный моменты:

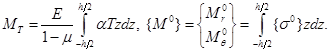(2.26)

2.4. Вывод формул для ограничений

Ограничения на эквивалентные напряжения из формулы (1.1) представим в виде

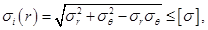(2.27)

где 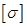- допускаемое напряжение на радиусе, 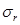и 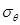выражаются из уравнений (2.5), (2.17) и (2.22):

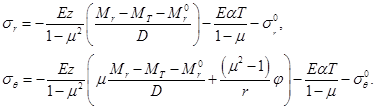(2.28)

При постоянных по толщине параметрах упругости и при линейном изменении температуры по толщине диска [2]:

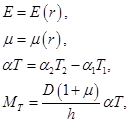(2.29)

где 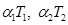- температурные деформации на поверхности диска, (2.28) примет вид

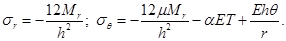(2.30)

2.5. Граничные условия

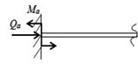
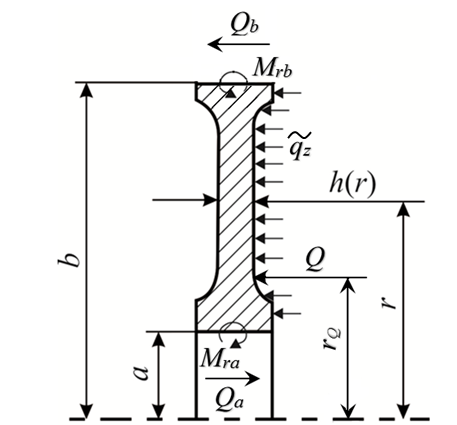
Задача (2.24) является краевой и состоит из четырех дифференциальных уравнений первого порядка. Следовательно, должны быть заданы четыре краевых условия: два – на внутреннем радиусе и два – на внешнем [13]:

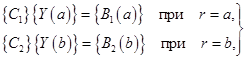(2.31)

где 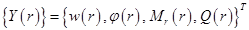; 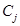и 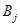- матрицы столбцы размером : , .

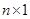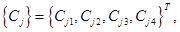
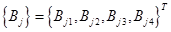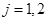Например, в книге [1] предлагается задать два статических параметра на внутреннем радиусе 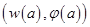, а на внешнем радиусе – два динамических параметра .

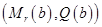В примерах [2] граничными условиями определяется поперечная сила на обоих радиусах 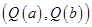и задаются угол поворота нормали на внутреннем радиусе и момент на внешнем.

Рассмотрим отдельно разные способы опирания пластины на контуре [12]:

1. свободный край;

2. свободно опертый край;

3. жестко защемленный край.

При жестком закреплении нет угловых и линейных перемещений .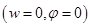

Свободное опирание (подвижная/неподвижная шарнирные опоры) исключает линейное перемещение в вертикальном направлении, но при этом возможен поворот по опертой стороне.

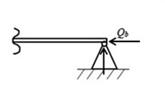
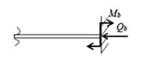
Способы задания граничных условий приведены в табл. 2.1.

	Таблица 2.1
Способы задания граничных условий
на внешнем радиусе     на внутреннем радиусе		свободный край	свободное опирание пластины на контуре[1]	жестко защемленный край
свободный край
свободное опирание пластины на контуре1
жестко защемленный край