Вычислите частные производные, первого порядка
164. 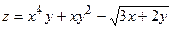 ;
;
165. 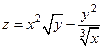 ;
;
166. 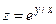 ;
;
167. 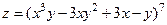 ;
;
168. 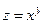 ;
;
169. 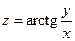 ;
;
170. 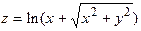 ;
;
171. 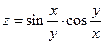 ;
;
172. 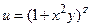 .
.
В задачах 164, 165, 166, 167, 168, 170 вычислите частные производные второго порядка.
173. Вычислите 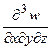 , если .
, если . 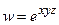 .
.
174. Вычислите 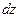 , если
, если 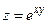 и
и 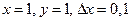 ,
, 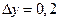 .
.
175. Вычислите 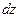 и
и 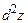 , если а)
, если а) 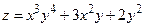 ,
,
б) 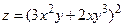 .
.
176. Вычислите приближенно с помощью дифференциала 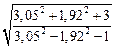 .
.
177. Убедитесь, что функция 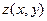 имеет в точке М0 экстремум и определите его тип
имеет в точке М0 экстремум и определите его тип
а) 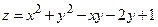 , М0
, М0 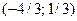 ;
;
б) 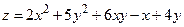 , М0(8,5; –5,5);
, М0(8,5; –5,5);
в) 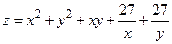 , М0
, М0 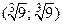 .
.
Исследуйте на экстремум функции:
178. 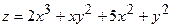 ;
;
179. 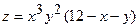 , если x ¹ 0, y ¹ 0;
, если x ¹ 0, y ¹ 0;
180. 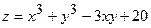 ;
;
181. 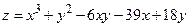
182. 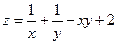 ;
;
183. 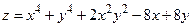 ;
;
184. 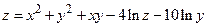
185. 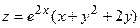 ;
;
186. 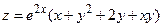 ;
;
187. 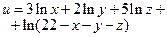 .
.
Найдите наименьшее и наибольшее значения функции:
188. 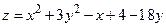
а) 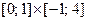 ,
,
б) 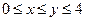 ;
;
189. 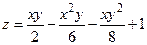 а) в
а) в 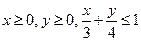 ,
,
б) 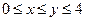 ;
;
190. 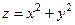 в круге
в круге 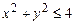 ;
;
191. 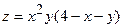 в треугольнике x = 0, y = 0, x + y = 6.
в треугольнике x = 0, y = 0, x + y = 6.
Исследуйте функции на условный экст ремум:
192. 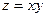 , при
, при 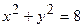 ;
;
193. 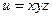 , если
, если 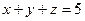 ,
, 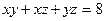 .
.
Вычислите производные параметрически заданных функций:
194. 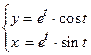 ,
, 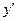 ;
;
195. 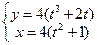 ,
, 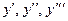 ;
;
196. 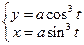 ,
, 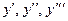 ;
;
197. 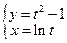 ,
, 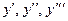 ;
;
198. 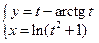 ,
, 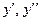 .
.
199. Докажите, что функция y(x), заданная параметрически 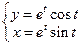 , удовлетворяет соотношению
, удовлетворяет соотношению 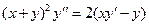 .
.
Вычислите производные первого и второго порядка от неявно заданных функций
200. 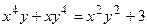 ;
;
201. 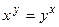 ;
;
202. 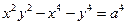 ;
;
203. 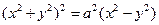 ;
;
204. 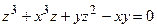 ;
;
205. 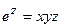 , (
, ( 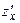 ,
, 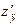 ).
).
Найдите градиент функции
206. 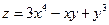 в точке М0(1; –2);
в точке М0(1; –2);
207. 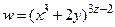 в точке М0(2; 3; 2).
в точке М0(2; 3; 2).
208. Вычислите производную функции в точке M0 по направлению 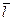 , если
, если
а) 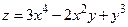 , М0(1; 2),
, М0(1; 2), 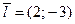 ;
;
б) 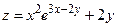 М0(2; 3),
М0(2; 3), 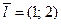 ;
;
в) 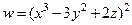 , М0(2; 3; 1),
, М0(2; 3; 1), 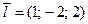 .
.
209. Найдите 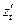 , если а)
, если а) 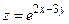 и
и 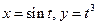 ; б)
; б) 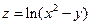 и
и 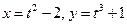 .
.
210. Найдите 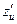 и
и 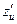 , если в)
, если в) 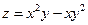 и
и 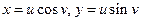 .
.
211. Неявные функции 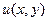 и
и 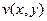 заданы системой уравнений
заданы системой уравнений 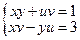 . Найдите частные производные и полные дифференциалы первого и второго порядка, если
. Найдите частные производные и полные дифференциалы первого и второго порядка, если 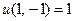 и
и 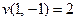 .
.
212. Определите углы, под которыми пересекаются кривые 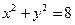 и
и 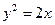 .
.
213. Покажите, что гиперболы 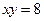 и
и 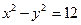 пересекаются под прямым углом.
пересекаются под прямым углом.
214. Сумма ребер прямоугольного параллелепипеда равна а. Каковы размеры параллелепипеда наибольшего объема?
215. Определите размеры цилиндрического сосуда наибольшей вместимости с данной поверхностью S?
216. Найдите прямоугольный параллелепипед наибольшего объема, если длина его диагонали равна d?
*143 (x=l/4)








