Вычислите дифференциалы функций
Вычислите производные:
1. 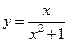 ;
;
2. 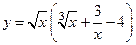 ;
;
3. 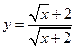 ;
;
4. 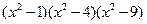 ;
;
5. 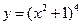 ;
;
6. 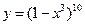 ;
;
7. 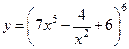 ;
;
8. 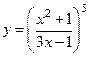 ;
;
9. 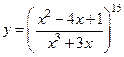 ;
;
10. 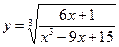 ;
;
11.  ;
;
12. 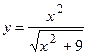 ;
;
13. 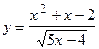 ;
;
14. 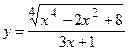 ;
;
15. 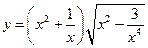 ;
;
16. 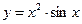 ;
;
17. 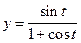 ;
;
18. 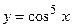 ;
;
19. 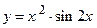 ;
;
20. 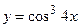 ;
;
21. 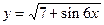 ;
;
22. 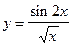 ;
;
23. 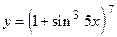 ;
;
24. 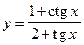 ;
;
25. 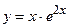 ;
;
26. 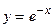 ;
;
27. 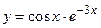 ;
;
28. 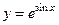 ;
;
29. 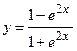 ;
;
30. 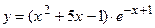 ;
;
31. 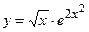 ;
;
32. 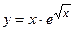 ;
;
33. 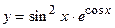 ;
;
34. 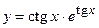 ;
;
35. 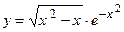 ;
;
36. 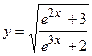 ;
;
37. 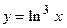 ;
;
38. 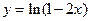 ;
;
39. 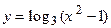 ;
;
40. 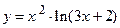 ;
;
41. 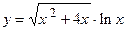 ;
;
42. 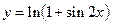 ;
;
43. 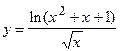 ;
;
44. 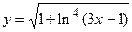 ;
;
45. 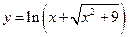 ;
;
46. 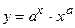 ;
;
47. 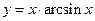 ;
;
48. 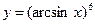 ;
;
49. 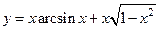 ;
;
50. 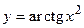 ;
;
51. 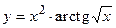 ;
;
52. 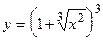 ;
;
53. 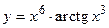 ;
;
54. 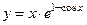 ;
;
55. 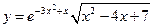 ;
;
56. 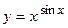 ;
;
57. 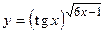 ;
;
58. 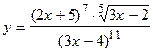 ;
;
Вычислите производные указанных порядков:
59. 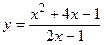 ,
, 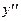 ;
;
60. 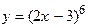 ,
, 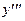 ;
;
61. 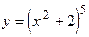 ,
, 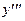 ;
;
62. 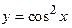 ,
, 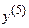 ;
;
63. 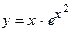 ,
, 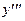 ;
;
64. 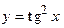 ,
, 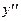 ;
;
65. 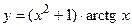 ,
, 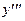 ;
;
66. 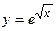 ,
, 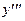 ;
;
67. 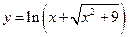 ,
, 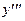 .
.
68. Докажите, что функция 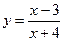 удовлетворяет соотношению
удовлетворяет соотношению 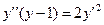 .
.
69. Докажите, что функция 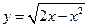 удовлетворяет соотношению
удовлетворяет соотношению 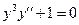 .
.
70. Найдите приращение и дифференциал функции
а) 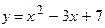 в точке хо=3, если
в точке хо=3, если 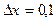 и если
и если 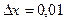 ;
;
б) 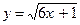 в точке хо=4, если
в точке хо=4, если 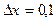 .
.
Вычислите дифференциалы функций
71. 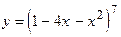 ;
;
72. 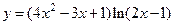 ;
;
73. 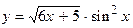 .
.
74. Вычислите приближенно с помощью дифференциала а) 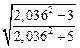 , б)
, б) 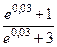 ; в)
; в) 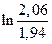 ; г)
; г) 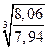 .
.
Вычислите пределы по правилу Лопиталя
75. 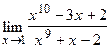 ;
;
76. 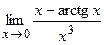 ;
;
77. 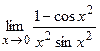 ;
;
78. 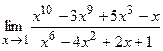 ;
;
79. 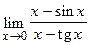 ;
;
80. 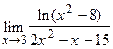 ;
;
81. 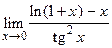 ;
;
82. 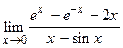 ;
;
83. 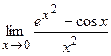 ;
;
84. 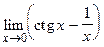 ;
;
85. 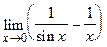 ;
;
86. 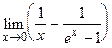 ;
;
87. 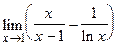 ;
;
88. 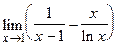 ;
;
89. 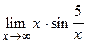 ;
;
90. 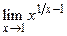 ;
;
91. 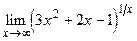 .
.
92. 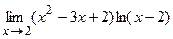 .
.
93. Проверьте, что существует 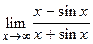 , но его нельзя вычислить по правилу Лопиталя.
, но его нельзя вычислить по правилу Лопиталя.
94. Напишите уравнение касательной к графику функции 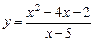 в точке с абсциссой
в точке с абсциссой 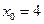 .
.
95. Напишите уравнение касательной к графику функции 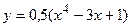 в точке с абсциссой
в точке с абсциссой 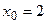 .
.
96. Найдите угловой коэффициент касательной, проведенной к графику функции 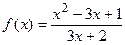 в точке с абсциссой
в точке с абсциссой 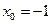 .
.
97. Напишите уравнение касательной к графику функции 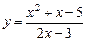 в точке с абсциссой
в точке с абсциссой 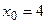 .
.
98. Найдите точку пересечения касательной к графику функции 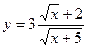 в точке (4; 3) с осью OY.
в точке (4; 3) с осью OY.
99. Укажите точки, в которых касательная к графику 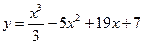 параллельна прямой
параллельна прямой 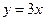 .
.
100. Найдите угол между касательной к графику функции 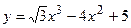 в точке с абсциссой
в точке с абсциссой 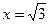 и положительным направлением оси OX.
и положительным направлением оси OX.
101. Покажите, что касательная в любой точке кривой 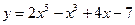 наклонена к оси ОХ под острым углом.
наклонена к оси ОХ под острым углом.
102. Тело движется по закону 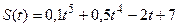 (путь – в метрах, время – в секундах). Найдите скорость и ускорение тела в момент t = 2.
(путь – в метрах, время – в секундах). Найдите скорость и ускорение тела в момент t = 2.
103. Тело движется по закону 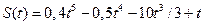 (путь – в метрах, время – в секундах). Найдите ускорение тела в момент t = 3. В какой момент времени его скорость будет максимальна.
(путь – в метрах, время – в секундах). Найдите ускорение тела в момент t = 3. В какой момент времени его скорость будет максимальна.
Найдите интервалы монотонности и точки экстремума функций:
104. 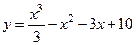 ;
;
105. 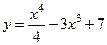 ;
;
106. 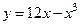 ;
;
107. 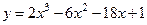 ;
;
108. 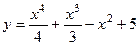 ;
;
109. 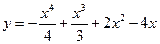 ;
;
110. 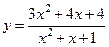 ;
;
111. 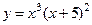 ;
;
112. 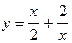 ;
;
113. 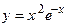 ;
;
114. 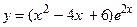 ;
;
115. 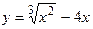 ;
;
116. 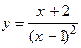 ;
;
117. 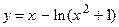 ;
;
118. 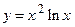 ;
;
119. 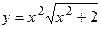 ;
;
120. 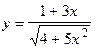
121. 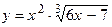 ;
;
122. 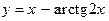 ;
;
123. 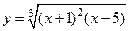 ;
;
124. 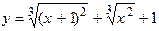 .
.
Найдите сумму значений функций в точках минимума:
125. 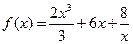 ;
;
126. 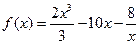 ;
;
127. 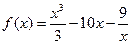 ;
;
128. 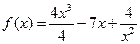 .
.
Найдите наименьшее и наибольшее значения функции на заданном интервале:
129. 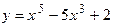 на [–2;3];
на [–2;3];
130. 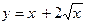 на [0; 9];
на [0; 9];
131. 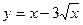 на [0; 4];
на [0; 4];
132. 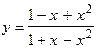 на [0; 1].
на [0; 1].
133. Число 39 разложите на два слагаемых так, чтобы сумма их квадратов была наименьшей.
134. Решеткой длиной 120 м нужно огородить примыкающую к дому прямоугольную площадку наибольшей площади. Определите размеры площадки.
135. Какое число, будучи сложенным с обратным ему, дает наибольшую сумму.
136. Определите размеры открытого бассейна с квадратным дном и объемом 32 м3 (V м3) так, чтобы на облицовку стен и дна пошло наименьшее количество материала.
137. Каковы должны быть размеры прямоугольника, длина диагонали которого равна 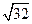 (а), чтобы его площадь была наибольшей?
(а), чтобы его площадь была наибольшей?
138. Какова должна быть высота прямоугольного параллелепипеда с квадратным основанием и суммой длин ребер 24 см, чтобы его объем был наибольшим?
139. Боковые стороны и меньшее основание трапеции равны 10 см. Определите ее большее основание так, чтобы площадь трапеции была наибольшей.
140. Сечение тоннеля имеет форму прямоугольника, завершенного полукругом. Периметр сечения 18 м. При каком радиусе площадь сечения будет наибольшей?
141. Балка длиной l прогибается под действием нагрузки Q, находящейся в ее середине, причем правый конец балки укреплен, а левый свободно лежит на опоре. Прогиб балки в точке, лежащей на расстоянии x от ее левого конца задается формулой 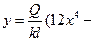
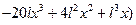 . Найдите наибольший прогиб балки.
. Найдите наибольший прогиб балки.
142. Батарея с электродвижущей силой E и внутренним сопротивлением r замкнута проводником с сопротивлением R. Мощность получающегося тока W задается формулой 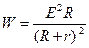 . При каком значении R мощность тока будет наибольшей?
. При каком значении R мощность тока будет наибольшей?
143.  Суммарный расход воды, вытекающей через отверстие в стене, определяется по формуле
Суммарный расход воды, вытекающей через отверстие в стене, определяется по формуле 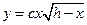 , где х – диаметр отверстия, h – глубина его нижней точки, с – постоянная. При каком диаметре отверстия расход воды будет наибольшим?
, где х – диаметр отверстия, h – глубина его нижней точки, с – постоянная. При каком диаметре отверстия расход воды будет наибольшим?
144. Баржу, палуба которой на 4 м ниже пристани, подтягивают к ней при помощи каната, наматываемого на ворот со скоростью 2 м/сек. С каким ускорением движется баржа в момент, когда она удалена от пристани на расстояние 8 м по горизонтали?
145. Лестница длиной а, прислоненная к вертикальной стене падает, скользя одним концом о стену, а другим о пол. С какой скоростью движется верхний конец лестницы, когда нижний конец, двигающийся с постоянной скоростью v, отстоит от нее на расстоянии b?
146. Человек ростом 1,7 м удаляется от источника света, находящегося на высоте h м (h >1,7) со скоростью 5 км/ч. Определите скорость перемещения тени от его головы.
147. Вблизи завода А проводится по прямой к городу В железная дорога. Под каким углом к железной дороге нужно провести шоссе с завода, чтобы доставка грузов из А в В была наиболее дешевой, если стоимость перевозки 1 тонны-километра по шоссе в два раза дороже, чем по железной дороге?
148. Расходы на топливо для парохода пропорциональны кубу его скорости. Известно, что при скорости 10 км/ч расходы на топливо составляют 30 руб/час, остальные расходы (не зависящие от скорости) составляют 480 руб/час. При какой скорости парохода общая сумма расходов на 1 км пути будет наименьшей? Какова будет при этом общая сумма расходов в час?
 Найдите интервалы выпуклости и точки перегиба функций:
Найдите интервалы выпуклости и точки перегиба функций:
149. 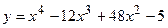 ;
;
150. 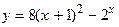 ;
;
151. 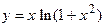 ;
;
152. 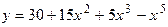 .
.
Найдите асимптоты графиков функций:
153. 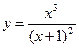 ;
;
154. 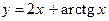 .
.
 Исследуйте функции и постройте их графики:
Исследуйте функции и постройте их графики:
155. 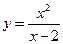 ;
;
156. 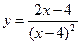 ;
;
157. 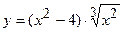 ;
;
158. 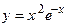 ;
;
159. 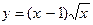 ;
;
160. 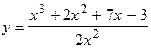 ;
;
161. 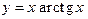 .
.
162. Функция 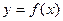 определена на отрезке [–4; 7]. На рисунке изображен график ее производной. Найдите точку минимума функции
определена на отрезке [–4; 7]. На рисунке изображен график ее производной. Найдите точку минимума функции 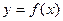 , промежуток убывания функции, угловой коэффициент касательной к графику функции в точке
, промежуток убывания функции, угловой коэффициент касательной к графику функции в точке 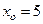 .
.
163. Функция 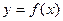 определена на отрезке [–4; 7]. На рисунке изображен график ее производной. Найдите точки максимума и минимума функции, промежуток убывания функции, угловой коэффициент касательной к графику функции в точке
определена на отрезке [–4; 7]. На рисунке изображен график ее производной. Найдите точки максимума и минимума функции, промежуток убывания функции, угловой коэффициент касательной к графику функции в точке 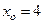 .
.








