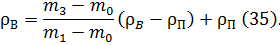Розділ іі. Експериментальні установки і теорія проведення дослідів.

Дата: 2025-04-30; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Більшість науковихдосліджень пов'язаних з експериментом. Він проводиться у лабораторіях, на виробництві, на дослідних полях та ділянках, в клініках і т.д.

Експеримент може бути фізичним, психологічним або модельним. Він може безпосередньо проводитись на об'єкті або на його моделі. Модель зазвичай відрізняється від об'єкта маштабом, а іноді природою.

Якщо модель досить точно описує об'єкт, то експеримент на об'єкті може бути замінений експериментом на моделі. Останнім часом поряд з фізичними моделями все більшого поширення набувають абстрактні математичні моделі.

Експеримент займає центральне місце в науці. Однак виникає питання, наскільки ефективно він використовується. Наукові дослідження організовуються і проводяться настільки хаотично, що їх коефіцієнт корисної дії може бути оцінений величиною порядку 2%. для того щоб підвищити ефективність досліджень, потрібно щось зовсім нове. Одним з можливих шляхів є застосування математичних методів, побудова математичної теорії планування експерименту.

Планування експерименту — це процедура вибору числа та цмов проведення дослідів, необхідних і достатніх для вирішення поставленого завдання з необхідною точністю.

При цьому істотно наступне:

l прагнення до мінімілізації загального числа дослідів;

l одночасне варіювання всіма змінними, які визначають процес, за спеціальними правилами — алгоритмами;

l використання математичного апарату, формалізує багато дій експериментатора;

l вибір чіткої стратегії, що дозволяє приймати обгрунтовані рішення після кожної серії експериментів.

Пошук оптимальних умов є однією з найбільш поширених науково-технічних завдань. Вони виникають в той момент, коли встановлена можливість проведення процесу і необхідно знайти найкращі (оптимальні в деякому розумінні) умови його реалізації.

Слід підкреслити, що завжди необхідно чітко формулювати, в якому сенсі умови повинні бути оптимальними. Цим визначається вибір мети дослідження. Точне формулювання мети значною мірою визначає успіх досліджеггя.

Планування експериментального експерименту — це метод вибору кількості та умов проведення дослідів, мінімально необхідних для відшукування оптимальних умов, тобто для вирішення поставленого завдання.

При цьому передбачається побудова фізичної моделі процесу на підставі ретельного вичення механізму явищ (наприклад, кінетики, гідродинаміки), що дозволяє отримати матиматичну модель об'єкта у вигляді системи диференціальних рівнянь.

Результати експерименту використовуються для отримання матиматичної моделі об'єкта дослідженя, яка являє собою рівняння, що зв'язує параметр оптимізації та фактори. Таке рівняння називається функцією відгуку.

Отже, щоб виробляти експеримент в найбільш короткий термін з найменими витратами, отримуючи при цьому достовірну інформацію, необхідно планування. Цого можна досягти, дотримуючись при плануванні певних правил, які враховують імовірнісний характер результатів вимірювань і наявність зовнішніх перешкод, що впливають на досліджуваний об'єкт.

При плануванні всі фактори, що визначають процес, змінюються одночасно за спеціальними правилами, а результати експерименту представляються у вигляді матиматичної моделі, що володіє деякими статистичними властивостями.

Виділяють наступні етапи планування:

l збір та аналіз інформації;

l вибір вхідних і вихідних змінних, обслатсі експериментування (зміни змінних);

l вибір матиматичної моделі, за допомогою якої будуть представлятися експериментальні дані;

l вибір критерію оптимальності та плану експерименту;

l визначення методу аналізу даних;

l проведення експерименту;

l перевірка статистичних передумов для отримання експериментальних даних;

l обробка результатів;

l інтерпритація та рекомендації.

В процесі огляду і аналізу інформації встановлюють і аналізують відомі дані по досліджуваному об'єкті: які фактори і як впливають на його стан, можливі межі зміни цих факторів, їх взаємозв'язок та ін.

Фактори можуть бути — кількісними і якісними. Рівням кількісних факторів відповідає числова шкала (температура, тиск і т.п.). якісні фактори — каталізатори, конструкції апаратів і т.п.

Вихідні змінні — реакції (відгуки) на вплив вхідних параметрів. Можуть бути економічними (витрата енергії, прибуток тощо), технологічними (стабільність горіння дуги, надійність і т.п.) і т.д.

Метрологічне забезпечення експерименту

вимірювання — процес знаходження якої фізичної величини дослідним шляхом за допомогою спеціальних технічних засобів. Це процес порівняння величини чого-небудь з відомою величиною, прийнятої за одиницю (еталон).

Вимірювання є основною складовою частиною будь-якого експерименту. Від їх старанності залежить результат експерименту.

Точність вимірювання — це ступінь наближення вимірювання до дійсного значення вимірюваної величини.

Похибка вимірювання — це алгебраїчна різниця між дійсним значенням вимірюваної величини і отриманим при вимірюванні.

Похибки при вимірюванні виникають унаслідок ряду причин: недосконалість методів і засобів вимірювань, недосконалість ретельного проведення досліду, впливу різних зовнішніх факторів, суб'єктивних особливовстей експериментатора та ін. Похибки бувають систематичними і випадковими.

Систематичні — такі похибки вимірювань, які при повторних дослідах залишаються постійними (або змінюються за відомим законом). Якщо чисельність значення цих похибок відомі, їх можна враховувати під час повторних вимірювань.

Випадкові — виникають чисто випадково при повторному вимірюванні. Їх не можна враховувати і виключити.

Засоби вимірів

Засоби вимірювань — сукупність технічних засобів, що використовуються при вимірюваннях і мають нормовані метрологічні характеристики. Вимірювальні засоби діляться на зразкові і технічні.

Зразкові — є еталонами і призначені для перевірки технічних (робочих) засобів.

Вимірювані прилади характеризуються величиною похибки і точності, стабільності вимірювань і чутливістю.

Похибка одна з найважливіших характеристик приладу. Розрізняють абсолютну і відносну похибку.

Точність — основна характеристика приладу. Характеризується сумарною похибкою. В залежності від допустимої похибки прилади діляться на класи. Часто клас точності позначають допустимою похибкою 4%.

Обробка результатів експерименту

На початку результати вимірювань зводять у таблиці, ретельно вивчають сумнівні дані, встановлюють причини їх різкиої відмінності від статистичного ряду спостережень, від середніх величин.

При аналізі величин необхідно встановити точність, з якою потрібно проводити обробку дослідних даних. Точність обробки не повинна бути вище точності вимірювань.

Графічне зображення результатів

При обробці результатів вимірювань широко використовують методи графічного зображення, які дають більш наочне уявлення про результати експерименту, ніж табличні дані. Для графічного зображення використовують зазвичай прямокутну систему координат.

Якщо при побудові графіка з'являються точки (одна — дві), які різко відділяються від плавної кривої, то необхідно проаналізвувати причину цього відхилення (груба помилка вимірювання або природний хід процесу), а також повторити вимірювання в діапазоні різкого відхилення точки. Повторні вимірювання підтвердять чи відкинути (в разі грубої помилки) наявність зазначеного відхилення. Якщо вимірювана величина є функцією двох змінних параметрів, то в одних координатах можна побудувати декілька графіків змінних параметрів, то в одних координатах можна побудувати декілька графіків, розбивши діапазон зміни одного з параметрів на кілька відрізків.

При побудові графіків велике значення має вибів масштабу. Масштаб по координатних осях зазвичай застосовують різний, шо дозволяє уникнути занадто вузьких (високих) або широких (низьких) графіків. Графіки з мінімумом або максимом необхідно особливо ретельно викреслювати в області екстемуму, тому тут експериментальні точки повинні бути частіше.

2.1. Метод Стокса.

Одним з широко використовуваних методів визначення коефіцієнта в’язкості є метод Стокса , який ґрунтується на вимірюванні швидкості рівномірного руху тіла сферичної форми (кульки) в досліджуваній рідині. Вираз для сили опору було встановлено емпіричним шляхом англійським фізиком та математиком Дж. Стоксом. Сила Стокса виникає завдяки тому, що під час руху кульки в рідині має місце тертя між окремими шарами рідини. Так, найближчий до поверхні кульки шар рідини матиме швидкість кульки, бо рідина немовби налипає на неї. Інші шари матимуть тим меншу швидкість, чим далі знаходяться від кульки.

На тіло, що повільно падає в рідині, діють (рис. 3):

(рис.3)

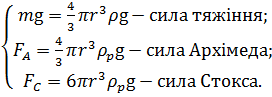(16)

Внаслідок зростання швидкості падіння кульки сила опору також зростатиме (див. формулу сили Стокса). Тоді настане такий момент, коли сила тяжіння зрівноважиться силами FС та FА, після чого кулька почне рухатись рівномірно:

mg = 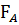+ 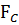(17).

З наведеної системи рівнянь та останнього рівняння можна одержати формулу для розрахунку коефіцієнта динамічної в’язкості рідини:

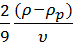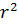η = g (18),

де r − густина матеріалу, з якого зроблена кулька; 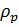− густина досліджуваної рідини; υ − швидкість рівномірного падіння кульки; g − прискорення вільного падіння; r − радіус кульки.

Вимірявши на досліді швидкість рівномірного падіння кульки в рідині, з останньої формули визначають коефіцієнт динамічної в’язкості рідини.

Застосування методу Стокса має свої обмеження:

а) може застосовуватись тільки тверда кулька, яка рухається рівномірно без обертання, при відсутності турбулентності (<1);

б) може застосовуватись, якщо рідина є гідродинамічно нестисливою, гомогенною і має необмежену протяжність у всіх напрямках, тобто радіус кульки не повинен перевищувати 1/10 радіуса циліндра, в якому знаходиться досліджувана рідина;

в) якщо досліджувані рідини прозорі.

З поправкою на вплив стінок циліндра швидкість кульки:

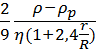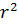υ = g (19),

де − радіус циліндра.

2.2. Метод Пуазейля.

Серед методів вимірювання коефіцієнта в’язкості рідини, особливо в’яжучих речовин, широкого поширення набув метод витікання рідини через капіляр. Цей метод має назву методу Пуазейля та ґрунтується на ламінарній течії рідини в тонкому капілярі для значного часу протікання (τ<100 с).

Розглянемо капіляр радіусом R та довжиною l. В рідині виділимо циліндричний шар радіусом r та товщиною dr (рис. 4). Сила внутрішнього тертя, яка діє на бічну поверхню цього шару:

(рис. 4)

F = -η 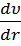dS = -η2πrl 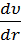(20),

де dS − бічна поверхня циліндричного шару, а знак мінус означає, що при збільшенні радіуса швидкість зменшується.

Для встановленої течії рідини сила внутрішнього тертя, яка діє на бічну поверхню циліндра, зрівноважується силою тиску, що діє на його основу ( 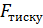=∆pS):

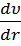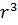-η2πrl = ∆pπ (21).

Звідси:

dυ = - 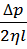rdr (22).

Після інтегрування, врахувавши, що біля стінок має місце притирання рідини, тобто швидкість на відстані від осі дорівнює нулю (рис. 4), одержимо:

υ = 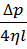( 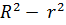) (23).

З останньої формули видно, що швидкість частинок рідини розподіляється за параболічним законом, причому вершина параболи лежить на осі труби (рис. 4). За час t з труби витікає рідина, об’єм V якої буде за законом Пуазейля:

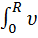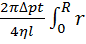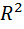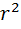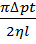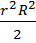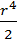
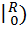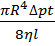V = t·r·dr = ( - )dr= ( - = (24),

де ∆p − різниця тисків на кінцях капіляра.

Звідки в’язкість:

η = 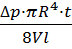(25).

Барр показав, що для певного радіуса капіляра існує критична швидкість витікання ( 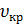), вище від якої течія рідини переходить у турбулентну. За Рейнольдсом:

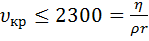(26).

Метод Пуазейля дуже спрощується, якщо вимірювати коефіцієнти в’язкості рідин відносним способом. При цьому досить виміряти час протікання однакового об’єму ( 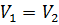) різних рідин через той самий капіляр та взяти відношення відповідних рівностей за законом Пуазейля:

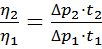(27).

Знаючи коефіцієнт в’язкості однієї рідини, визначаємо коефіцієнт в’язкості іншої рідини. Відношення тисків ∆ 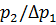визначають завдяки конструктивним особливостям приладу.

2.3. Капілярний метод дослідження в’язкості.

Прилади для вимірювання в’язкості рідин називаються віскозиметрами (від лат. viscosus – в’язкий та грец. metréõ – вимірюю). Найбільш розповсюдженими є капілярні, ротаційні, з рухомою кулькою та ультразвукові віскозиметри. Розглянемо один із них.

Віскозиметр Оствальда – Пінкевича являє собою -подібну скляну трубку (рис. 5). Одне коліно її має кулясте розширення 1, обмежене двома позначками для відліку об’єму досліджуваної рідини, і впаяний капіляр 2. Друге коліно з розширенням 3 призначене для зливання рідини, що протікає через капіляр. Спочатку в це коліно вливають вимірною піпеткою певний об’єм рідини (однаковий у дослідах з різними рідинами), а звідси за допомогою гумової груші 4 рідину засмоктують з розширення 1. Далі вимірюють час витікання цієї рідини через капіляр.

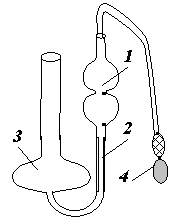(рис. 5).

Оскільки рідина витікає внаслідок різниці рівнів у колінах віскозиметра (ця різниця є однаковою в дослідах з різними рідинами), то замість відношення тисків (p =ρgh), під якими витікають рідини, можна взяти відношення їхньої густини :

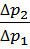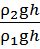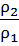= = (28).

Тоді формула для визначення коефіцієнта в’язкості рідин відносним методом за допомогою віскозиметра Оствальда – Пінкевича буде:

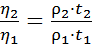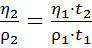, або (29),

тобто:

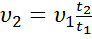(30),

де 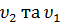та – коефіцієнти кінематичної в’язкості досліджуваної та відомої рідини, відповідно. Отже, капілярним віскозиметром Оствальда–Пінкевича безпосередньо вимірюють кінематичну в’язкість рідини. Щоб забезпечити сталу температуру в дослідах, віскозиметр вміщують у термостат або велику посудину з водою заданої температури, яка підтримується сталою на протязі всього досліду. Густину досліджуваної рідини визначають пікнометром .

2.4. В изначення густини пікнометричним способом .

Пікнометричний метод волюмометричного аналізу базується на визначенні об’єму рідини, яка витісняється із спеціальної посудини (пікнометра) при зануренні в нього зразка досліджуваного матеріалу. Пікнометричний метод є одним з точних методів (0,1 \%) визначення густини тіла, оснований на зважуванні та одному з основних законів гідростатики – законі Архімеда.

Пікнометр є скляною невеликою посудиною (своєрідною мірною колбою) певної ємності (для твердих тіл – 10; 25 і 50 см3; для рідин – 1; 2; 3; 5; 10; 50 і 100 см3) кулястої або циліндричної форми.

На рис. 6 показані найбільш розповсюджені типи пікнометрів. В пікнометрі першого типу (рис. 6, а) з глухою притертою кришкою рідина наливається піпеткою до мітки на шийці пікнометра. Через те, що при послідовному наповненні пікнометра об’єми досліджуваної рідини та рідини з відомою густиною (наприклад, дистильованою водою) є однаковими, а вагу рідин можна визначати з високою точністю на аналітичних терезах, то шукану густину також можна визначити досить точно. Другий вид пікнометра (рис. 6, б) має притерту пробку з капілярним отвором. Якщо пікнометр, який наповнено до країв рідиною, закрити пробкою, то надлишок рідини витісняється через капіляр. В результаті пікнометр буде наповнено до верхнього краю капіляра.

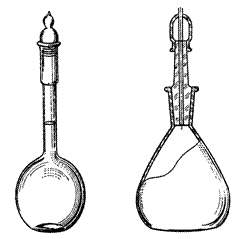а б (рис. 6)

Перед початком вимірювань необхідно з рідини видалити розчинене в ній повітря. Для цього рідину в стакані поміщають у спеціальну посудину, з якої відкачують повітря. Через деякий час з рідини починають виділятися бульбашки і вона звільняється від повітря. Після цього рідину дуже швидко переливають у пікнометр. При точних визначеннях густини температура рідини повинна залишатися строго постійною, чого можна досягти термостатуванням.

1. Щоб визначити густину твердого тіла пікнометричним методом, виконують три зважування:

· досліджуваного тіла в повітрі;

· пікнометра, наповненого дистильованою водою (або іншою допоміжною рідиною відомої густини), в повітрі;

· пікнометра, наповненого рідиною із зануреним у ньому твердим тілом, у повітрі.

Умови рівноваги терезів при цих зважуваннях з урахуванням дії сили Архімеда будуть такими:

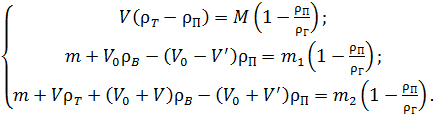(31)

де V– об’єм досліджуваного тіла; 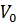– місткість пікнометра до мітки; 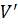– об’єм скла пікнометра; m – маса пустого пікнометра; M – маса гир, які зрівноважують тіло в повітрі; 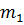– маси гир, що зрівноважують пікнометр з водою; 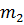– маси гир, що зрівноважують пікнометр з водою та зануреним у неї твердим тілом; 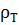– густина досліджуваного тіла; 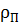– густина повітря; 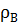– густина дистильованої води; 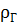– густина матеріалу, з якого виготовлено гирі.

Умова рівноваги для зважування порожнього пікнометра є такою:

m- 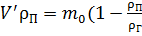) (32),

де 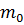– маса гир, які зрівноважують пустий пікнометр у повітрі.

Після деяких математичних перетворень формул (31) та (32) (надаємо можливість зробити це самостійно), дістанемо формулу для розрахунку густини твердого тіла при пікнометричному методі волюмометричного аналізу:

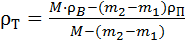(33).

2. Щоб визначити густину рідини пікнометричним методом також виконують три зважування:

1) порожнього пікнометра;

2) пікнометра, заповненого дистильованою водою до заданого рівня;

3) пікнометра, заповненого досліджуваною рідиною до того самого рівня.

Якщо позначити через 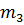масу гир, що зрівноважують пікнометр з досліджуваною рідиною, а через 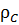та 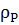– густини скла і досліджуваної рідини, відповідно, а інші позначення залишити такими самими, як і при дослідженні густини твердого тіла , умови рівноваги терезів з урахуванням дії сили Архімеда при цих зважуваннях відповідно до кроків зважування будуть такими:

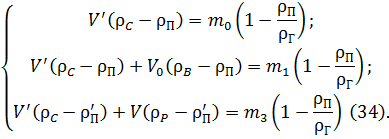
Розв’язуючи спільно рівняння (31), (32) та (34), можна отримати формулу для обчислення густини рідини при пікнометричному методі: