Розділ І. В’язкість і реологія. Основні поняття.
В’язкість
В'язкість або внутрішнє тертя — властивість рідких речовин (рідин і газів) чинити опір переміщенню однієї їх частини відносно іншої. Одиниця вимірювання динамічного коефіцієнта в'язкості — Пуаз.
Природа в'язкості
В’язкість рідин – це результат взаємодії внутрішньомолекулярних силових полів, що перешкоджають відносному рухові двох шарів рідини. Отже для переміщення шару один відносно одного треба подолати їх взаємне притягання, причому чим воно більше, тим більша потрібна сила зсуву. При відносному зсуві шарів у газовому середовищі, в результаті перенесення молекулами газу кількості руху під час їх переходу з шару в шар, виникає дотична сила між шарами, що протидіє проковзуванню останніх.
Таким чином, внутрішнє тертя в рідині, на відміну від газів, зумовлене не обміном молекул, а їх взаємним притяганням. Доказом цього є те, що із збільшенням температури, як відомо, обмін молекул зростає і тертя в газах зростає, а в рідинах спадає у зв'язку із послабленням міжмолекулярного притягання.
В'язкість твердих тіл має низку специфічних особливостей і зазвичай розглядається окремо.
Згідно із законом Ньютона для внутрішнього тертя в'язкість характеризується коефіцієнтом пропорційності η між напруженням зсуву T і градієнтом швидкості руху шарів 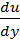 у перпендикулярному до деформації зсуву напрямку (поверхні шарів):
у перпендикулярному до деформації зсуву напрямку (поверхні шарів):
T = η 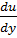 (1).
(1).
Коефіцієнт η називають динамічний коефіцієнт в’язкості або абсолютною в'язкістю. Одиниця вимірювання динамічного коефіцієнта в'язкості — Паc, Пуаз (0,1Па·с).
Кількісно динамічний коефіцієнт в'язкості дорівнює силі F, яку треба прикласти до одиниці площі зсувної поверхні шару S, щоб підтримати в цьому шарі ламінарну течію із сталою одиничною швидкістю відносного зсуву.
Типи в'язкості
Закон Ньютона для в'язкості, наведений вище, є класичною моделлю в'язкості. Це не основний закон природи, а наближення, що має місце для деяких матеріалів і не підтверджується для інших. Неньютонівські рідини мають значно складніший зв'язок між напруженням зсуву і градієнтом швидкості, ніж проста лінійність. Тому, для різних видів рідин застосовують різні моделі в'язкості:
· Ньютонівська рідина: рідина, така як вода і більшість газів, що має стале значення динамічної в'язкості.
· Дилатантна рідина: рідина, в'язкість якої із зростанням градієнту швидкості зростає (глиняні суспензії, солодкі суміші, гідрозоль кукурудзяного крохмалю, системи пісок/вода).
· Псевдопластик: рідина, в'язкість якої із зростанням градієнту швидкості зменшується (фарби, емульсії, деякі суспензії).
· Тиксотропна рідина: рідина, в'язкість якої з перебігом часу зменшується (водоносні ґрунти (пливуни), біологічні структури, різні технічні матеріали).
· Реопексна рідина: рідина, в'язкість якої з перебігом часу зростає (гіпсові пасти, суспензії оксиду ванадію, бетоніти та окремі види принтерного чорнила).
· Бінгамівський пластик: модель Бінгама схожа до моделі сухого тертя. В статичних умовах рідина веде себе як твердий матеріал, а при силовому впливі починає текти..
· Магнітореологічна рідина це тип "смарт-рідини", яка, при впливі магнітного поля значно збільшує свою умовну в'язкість і набуває властивостей в'язко-пружного твердого тіла.
Реологія
Реоло́гія (від грец. ρέω — течу і λογος — вчення) (рос. реология, англ. rheology, нім. Rheologie f) — наука про текучість і деформацію суцільних середовищ (наприклад, звичайних в'язких рідин і рідин аномальної в'язкості, гірських порід, суспензій, гідросумішей тощо).
Термін «реологія» ввів американський учений Юджин Бінгам, якому належать важливі дослідження реологій рідин і дисперсних систем. Офіційно термін «реологія» прийнятий на 3-му симпозіумі по пластичності (1929, США), однак, окремі положення реології як науки були встановлені задовго до цього.
Наукові основи реології
В основі реології лежать основні закони гідромеханіки та теорії пружності і пластичності (у т. ч. закон Ньютона для в'язкого тертя у рідинах, рівняння Нав'є-Стокса для руху нестисливої в'язкої рідини, закон Гука про опір деформуванню пружного тіла та ін.).
Реологія може розглядатися як частина механіки суцільних середовищ. Основне завдання реології — встановити залежність між механічними напруженнями, що виникають у тілі, і викликаними ними деформаціями та їх змінами в часі. За припущень про однорідність та суцільність матеріалу вирішують крайові задачі деформування та плину твердих і рідких тіл. Основна увага звертається на складну реологічну поведінку речовини (наприклад, коли одночасно виявляються властивості в'язкості і пружності або в'язкості та пластичності і т.д.).
Реологія охоплює коло питань, що знаходяться у проміжку між питаннями, які розглядає теорія пружності ідеально пружних тіл і питаннями механіки ньютонівських рідин і до яких відносяться задачі, пов'язані з деформацією і потоками реальних матеріалів, що зустрічаються на практиці — від розплавів металів до сильно розріджених рідин — таких, як, наприклад, піна. У таблиці 1 показано зв'язок між розділами класичної механіки та реологією рідин:
Таблиця 1
| Механіка суцільних середовищ: вивчення поведінки суцільних середовищ
| Механіка деформівного твердого тіла: вивчення поведінки твердих тіл в умовах навантажень. | Теорія пружності: описує матеріали, котрі відновлюють свою форму після припинення силового впливу на них. | |
| Механіка руйнування: описує закономірності зародження і розвитку неоднорідностей і дефектів структури матеріалу типу тріщин, дислокацій, пор, включень і т.п. при статичних і динамічних навантаженнях. | |||
| Теорія пластичності: описує матеріали (тіла) що набувають незворотної деформації після прикладання до них силових впливів. | Реологія: дослідження матеріалів, що характеризуються одночасно властивостями твердих тіл і рідин. | ||
| Механіка рідин та газів: дослідження поведінки суцільних середовищ (рідин та газів), що набувають форми посудини, у якій вони знаходяться. | Неньютонівські рідини | ||
| Ньютонівські рідини
| |||
Реологічні моделі
Напружено-деформований стан тіла в загальному випадку є тривимірним і описати його властивості з використанням простих моделей нереально. Однак у тих окремих випадках, коли деформування одновісне, якісно поведінку матеріалу наочно і просто можна змоделювати найпростішими структурними елементами. Реологічними моделями користуються також при вивченні механічних властивостей полімерів, внутрішнього тертя в твердих тілах і інших властивостей реальних тіл.
При описі реологічної поведінки матеріалів користуються механічними моделями, для яких записують диференціальні чи інтегральні рівняння, куди входять різні комбінації пружних, в'язких та пластичних характеристик. Основними є три елементи:
· пружний (гвинтова пружина) — пружне тіло Гука (H);
· в'язкий (гідравлічний амортизатор) — в'язка рідина Ньютона (N);
· пластичний (пластинка із сухим тертям на фрикційній підкладці) — жорсткопластичне тіло Сен-Венана (StV).
Закони деформування (зв'язок між механічним напруженням σ і відносною деформацією ε записуються лінійними рівняннями:
Н:ϭ = Еϵ — закон Гука;
N:ϭ = η 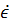 — закон Ньютона для внутрішнього тертя;
— закон Ньютона для внутрішнього тертя;
StV:ϭ = 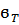 sgn
sgn 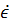 =
= 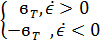 — модель границі текучості,
— модель границі текучості,
де: E — модуль Юнга; η — динамічна в'язкість; 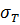 — границя текучості.
— границя текучості.
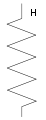
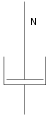
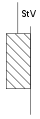
Пружне тіло Гука В’язке тіло Ньютона Тіло сухого тертя Сен-Венана
Мал.1
Крім того, співвідношення між напруженням і деформацією можна брати нелінійними.
З трьох основних елементів можна створювати комбінації з їх послідовним і паралельним сполученням. При послідовному сполученні двох елементів σ = σ1 = σ2, ε = ε1 + ε2. Для паралельного сполучення σ = σ1 + σ2, ε = ε1 = ε2.
До найвідоміших моделей слід віднести наступні:
· модель Кельвіна-Фойгта — модель твердого тіла, напруження у якому залежать від швидкості деформування;
· модель Максвелла — модель твердого тіла з властивостями текучості при довільному сталому навантаженні;
· модель Зінера (модель стандартного лінійного тіла) — реологічна модель лінійного в'язкопружного тіла, що складається з двох пружних елементів та в'язкого елемента, що узагальнює характеристики моделей Кельвіна-Фойгта та Максвелла;
· модель Прандтля — модель твердого тіла з пружними властивостями до певної межі навантаження, перевищення якої приводить до необмеженої миттєвої деформації;
· модель Бінгама — модель матеріалу властивості текучості якого проявляються після досягнення певної межі навантаження а опір деформуванню залежить від швидкості деформації.
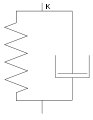
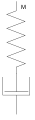
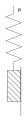
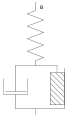
Модель Модель Модель Модель
Кельвіна-Фойгта Максвелла Прандтля Бінгама
Мал.2
Перелічені класичні моделі відбивають властивості матеріалів лише у певному наближенні, для повнішого охоплення властивостей будують моделі значно складнішої структури.
Прикладне значення
З проблемами реології доводиться зустрічатися при розробці технологій різних виробничих процесів, при проектних роботах і конструкторських розрахунках для врахування поведінки різних матеріалів (особливо при високих температурах): полімерів, композиційних матеріалів, бетонів, силікатів, харчових продуктів та ін.
Методи реології стали застосовуватися для цілей оперативного керування технологічними процесами. При цьому здійснюється безперервне або періодичне визначення однієї чи декількох реологічних властивостей сировини і (або) продукту за заданою програмою і з використанням зворотного зв'язку проводиться коригування до заданих меж параметрів сировини, процесу чи дозування вхідних інгредієнтів.
Методи реології використовують у металургійному та полімерному виробництві, гірничій справі, при гідравлічному транспортуванні та ін. галузях.
Експериментальна реологія
Експериментальна реологія (реометрія) визначає реологічні властивості речовин за допомогою спеціальних приладів і випробувальних машин. Мікрореологія досліджує деформації і течію в мікрооб'ємах, наприклад в об'ємах, сумірних з розмірами часток дисперсної фази в дисперсних системах або з розмірами атомів і молекул. Біореологія вивчає плин різноманітних біологічних рідин (наприклад, крові), деформації різних тканин (м'язів, кісток, кровоносних судин) організму. Вивчення взаємодії потоків з електричним та магнітним полями, що можуть впливати на потоки як активно, так і опосередковано шляхом Зміни реологічних властивостей речовин, становить предмет електрореології і магнітореології.
1.1. Теорія Бачинського.
В рідинах механізм внутрішнього тертя є дещо іншим. На різницю між явищем внутрішнього тертя в газах і в рідинах уперше звернув увагу О. Й. Бачинський, який вказав на те, що в газах коефіцієнт внутрішнього тертя може не залежати від густини лише доти, доки густина ще не є такою великою, щоб сили взаємодії між молекулами могли впливати на їх переміщення. Але в дуже густих газах, і тим більше в рідинах, відстані між молекулами вже є такими малими, що міжмолекулярні сили не можуть не протидіяти переміщенню молекул рідини зовнішньою силою. І ця протидія повинна бути тим більшою, чим ближче розташовані молекули одна до одної, тобто чим більшою є густина речовини. Через те, що молекули рідини більшу частину часу знаходяться біля положень рівноваги, маса рідини захоплює сусідні шари в основному за рахунок сил зчеплення. З підвищенням температури текучість рідини зростає, а в’язкість зменшується. При нагріванні рідина розширюється і збільшується її „вільний об’єм”V - b (де b– „граничний об’єм”, який є близьким до сталої в рівнянні Ван дер Ваальса, яка характеризує недоступну для молекул частку повного об’єму системи V). Враховуючи це, О. І. Бачинський запропонував в 1912 р. дуже просту формулу, яка описує залежність в’язкості рідини від температури:
 (2),
(2),
де B – константа, різна для різних рідин.
Бачинський знайшов, що для багатьох рідин b дорівнює близько 0,3 від критичного об’єму 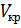 .
.
Із роботи Бачинського випливає, що чим більший питомий об’єм рідини, тим меншою буде в’язкість. Але з підвищенням температури питомий об’єм зростає, в наслідок чого в’язкість буде зменшуватись. Отже, як бачимо, формула Бачинського повністю відповідає експериментові.
Аналіз роботи Бачинського приводить до висновку, що V не може бути меншим від b, тобто b являє собою не що інше, як граничний об’єм рідини. Отже, різниця V - b - вільний об’єм. Згідно з Бачинським, b - це деяка проміжна величина між питомим об’ємом рідини і твердого тіла при температурі тверднення, тобто 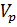 > b >
> b > 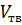 .
.
Тепер рівняння О.І. Бачинського вже добре обґрунтовано. Його теоретичному обґрунтуванню присвячено багато праць, серед яких назвемо роботи О.С. Предводителєва.
1.2. Теорія Френкеля.
У 1925 році Френкель розвинув свою молекулярно-кінетичну теорію в’язкості рідин. Більш ранні спроби пояснення в’язкості рідин виходили із загальноприйнятої на той час аналогії між рідким і газоподібним станом і зводили походження в’язкості до одного і того ж механізму перенесення кількості руху при змішуванні частинок. У випадку газів цей механізм виправдовується тим, що більшу частину часу частинки рухаються прямолінійно і рівномірно, так що кількість руху кожної з них залишається сталою. За таких умов ліквідацію відмінності у макроскопічному русі сусідніх шарів (чи елементів об’єму) можна трактувати як результат змішування молекул з різними додатковими (макроскопічними) швидкостями.
Запишемо формулу
η = А 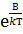 = А
= А 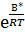 , (3)
, (3)
де А і В - деякі сталі, Т - термодинамічна температура, R - універсальна газова стала, 𝑘 - стала Больцмана
B = 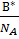 ,
, 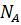 - число Авогадро.
- число Авогадро.
Ця формула, як і розвиток теорії в’язкості рідин, пов’язані з роботами Арреніуса, який вперше і запропонував для опису температурної залежності в’язкості схожий емпіричний вираз. Хоча, варто зазначити, що у своїх працях Арреніус привів більш загальну формулу
η= A 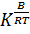 (4),
(4),
де K - деяка стала.
У 1925 р. Я.І. Френкель на основі молекулярно-кінетичних уявлень пропонує об’єднати такі, здавалося б, на перший погляд взаємовиключні властивості тіл, як текучість і твердість. На основі цих уявлень Френкель теоретично отримує і формулу Арреніуса. Результати його роботи детально представлені в монографії “Кінетична теорія рідин”, яка вперше вийшла у 1945 р. Практично одночасно аналогічні роботи з’явилися і за кордоном, найбільш детально розробленою можна вважати теорію Ейрінга, названу ним “Теорією абсолютних швидкостей реакції” (1946). Теорія рідин Френкеля відразу отримала велику популярність і визнання і значною мірою стимулювала розвиток фізики рідин (конденсованого стану).
Трактувати в’язкість рідини як результат переносу у ній кількості руху є абсолютно безглуздим, бо кількість руху кожної окремої частинки не є сталою навіть приблизно, як у випадку газів, але швидко коливається у зв’язку з коливаннями частинки навколо положення рівноваги. За таких умов можна виходити безпосередньо із рухливості окремих частинок, тобто середньої швидкості, яка набувається будь-якою з них відносно оточуючих, коли на неї діє сила, що дорівнює одиниці, у той час як оточуючі частинки не відчувають дії якихось зовнішніх сил. Очевидно, що текучість рідини, вимірювана величиною, оберненою до коефіцієнта в’язкості, повинна бути пропорційна рухливості частинок, що її утворюють. А так як остання, згідно з співвідношенням Ейнштейна, в свою чергу пропорційна до коефіцієнта дифузії, звідки слідує, що в’язкість рідин у твердоподібному стані (тобто поблизу температури тверднення), на противагу в’язкості газів, повинна бути не прямо пропорційна до коефіцієнта дифузії, а навпаки, обернено пропорційна до нього. Цією обставиною відразу ж пояснюється той факт, що з підвищенням температури в’язкість рідин зменшується. Так як коефіцієнт дифузії (самодифузії) рідин пропорційний до виразу 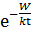 , то цим же виразом повинна визначатися і текучість рідин. Іншими словами, їх в’язкість, як функція температури, повинна визначатися формулою вигляду
, то цим же виразом повинна визначатися і текучість рідин. Іншими словами, їх в’язкість, як функція температури, повинна визначатися формулою вигляду
η = A 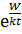 (5),
(5),
де коефіцієнт A можна вважати приблизно сталим.
1.3. Теорія Андраде.
У деяких джерелах формулу η = А 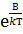 = А
= А 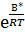 називають формулою Андраде. Андраде припускав, що передача руху від шару до шару рідини, що тече, здійснюється не шляхом перестрибування молекул, як у газів, а внаслідок тимчасового з’єднання їх на межі шарів. У кінцевому вигляді формула Андраде може бути записана у вигляді
називають формулою Андраде. Андраде припускав, що передача руху від шару до шару рідини, що тече, здійснюється не шляхом перестрибування молекул, як у газів, а внаслідок тимчасового з’єднання їх на межі шарів. У кінцевому вигляді формула Андраде може бути записана у вигляді
η 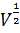 = A
= A 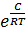 (6)
(6)
або
η = A 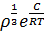 (7),
(7),
де А - стала, пропорційна до частоти коливань молекул;
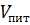 - питомий об’єм;
- питомий об’єм;
ρ = 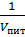 - густина.
- густина.
Взаємодія між молекулами окремих шарів здійснюється тільки з допомогою нормальних сил між ними; сили, тангенціальні до поверхонь агрегатів, відсутні.
Сама передача кількості руху може відбуватися тільки при сприятливій ситуації оточуючих частинок, тобто при певних значеннях їх потенційної енергії.
1.4. Теорія вільного об’єму.
Серед кінетичних теорій склування, заснованих на введенні єдиного внутрішнього параметра ξ, однією з найбільш розроблених і відомих є теорія вільного об'єму.
Передбачається, що кінетична поведінка системи визначається флуктуаціонним вільним об'ємом. Загальний вид формули для кінетичних коефіцієнтів:
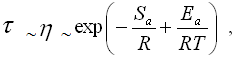 (8),
(8),
де Sa і Еа - ентропія і енергія активації процесів релаксації або в'язкої течії.
В загальному випадку вираз для 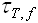 , у відповідності з теорією вільного об'єму має вигляд:
, у відповідності з теорією вільного об'єму має вигляд:
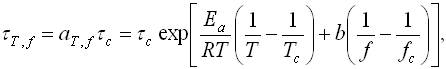 (9),
(9),
де f = Vf / Vd - частка флуктационного вільного об'єму.
Якщо виділити в f член, що залежить тільки від температури, і нерівноважний член, то одержимо:
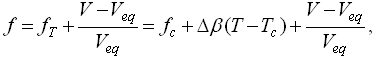 (10),
(10),
де Δ = (βж - βтв) - різниця ТКОР для переохолодженої рідини і скла при Тс.
Тоді на підставі:
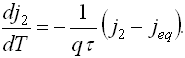 (11)
(11)
можна отримати рішення релаксаційного рівняння типу у вигляді:
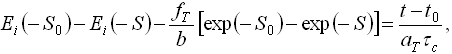 (12)
(12)
де
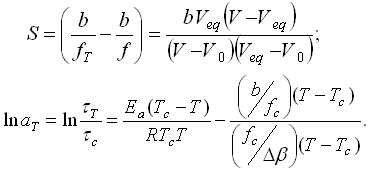 (13)
(13)
Залежність (12), що описує ізотермічну релаксацію обсягу, відрізняється від відповідних рівнянь теорії фіктивної температури і теорії Готліба - Птіцина членом
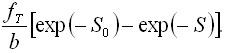 (14).
(14).
Наявність цього члена робить формулу (5) більш точної ніж :
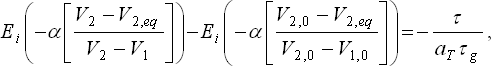 (15),
(15),
при великих відхиленнях системи від рівноваги. Таким чином, теорія вільного об'єму задовільно описує нелінійність і асиметрію релаксації вільного об'єму системи в області примусу, але, як і всі інші однопараметричні теорії, не в змозі описати залежність об'єму полімеру від температурно-часової передісторії.








