Глава 2 расчет вероятности получения положительной отметки при написании тестовой контрольной работы
2.1 Основы расчета вероятности получения положительной отметки
Основным понятием теории вероятностей является вероятность. Это слово достаточно часто применяется в повседневной жизни. Думаю, каждому знакомы фразы: «Завтра, вероятно, выпадет снег», или «вероятнее всего в выходные я поеду на природу». В словаре С.И.Ожегова дается толкование слова вероятность как «возможности осуществления чего-нибудь». И здесь же дается определение понятию теории вероятностей как «разделу математики, изучающей закономерности, основанные на взаимодействии большого числа случайных явлений».
При изучении явлений, мы проводим эксперименты, в ходе которых происходят различные события, среди которых различают: достоверные, случайные, невозможные, равновероятные.
Событие U называют достоверным по отношению к некоторому испытанию, если в ходе этого испытания событие U обязательно произойдет. Например, достоверным будет появление одного из шести чисел 1,2,3,4,5,6 при одном бросании игральной кости.
Событие называют случайным по отношению к некоторому испытанию, если в ходе этого испытания оно может произойти, а может и не произойти. Например, при однократном бросании игральной кости может выпасть число 1 или не выпасть, т.е. событие является случайным, потому что оно может произойти, а может и не произойти.
Событие V называют невозможным по отношению к некоторому испытанию, если в ходе этого испытания событие V не произойдет. Например, невозможным является выпадение числа 7 при бросании игрального кубика.
Равновероятные события – это события, которые при данных условиях имеют одинаковые шансы для наступления.
А как подсчитать вероятность случайного события? Ведь если случайное, значит, не подчиняется закономерностям, алгоритмам. Оказывается, и в мире случайного действуют определенные законы, позволяющие вычислять вероятности.
Принято вероятность события А обозначать буквой Р(А), тогда формула для вычисления вероятности записывается так:
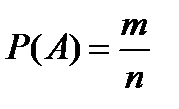, где 
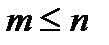(1)
Вероятностью Р(А) события А в испытании с равновозможными элементарными исходами называется отношение числа исходов m, благоприятствующих событию А, к числу исходов n всех исходов испытания. Из формулы (1) следует, что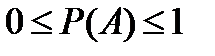 
.
Данное определение принято называть классическим определением вероятности. В настоящее время теория вероятностей нашла свое применение во многих вопросах науки, техники и человеческой деятельности.
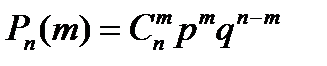При решении вероятностных задач часто приходиться сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент называется схемой повторных независимых испытаний или схемой Бернулли. Данная схема названа в честь выдающегося швейцарского математика Якоба Бернулли, выведшего формулу:
Пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытания независимы; вероятность появления события A в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события A в единичном испытании буквой p, то есть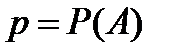 
, а вероятность противоположного события (событие А не наступило) - буквой 
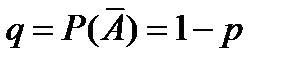Тогда вероятность того, что событие А появится в этих n испытаниях ровно m раз, выражается формулой Бернулли.
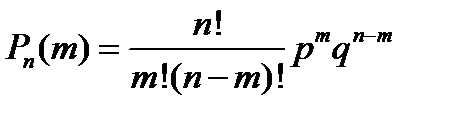
Определить вероятность получения положительной отметки за тестовую контрольную работу можно по формуле Бернулли.
2.2 Исследование и его результаты
Для подтверждения гипотезы исследования в 7 и 9 классах на уроках алгебры и геометрии были проведены контрольные работы в тестовой форме. Учащимся было предложено наугад выбрать правильный ответ или вписать его самостоятельно. В курсе математики мы изучали элементы теории вероятности, основные понятия и приемы обработки данных. Для решения данной проблемы нам понадобилось изучить дополнительную литературу, мы познакомились с историей развития теории вероятности и подобрали для обработки результатов повторных независимых испытаний формулу Бернулли, применяя данную формулу, мы вычислили вероятность получения положительной отметки при написании тестовой контрольной работы путем угадывания правильного ответа.
В начале исследования мы опросили всех учащихся школы, возможно ли набрать минимальное количество баллов для сдачи ОГЭ по математике. Результаты опроса приведены на диаграмме.
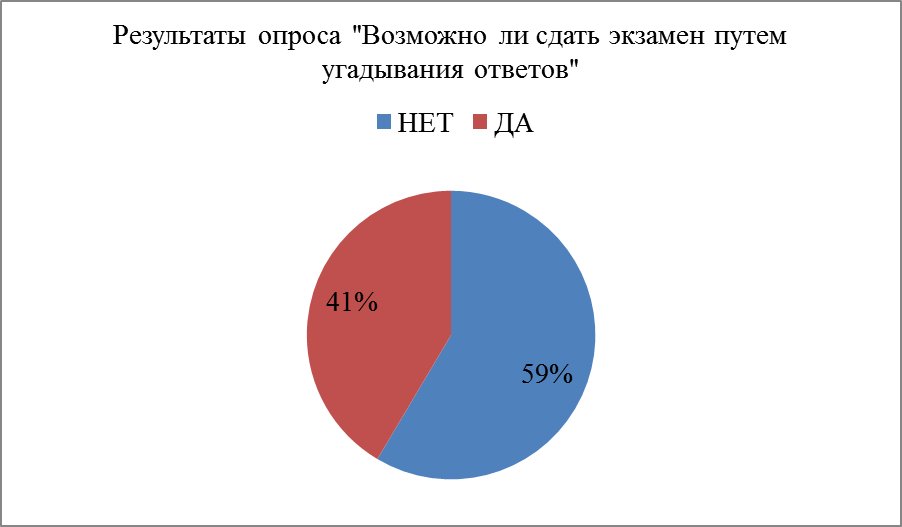
После этого учащимся была предложена контрольные работы по алгебре и геометрии. Контрольная работа по алгебре состояла из 15 заданий аналогичных экзаменационным.
Для того чтобы получить положительную отметку за контрольную работу по алгебре достаточно было угадать 8 правильных ответов.
Пусть событие А – это правильно выбранный ответ из четырех предложенных в одном задании. Вероятность события А определена как отношение числа случаев, благоприятствующих этому событию (то есть правильно угаданный ответ. Тогда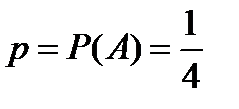 
.
Вероятность противоположного события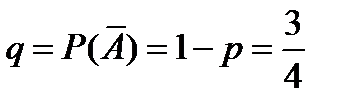 
.
Вероятность получения положительной отметки вычислим по формуле Бернулли, где n = 10, m = 8.
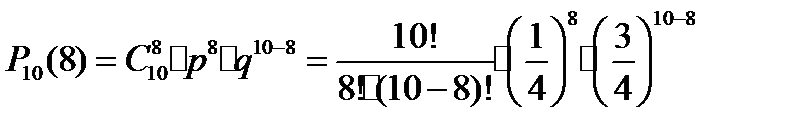
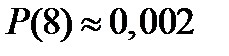
Таким образом, максимальное количество правильно угаданных ответов равно 4, что не позволяет ученику получить положительную отметку за контрольную работу по алгебре. Это же подтверждают теоретические вычисления – вероятность угадывания правильных ответов – достаточно мала, в данном случае только 0,002.
Контрольная работа по геометрии состояла из 5 заданий. Каждое задание имело 4 варианта ответа, один из которых правильный. Для того чтобы получить положительную отметку за контрольную работу по геометрии достаточно было угадать 3 правильных ответов.
Вероятность получения положительной оценки вычислим по формуле Бернулли, где n = 5, m = 3
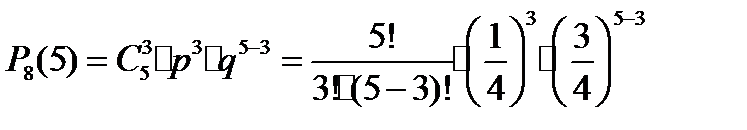
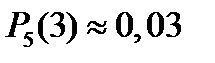
Таким образом, максимальное количество правильно угаданных ответов в контрольной работе по геометрии равно 3, что позволяет ученику получить положительной отметки. Это же подтверждают теоретические вычисления – вероятность угадывания правильных ответов – достаточно мала, в данном случае равна 0,03.
Таким образом, результаты практических экспериментов и их теоретическое обоснование говорят нам о том, что нельзя набрать минимальное количество баллов при сдаче ОГЭ, не зная материал курса математики.
ЗАКЛЮЧЕНИЕ
В результате проделанной работы, были решены поставленные задачи:
1. Изучили историю возникновения и применения теории вероятности в различных областях. «Теория вероятностей» - это огромный раздел науки математики.
2. Проведено анкетирование среди учащихся школы по вопросу «Можно ли сдать экзамен без подготовки, угадывая ответ в заданиях первой части». 59 % учащихся уверены в том, что без необходимых знаний невозможно положительно сдать экзамен.
3. Проведен эксперимент среди учащихся 7 и 9 классов по решению экзаменационных работ по математике. Учащиеся выполнили контрольные работы, опираясь лишь на тот багаж знания, которыми владели на момент эксперимента. Таким образом учащимся 7 класса приходилось записывать ответ путем угадывания.
4. Проанализированы результаты решения контрольных работ по математике в 7 и 9 классах. Исходя из полученных данных, был сделан вывод, что нельзя угадывая ответы преодолеть порог по математике, если отсутствуют знания по какой-либо теме.
С результатами данного исследования можно ознакомить будущих выпускников во время проведения классных часов, внеклассных мероприятий, с целью пропаганды подготовки их к экзаменам.
Таким образом, ранее выдвинутая гипотеза нашла свое подтверждение в проведенном исследовании.
БИБЛИОГРАФИЯ
1. Балдин, К.В., Башлыков, В.Н. Основы теории вероятностей и математической статистики: Учебник / К.В. Балдин, В.Н. Башлыков, А.В. Рукосуев. - М.: Флинта: МПСИ, 2010. - 488 с.
2. Лоэв, М. Теория вероятностей / М. Лоэв. - М.: ИЛ, 2012. – 718 с.
3. Минаева, С.С. Справочник по математике. Алгебра, геометрия. 7-9 классы / С.С. Минаева. – М.: Экзамен, 2019. – 176 с.
4. Митропольский, А.К. Техника статистических вычислений / А.К. Митропольский. - М.: Наука, 2006. – 576 с.
5. Кибзун, А.И., Горяинова, Е.Р. Теория вероятностей и математическая статистика. базовый курс с примерами и задачами. / А.И.Кибзун, Е.Р.Горяинова, А.В.Наумов, А.Н.Сиротин. - М.: Физматлит, 2002. - 224 с.
6. Рыжик, В.И. Геометрия. 7-9 классы. Диагностические тесты / В.И. Рыжик. - М., 2014. -174 с.
7. http://ru.wikipedia.org/
8. http://fipi.ru/
9. https://sdamgia.ru/
ПРИЛОЖЕНИЯ
Приложение 1