Глава 1. Теоретические аспекты формирование понятийного аппарата «теория вероятности»
Муниципальное казенное общеобразовательное учреждение
«Троицкая средняя общеобразовательная школа»
Кореневского района Курской области
Индивидуальный проект по математике
на тему:
«Вероятность получения положительной отметки при написании тестовой контрольной работы путем угадывания правильного ответа»
Выполнила:
Бородина Елизавета,
ученица 9 класса
Научный руководитель: Боряк Е.А.,
учитель математики
с. Троицкое, 2020
Оглавление
ВВЕДЕНИЕ. 3
ГЛАВА 1. ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ФОРМИРОВАНИЕ ПОНЯТИЙНОГО АППАРАТА «ТЕОРИЯ ВЕРОЯТНОСТИ». 5
1.1 Из истории становления теории вероятности. 5
1.2 История применения методов теории вероятности в различных областях 8
ГЛАВА 2 РАСЧЕТ ВЕРОЯТНОСТИ ПОЛУЧЕНИЯ ПОЛОЖИТЕЛЬНОЙ ОТМЕТКИ ПРИ НАПИСАНИИ ТЕСТОВОЙ КОНТРОЛЬНОЙ РАБОТЫ.. 11
2.1 Основы расчета вероятности получения положительной отметки. 11
2.2 Исследование и его результаты.. 13
ЗАКЛЮЧЕНИЕ. 16
БИБЛИОГРАФИЯ.. 17
ПРИЛОЖЕНИЯ.. 18
ВВЕДЕНИЕ
Мы не раз слышали или сами говорили “это возможно”, “это не возможно”, “это обязательно случится”, “это маловероятно”. Такие выражения обычно употребляют, когда говорят о возможности наступления события, которое в одних и тех же условиях может произойти, а может и не произойти.
Актуальность. Случай, случайность – с ними мы встречаемся повседневно. Кажется, как можно «предвидеть» наступление случайного события? Ведь оно может произойти, а может и не сбыться. Но математика нашла способы оценивать вероятность наступления случайных событий. Серьёзный шаг в жизни каждого выпускника 9 класса – ОГЭ. Успешная его сдача - это дело случая или нет?
Объект исследования: процесс выполнения заданий экзаменационных тестов путем угадывания правильного ответа.
Предмет исследования: метод обработки статистических данных по выбору правильного ответа при решении заданий из ОГЭ с помощью теории вероятности.
Цель исследования : определение вероятности успешной сдачи экзамена обучающимися 9 класса путем угадывания правильного ответа, применяя теорию вероятностей.
Гипотеза данного исследования заключается в том, что если учащиеся 7 класса смогут угадать больше верных ответов при решении заданий из первой части ОГЭ в отличие от учащихся 9 класса, то можно сказать о том, что есть вероятность получения положительной отметки, даже не имея достаточных знаний по предмету.
В соответствии с целью и гипотезой необходимо решить следующие основные задачи исследования:
1) изучить историю возникновения и применения теории вероятности в различных областях;
2) провести анкетирование среди учащихся 9 класса по вопросу: «Можно ли сдать экзамены без подготовки, угадывая ответ в заданиях первой части»;
3) провести статистический эксперимент по решению экзаменационных тестовых работ по математике в 7 и 9 классах;
4) проанализировать результаты решения экзаменационных тестовых работ средствами теории вероятности.
Методы исследования : анализ, сбор информации, эксперимент, анкетирование.
ГЛАВА 1. ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ФОРМИРОВАНИЕ ПОНЯТИЙНОГО АППАРАТА «ТЕОРИЯ ВЕРОЯТНОСТИ»
1.1 Из истории становления теории вероятности
Развитие теории вероятностей с момента зарождения этой науки и до настоящего времени было несколько своеобразным. На первом этапе истории этой науки она рассматривалась как занимательный «пустячок», как собрание курьезных задач, связанных в первую очередь с азартными играми в кости и карты, для переписи населения, и даже определения численности войска неприятеля.
В этот период, начало которого теряется в веках, ставились и решались элементарные задачи, которые позже будут отнесены к теории вероятностей. Никаких специальных методов в этот период не возникает. Этот период кончается работами Кардано, Пачоли и Тарталья.
С вероятностными представлениями мы встречаемся еще в античности. У Демокрита, Лукреция Кара и других античных ученых мы находим глубокое предвидение о строении материи с беспорядочным движением мелких частиц, мы встречаем рассуждения о равновозможных исходах.
К середине, XVII века вероятностные вопросы и проблемы, возникающие в статистической практике, в практике страховых обществ, при обработке результатов наблюдений и в других областях, привлекли внимание ученых, так как они стали актуальными вопросами.
В первую очередь это относится к Б. Паскалю, П. Ферма и X. Гюйгенсу. В этот период вырабатываются первые специфические понятия, такие, как математическое ожидание и вероятность (в форме отношения шансов), устанавливаются и используются первые свойства вероятности: теоремы сложения и умножения вероятностей. В это время теория вероятностей находит свои первые применения в демографии, страховом деле, в оценке ошибок наблюдения, широко используя при этом понятие вероятности.
Основателями теории вероятностей были французские математики Б. Паскаль и П. Ферма, и голландский ученый Х. Гюйгенс, давший самую раннюю из известных научных трактовок вероятности. По существу Гюйгенс уже оперировал понятием математического ожидания. Швейцарский математик Я. Бернулли, установил закон больших чисел для схемы независимых испытаний с двумя исходами.
Теория вероятностей как наука начинается с работы Якоба Бернулли (1654–1705) «Искусство предположений», опубликованной в 1716 году. В этом произведении уже введено и широко использовано понятие вероятности случайного события, доказаны некоторые общие теоремы и сделаны полезные примечания к работе Х. Гюйгенса.
Книга Я. Бернулли состоит из четырёх частей. Первая ее часть посвящена изложению работы Х. Гюйгенса и примечаниям к её содержанию.
Эти примечания, как правило, имеют большой самостоятельный интерес.
В частности в одном из них установлена известная формула Я. Бернулли для вероятности того, что при n независимых испытаниях событие А появится m раз с вероятностью, равной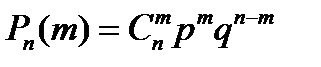 
, если в каждом из испытаний событие А наступает с вероятностью p и не наступает с вероятностью q = 1-p.
К этому периоду, который продолжался до середины XIX в., относятся работы Муавра, Лапласа, Гаусса и др. В центре внимания в это время стоят предельные теоремы. Теория вероятностей начинает широко применяться в различных областях естествознания. И хотя в этот период начинают применяться различные понятия вероятности (геометрическая вероятность, статистическая вероятность), господствующее положение занимает, в особенности после работ Лапласа, так называемое классическое определение вероятности.
Следующий период развития теории вероятностей связан прежде всего с Петербургской математической школой. За два столетия развития теории вероятностей главными ее достижениями были предельные теоремы. Но не были выяснены границы их применимости и возможности дальнейшего обобщения. Наряду с огромными успехами, достигнутыми теорией вероятностей в предыдущий период, были выявлены и существенные недостатки в ее обосновании, это в большой мере относится к недостаточно четким представлениям о вероятности.
Современный период развития теории вероятностей начался с установления аксиоматики. Этого прежде всего требовала практика, так как для успешного применения теории вероятностей в физике, биологии и других областях науки, а также в технике и военном деле необходимо было уточнить и привести в стройную систему ее основные понятия. Благодаря аксиоматике теория вероятностей стала абстрактно-дедуктивной математической дисциплиной, тесно связанной с другими математическими дисциплинами. Это обусловило небывалую широту исследований по теории вероятностей и ее применениям, начиная от хозяйственно-прикладных вопросов и кончая самыми тонкими теоретическими вопросами теории информации и теории случайных процессов.
Строгое логическое обоснование теории вероятностей произошло в XX в. и связано с именами советских математиков С.Н. Бернштейна и А.Н. Колмогорова.
Попыток изменить ситуацию и поставить теорию вероятностей на заслуженное место было много, однако лишь в 1933 году Колмогорову удалось это сделать. Его заслуга не только в том, что он внес полную ясность в формальное строение теории вероятностей, но и в том, что сделал это с минимальными изменениями. Ученый сумел применить уже готовый мощный инструмент — так называемую теорию меры. Однако все равно это оказалось делом нелегким. Историю открытия теории вероятностей можно сравнить с открытием Эйнштейном теории относительности.
Такой же луч света пролил и Колмогоров на всю пирамиду фактического и теоретического материала, собранного по теории вероятностей. До него все классические, статистические данные, философские мысли и теории для азартных игр были лишь «интуитивными предпосылками», «кирпичиками» современной теории вероятностей. Ученый наделил теорию всеми необходимыми элементами, чтобы ее можно было назвать математической дисциплиной. Ученый дал изучаемым объектам и их основным отношениям названия, а также заложил фундамент в виде аксиом, почти как в алгебре или геометрии. Аксиомы зафиксировали постулаты и правила, а выводы стали возможными исходя из установленных теорем.
С помощью развитых Колмогоровым методов появилась возможность решать самые разнообразные прикладные задачи. Исследования эти выполнялись в самых разных областях самим Андреем Николаевичем и его последователями. Одной из таких работ стало дополнительное подтверждение знаменитого генетического закона Менделя.
1.2 История применения методов теории вероятности в различных областях
Вплоть до конца 18 столетия прикладная статистика, без которой немыслим государственный учет и контроль, и потому существовавшая издавна, носила элементарный, чисто арифметический характер. Теория вероятностей оставалась чисто академической дисциплиной, и в качестве сравнительно сложных ее “приложений” выступали лишь азартные игры. Улучшение технологии производства игральных костей в 18 веке стимулировало развитие теории вероятности. Игроки, сами того не желая, начали в массовом порядке ставить воспроизводимые опыты, так как кости стали одинаковыми, стандартными. Так возник пример того, что впоследствии будет названо “статистическим экспериментом” - опыт, который можно повторять неограниченное число раз в одинаковых условиях.
В 19 и 20 столетиях теория вероятностей проникает сперва в науку (астрономию, физику, биологию), потом в практику (сельское хозяйство, промышленность, медицину), и наконец, после изобретения компьютеров, в повседневную жизнь любого человека, пользующегося современными средствами получения и передачи информации. Проследим основные этапы.
1. Астрономия. Именно для использования в астрономии был разработан знаменитый “метод наименьших квадратов” (Лежандр 1805, Гаусс 1815). Главной задачей, для решения которой он был первоначально использован, стал расчет орбит комет, который приходилось производить по малому числу наблюдений. Ясно, что надежное определение типа орбиты (эллипс или гипербола) и точный расчет ее параметров оказывается трудным, так как орбита наблюдается лишь на небольшом участке. Метод оказался эффективным, универсальным, и вызвал бурные споры о приоритете. Его стали использовать в геодезии и картографии. Сейчас, когда искусство ручных расчетов утрачено, трудно представить, что при составлении карт мирового океана в 1880-х годах в Англии методом наименьших квадратов была численно решена система, состоящая из примерно 6000 уравнений с несколькими сотнями неизвестных.
2. Физика. Во второй половине 19 века была в работах Максвелла, Больцмана и Гиббса была развита статистическая механика, которая описывала состояние разряженных систем, содержащих огромное число частиц (порядка числа Авогадро). Если раньше понятие распределения случайной величины было преимущественно связано с распределением ошибок измерения, то теперь распределенными оказались самые разные величины – скорости, энергии, длины свободного пробега.
3. Биометрия. В 1870-1900 годах бельгиец Кетле и англичане Френсис Гальтон и Карл Пирсон основали новое научное направление – биометрию, в которой впервые стала систематически и количественно изучаться неопределенная изменчивость живых организмов и наследование количественных признаков. В научный оборот были введены новые понятия – регрессии и корреляции.
Итак, вплоть до начала 20 века основные приложения теории вероятности были связаны с научными исследованиями. Внедрение в практику – сельское хозяйство, промышленность, медицину произошло в 20 веке.
4. Сельское хозяйство. В начале 20 века в Англии была поставлена задача количественного сравнения эффективности различных методов ведения сельского хозяйства. Для решения этой задачи была развита теория планирования экспериментов, дисперсионный анализ. Основная заслуга в развитии этого уже чисто практического использования статистики принадлежит сэру Рональду Фишеру, астроному(!) по образованию, а в дальнейшем фермеру, статистику, генетику, президенту английского Королевского общества. Современная математическая статистика, пригодная для широкого применения в практике, была развита в Англии (Карл Пирсон, Стьюдент, Фишер). Стьюдент впервые решил задачу оценки неизвестного параметра распределения без использования байесовского подхода.
5. Промышленность. Введение методов статистического контроля на производстве (контрольные карты Шухарта). Сокращение необходимого количества испытаний качества продукции. Математические методы оказываются уже настолько важными, что их стали засекречивать. Так книга с описанием новой методики, позволявшей сократить количество испытаний (“Последовательный анализ” Вальда), была издана только после окончания второй мировой войны в 1947 году.
7.Биоинформатика. Начиная с 1980-х годов количество известных последовательностей белков и нуклеиновых кислот стремительно возрастает. Объем накопленной информации таков, что только компьютерный анализ этих данных может решать задачи по извлечению информации.