Представление цифровых данны
Санкт-Петербургский
Государственный университет аэрокосмического приборостроения
А.А.Ключарёв , О.В.Мишура, С.Г.Марковский
ПРЕДСТАВЛЕНИЕ ЦИФРОВЫХ ДАННЫ
В ЦВМ
Учебно-практическое пособие
Санкт-Петербург
1999
С о с т а в и т е л и: к.т.н., доцент А.А Ключарёв.
к.т.н., доцент О.В Мишура.
старший преподаватель С.Г Марковский.
Р е ц е н з е н т: кафедра менеджмента науки и образования СПб.ГУАП ;
к.т.н., доцент А.Г.Степанов
В пособии рассматриваются способы представления информации в цифровых вычислительных машинах, позиционные системы, основы машинной арифметики. Изложение материала сопровождается примерами. Включённые в пособие методические материалы по выполнению соответствующей лабораторной работы и пример её выполнения позволяют студенту самостоятельно изучить соответствующий раздел курса.
Пособие рекомендуется студентам специальности 2204 “Программное обеспечение вычислительной техники и автоматизированных систем” при изучении курса «Информатика», студентам специальности 0611 «Менеджмент» и направления 5515 при изучении курса «Электронно-вычислительные машины и вычислительные сети»
Подготовлено к публикации кафедрами «Программного обеспечения вычислительных систем» и «Вычислительных машин и комплексов.»
1. Позиционные системы счисления
Выполнение любых вычислений базируется на определенной форме представления чисел. Это определяется принятой системой счисления - совокупностью символов и правил для представления чисел. Символы называются цифрами данной системы счисления. Системы счисления могут быть позиционными и непозиционными.
Непозиционной системой называется такая, в которой значение символа не зависит от его места расположения в числе. Для образования числа в непозиционной системе счисления используются операции арифметического сложения и вычитания. Примером непозиционной системы счисления является римская:
XVI=X+V+I=10+5+1=1610
IX=X-I=10-1=910
В позиционной системе счисления значение каждого символа-цифры зависит от его места расположения в числе. Справедливо следующее представление числа в позиционной системе счисления:
x(q) = a n-1 q n-1 + a n-2 q n-2+ ... +a 1q1 + a0q0 + a-1q-1 + ...+amqm
где:
x(q) - число в системе счисления с основанием q;
a i - цифра i-ого разряда в числе;
n - количество целых разрядов числа;
m - количество дробных разрядов числа.
Под основанием системы счисления q, с одной стороны, понимают количество различных цифр, ее образующее, а с другой стороны - число, показывающее во сколько раз вес цифры данного разряда меньше веса соседнего старшего разряда.
Очевидно, что используемая система счисления определяет набор правил (алгоритмов) выполнения операций над числами. Поэтому важное значение имеет правильное представление чисел и преобразование чисел в различных системах счисления.
Наибольшее распространение в вычислительной технике имеют системы счисления с основаниями 2,8,16 - двоичная, восьмеричная, шестнадцатеричная.
1.1. Перевод чисел из одной системы счисления в другую.
Здесь различают три ситуации при переводе чисел:
- перевод числа из десятичной системы в систему с любым основанием;
- перевод числа из системы с любым основанием в десятичную;
- перевод числа из системы с основанием q1 в систему с основанием q2.
?
?
Правила, используемые для перевода целых и дробных чисел различны.
Для перевода целого числа из десятичной системы счисления в систему с основанием q, число нужно последовательно делить на основание q до тех пор, пока не будет получена целая часть частного, равная 0, то есть будет получен остаток от деления, меньший q. Число в системе счисления с основанием q записывается в виде упорядоченной последовательности остатков от деления в порядке, обратном получению остатков, то есть старшей цифрой числа будет последний остаток.
При переводе числа в шестнадцатеричную систему счисления необходимо помнить, что шестнадцатеричные числа представляются символами 1, 2, ..., 8, 9, A(10), B(11), C(12), D(13), E(14), F(15).
Для перевода правильной дроби из десятичной системы счисления в систему с основанием q число нужно последовательно умножать на основание q (причем умножению подвергаются только дробные части) до тех пор, пока не будет обеспечена заданная точность представления числа. Дробь в системе счисления с основанием q записывается в виде упорядоченной последовательности целых частей произведений в порядке их получения. Если требуемая точность перевода q, то число указанных последовательных произведений (то есть цифр в представлении дроби) равно k+1. По (k+1)-ой цифре производится округление k-той цифры.
Пример : перевести число 9510 в следующие системы счисления:
а) двоичную:
| 95 | 2 | ||||||
| 94 | 47 | 2 | |||||
 1 1
| 46 | 23 | 2 | ||||
| 1 | 22 | 11 | 2 | ||||
| 1 | 10 | 5 | 2 | ||||
| 1 | 4 | 2 | 2 | ||||
| 1 | 2 | 1 | 2 | ||||
| направление записи числа | 0 | 0 | 0 | ||||
| 1 | |||||||
| Ответ:9510 = 10111112 | |||||||
б) восьмеричную :
| 95 | 8 | ||
| 88 | 11 | 8 | |
| 7 | 8 | 1 | 8 |
| 3 | 0 | 0 | |
| 1 | |||
| Ответ:9510 = 1378 | |||
|
| |||
в) шестнадцатеричную:
| 95 | 16 | ||
| 80 | 5 | 16 | |
| F | 0 | 0 | |
| 5 | |||
| Ответ:9510 = 5F16 | |||
Если на некотором шаге получения произведений дробная часть числа становится равной 0, то процесс преобразования на этом заканчивается, так как все остальные цифры в представление дроби будут равны 0.
Пример: перевести число 0.95 в следующие системы счисления, с точностью представления 2, 8, 16, соответственно:
а) двоичную СС: б) восьмеричную СС: в) шестнадцатеричную СС:
| 0 | 95 |
| 0 | 95 | 0 | 95 | ||
| 2 |
| 8 | 16 | |||||
| 1 | 90 |
| 7 | 60 | F | 20 | ||
| 2 |
| 8 | 16 | |||||
| 1 | 80 |
| 4 | 80 | 3 | 20 | ||
| 2 |
| 8 | 16 | |||||
| 1 | 60 |
| 6 | 40 | 3 | 20 | ||
| 2 |
| |||||||
| 1 | 20 | |||||||
| 2 | ||||||||
| 0 | 40 | |||||||
| 2 | ||||||||
| 0 | 80 | |||||||
| 2 | ||||||||
| 1 | 60 | |||||||
Ответ: 0.9510 = 0.1111012 = 0.758 = 0.F316
При переводе неправильной дроби из десятичной системы счисления в систему с основанием q отдельно переводится целая и дробная части числа.
Пример: перевести число 123.58 в восьмеричную систему счисления.
123.5810 =12310 + 0.5810 = 1738 + 0.458 = 173.458
Для перевода числа из системы счисления с основанием q в десятичную пользуются формулой разложения в ряд (1). Выражение (1) справедливо как для целых, так и для дробных чисел.
Пример: представить числа: а)111011.011, б)154.31, в)А2В.3С в десятичной системе счисления.
111011.0112 = 1*25 +1*24 +1*23 +0*22 +1*21 +1*20 +0*2-1 +1*2-2 +1*2-3 =
=32 +16+8+2+1+1/4+1/8=59.37510
154.318 = 1*82 +5*81 +4*80 +3*8-1 +1*8-2 = 64+ 40+ 4+ 3/8+ 1/64 =
=108.39062510
А2В.3С16 = А*162 +2*161 +В*160 +3*16-1 +С*16-2 = 3840+32+11+3/16+12/256 = 3883.23437510
При переводе чисел из системы счисления с основанием q1 в систему с основанием q2 выполняется промежуточное преобразование в десятичную систему.
1.2. Связь двоичной, восьмеричной и шестнадцатеричной систем счисления.
Восьмеричная и шестнадцатеричная системы счисления относятся к двоично-кодированным системам, основание которых представляют целые степени двойки: 23 - для восьмеричной и 24 - для шестнадцатеричной.
Каждая восьмеричная цифра представляется триадой двоичных цифр, а каждая шестнадцатеричная цифра - тетрадой двоичных цифр.
Перевод целых и дробных чисел из двоичной в восьмеричную и из двоичной в шестнадцатеричную системы счисления производится с учетом следующих таблиц:
Таблица 1
| Восьмеричное число | Триада |
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Таблица 2
| Шестнадцатеричное число | Тетрада |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
Для перевода двоичного числа в восьмеричную (шестнадцатеричную) систему счисления число разбивается на триады (тетрады) двоичных цифр. Причем для целого числа триады (тетрады) находятся, начиная с младшего разряда, двигаясь влево к старшему разряду. Если старшая триада (тетрада) не получается из-за нехватки цифр, то слева к числу приписывается нужное количество нулей. Для дробного числа триады (тетрады) находятся, начиная со старшего разряда, двигаясь вправо к младшему. Если количество разрядов не кратно трём (четырем), то справа приписывается нужное количество нулей. Далее каждой триаде (тетраде) ставится в соответствие восьмеричная (шестнадцатеричная) цифра.
При обратном переводе вместо каждой восьмеричной (шестнадцатеричной) цифры записывается эквивалентная ей триада (тетрада) двоичных. Положение запятой между целой и дробной частями числа сохраняется. Нули слева от целой части и справа от дробной части опускаются.
Примеры:
| а) | 1101110011.01101012 | = | 001 | 101 | 110 | 011. | 010 | 100 | = | 1563 . 3248 | ||||||||
| 1 | 5 | 6 | 3 | 2 | 4 | |||||||||||||
| б) | 2076.3058 = | 2 | 0 | 7 | 6 , | 3 | 0 | 5 | = | 10000111110,0110001012 | ||||||||
| 10 | 000 | 111 | 110, | 011 | 000 | 101 |
| |||||||||||
| в) | 11011011110100.10110011012= | 0011 | 0110 | 1111 | 0100, | 1011 | 0011 | 0100 | = |
| 3 | 6 | F | 4 | B | 3 | 4 |
= 36F4.B3416
г) A2E.С1D16 = 101000101110.1100000111012
2. Формы представления чисел в ЦВМ
В памяти ЦВМ числовая информация может быть представлена в различных формах.
В случае с фиксированной запятой для всех чисел, над которыми выполняются операции, положение запятой строго зафиксировано между целой и дробной частями числа.
Обычно в ЦВМ используются два способа расположения запятой:
перед старшим разрядом, то есть целая часть числа равна нулю, и в операциях участвуют правильные дроби;
после младшего разряда, то есть дробная часть числа равна нулю, и в операциях участвуют только целые числа.
Разрядная сетка с указанием номера разряда и его веса для дробного числа имеет вид:
| 2-1 | 2-2 | 2-3 | 2-(n-1) | 2 -n | ||
| 0 | 1 | 2 | 3 | ... | n-1 | n |
| Знак | цифровая часть числа | |||||
Разрядная сетка для целого числа имеет вид:
| 2n-1 | 2n-2 | 21 | 20 | |||
| n | n-1 | … | … | … | 1 | 0 |
| знак | цифровая часть числа | |||||
Если целые числа представляются без знака, то диапазон их представления в заданной разрядной сетке может быть увеличен за счет использования разряда, отводимого под знак числа.
Число с фиксированной запятой представляется следующим образом:
[Х]ф.з.=Х*Км , (2)
где : [Х]ф.з.- машинное представление числа с фиксированной запятой;
Х - исходное число,
Км - масштабный коэффициент, который выбирается из условий конкретной разрядной сетки и не должен допускать выхода исходных чисел и результатов вычислений за пределы допустимого диапазона.
Масштабный коэффициент должен быть единым для всех обрабатываемых в машине чисел и получаемых результатов, он хранится отдельно от представляемых чисел и учитывается при выдаче конечного результата.
Число в форме с фиксированной запятой должно удовлетворять следующему неравенству:
[X]ф.з.min £ [X]ф.з. £ [X]ф.з.max (3)
Если нарушена левая часть неравенства, то имеем машинный ноль; если нарушена правая часть неравенства, то произошло переполнение разрядной сетки.
Представление чисел в форме с плавающей запятой позволяет избежать масштабирования исходных чисел, а также увеличить диапазон и точность представляемых чисел.
Число в нормальной форме имеет вид:
Х = m*q p , (4)
Где: q- основание СС,
p -целое число - порядок числа Х,
m -мантисса числа.
Полулогарифмической эта форма представления называется потому, что в логарифмической форме представлено не всё число, а только его характеристика q.
Поскольку, изменяя одновременно определённым образом мантиссу и порядок числа Х, можно по выражению (4) получить любое количество представлений числа Х, то на мантиссу m накладывается следующее ограничение, чтобы избежать неоднозначности в представлении чисел
q -1 £ I mI £ 1. (5)
Если для числа Х в форме с плавающей запятой выполнены условия (5), то число Х называется нормализованным, мантисса представляется правильной дробью, а ее старший разряд с основанием q отличен от 0.
Для двоичной СС неравенство (5) имеет вид:
0.100...0 £ lml £ 0.11...1 . (5')
Разрядная сетка для числа с плавающей запятой состоит из двух частей: для порядка и для мантиссы.
| порядок | мантисса | ||||||
| m-1 | m-2 | 0 | 0 | 1 | 2 | n | |
| Знак порядка | 2 m-1 | 2 m-2 | 2 -0 | Знак мантиссы | 2-1 | 2-2 | 2 -n |
Мантисса, удовлетворяющая условию (5') называется нормализованной, а операция преобразования ее к виду (5') называется нормализацией.
Чтобы нормализовать мантиссу, ее нужно сдвигать вправо для целого числа и влево для дроби на столько разрядов, чтобы целая часть мантиссы была равна нулю, а старший разряд мантиссы был равен 1, после чего к порядку целого числа прибавить (а из порядка дроби вычесть) столько единиц, на сколько разрядов был произведен сдвиг.
Для упрощения операций над порядками чисел с плавающей запятой, порядки представляют целыми положительными числами без знака, используются так называемые смещенные порядки. Чтобы получить смещенный порядок, нужно к исходному порядку p прибавить целое число - смещение М = 2 k , где k-число двоичных разрядов, используемых для модуля порядка.
Смещенный порядок
Рсм = Р+М (6)
всегда является положительным. Для его представления необходимо такое же число разрядов, как и для модуля и знака порядка р.
3. Кодирование отрицательных чисел.
Отрицательные числа в ЭВМ представляются в прямом, дополнительном и обратном кодах.
При представлении числа в прямом коде код числа в разрядной сетке из n разрядов совпадает с самим числом.
В двоичной системе счисления знаки кодируются следующим образом: «+» цифрой 0, «-« цифрой 1. Знаковый разряд располагается слева от значащих цифр числа, то есть это крайний левый разряд в представление числа. При таком подходе введение знакового разряда уменьшает диапазон представления положительных и отрицательных чисел. Вес знакового разряда соответствует весу старшего разряда разрядной сетки. Значащие разряды числа занимают n -1 разряд. Диапазон представления положительных чисел 0 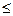 X
X 
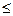 2n-1 –1, а отрицательных 0
2n-1 –1, а отрицательных 0 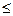 X
X 
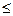 -(2n-1 – 1).
-(2n-1 – 1).
X, при X ³ 0
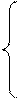 [X] пр = (7)
[X] пр = (7)
q n-1 +lXl, при X £ 0
где q n-1 величина, равная весу старшего разряда (для дробных чисел q n-1 =1).
Обратите внимание на то, что запись числа в форме (7) приводит к двум равнозначным формам записи нуля – «положительной» и «отрицательной».
Примеры: представить в прямом коде следующие числа:
1. а) Х1 = +110112; б) Х3 = +0.110112
Х2 = -110112; Х4 = -0.110112
2. а) Х1 = +7318; б) Х3 = +0.7318
Х2 = -7318; Х4 = -0.7318
3. а) Х1 = +В13; б) Х3 = +0.В13
Х2 = -В13 ; Х4 = -0.В13
Ответы:
1. qn-1 = 25 = 100000
а) [X1] пр = 011011 , [X2] пр = 111011
Здесь и далее знаковый разряд будет отмечаться подчёркиванием.
б) [X3] пр = 0.11011
[X4] пр = 1.11011
Точка в результате используется нами только для указания того, что число представлено правильной дробью и, следовательно, всегда меньше 1. Этот знак не является частью числа и в машинном представлении опускается.
2. qn-1 = 83 = 1000
а) [X1] пр = 0.731 б) [X3] пр = 0.731
[X2] пр = 1.731 [X4] пр = 1.731
3. q n-1 = 163 = 1000
а) [X1] пр = 0.B13 б) [X3] пр = 0.B13
[X2] пр = 1.B13 [X4] пр = 1.В13
Дополнительный код отрицательного числа представляет собой дополнение модуля исходного числа Х до q n, где n - количество разрядов целой части числа Х. Для правильной дроби q n= 10 в соответствующей системе счисления.
Поэтому для целого числа:
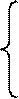 |
Х, при Х>=0
[X] доп = (8)
q n -  X
X  , при X<0
, при X<0
Для правильной дроби:
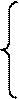 |
Х, при Х>=0
[X] доп = (9)
1- 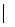 X
X 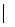 , при X<0
, при X<0
Дополнительный код очень удобен при сложении чисел со знаком и вычитании. Действительно, если для трёхразрядного положительного числа B в любой системе счисления дополнение равно Bдоп= 1000 - 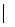 B
B  , то разность
, то разность
A – B = A + {1000 -  B
B  } – 1000 = A+Bдоп –1000.
} – 1000 = A+Bдоп –1000.
Таким образом, вычитание сводится к сложению с дополнением вычитаемого. Единица , возникающаая за пределами разрядной сетки за счёт вычитания 1000 должна быть отброшена.
Старший разряд двоичного числа в дополнительном коде имеет смысл знакового разряда. Его нулевое значение соответствует положительному числу, а единичное – отрицательному.
Перевод в дополнительный код для двоичной системы счисления может быть выполнен по следующему правилу: все разряды двоичного числа, включая знаковый, инвертируются и к результату прибавляется единица младшего разряда.
Примеры: перевести в дополнительный код следующие числа:
1. а) Х1 = +11011; Х2 = -(X1); б) Х3 = +0.11011; Х4 = -(X3);
2. а) Х1 = +731; Х2 = -(X1); б) Х3 = +0.731; Х4 = -(X3);
3. а) Х1 = +В13; Х2 = -(X1); б) Х3 = +0.В13; Х4 = -(X3);
Ответы:
1. q n = 26 = 1000000
а) [X1]доп= 011011; [X2] доп =1000000 – 011011= 100101;
или [X2] доп = 100100 + 000001 = 100101;
б) [X3] доп = 0.11011 [X4] доп = 10.00000 – 0.11011 =1.00101;
или [X4] доп = 1.00100 + 0.000001 = 1.00101
2. q n = 84 = 10000
а) [X1] доп = 0731; [X2] доп =10000 – 0731= 7047;
б) [X3] доп = 0.731 [X2] доп =1.0000 – 0.731= 7.047;
3. q n+1 = 164 =1 0000
а) [X1] доп = 0.0В13
[X2] доп = 1.F4ЕС + 0.0001 = 1.F4ED
б) [X3] доп = 0.B13
[X4] доп = 1.4ЕС + 0.001 = 1.4ED
Обратный код отрицательных чисел представляется как дополнение модуля исходного целого числа Х до q n+1 и модуля исходной правильной дроби до 1 0 в соответствующей СС без единицы младшего разряда числа.
Если к представлению исходного числа в обратном коде прибавить единицу младшего разряда, то получим исходное число в дополнительном коде.
4. Сложение чисел в форме с фиксированной запятой.
Сложение чисел в прямом коде очень просто выполняется для чисел с одинаковыми знаками. Числа складываются, а их сумме присваивается код знака слагаемых.
Если числа имеют разные знаки, то используется операция алгебраического сложения (вычитания). Из большего по модулю числа вычитается меньшее по модулю число, их разности присваивается код знака большего по модулю числа.
Гораздо проще в этом случае использовать дополнительный код для отрицательных чисел. Тогда операция алгебраического сложения сводится к простому арифметическому сложению. Знаковый разряд и цифровая часть числа рассматриваются как единое целое. Машина оперирует с отрицательными числами, представленными в дополнительном коде, как с положительными независимо от того, целые они или дробные. Сумма также получается в дополнительном коде. Правильный знак суммы получается автоматически в процессе суммирования знаковых цифр операндов и цифры переноса из соседнего младшего разряда.
В случае возникновения единицы переноса из знакового разряда суммы ее нужно отбросить ("погасить") при сложении в дополнительном коде; прибавить к младшему разряду суммы при сложении в обратном коде (циклический перенос единицы переполнения ).
Суммирование двоичных чисел происходит в соответствии с таблицей сложения, причем в каждом i-том разряде участвуют в сложении три цифры: цифра переноса из соседнего младшего разряда Pi и две цифры соответствующего разряда Ai и Bi. В результате сложения имеем сумму Si в данном i-том разряде и перенос в следующий (i+1)-ый разряд Pi+1.
Таблица 3.
| Pi | Ai | Bi | Si | Pi+1 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Пример: произвести сложение в дополнительном коде следующих пар чисел; результат представить в прямом и дополнительном кодах:
1. а) X1 = 010101 б) X1 = -(010101)
X2 = -(001001) X2 = 0010001
|
а) [X1]доп. = 010101
[X2] доп. = 110111

 [X cум]доп. = 1001100
[X cум]доп. = 1001100
|
гасится
б) [X1]доп. = 101011
[X2] доп. = 001001
 [X cум]доп. = 110100
[X cум]доп. = 110100
[X cум]пр = 101011 + 000001 = 101100
Ответ: [X cум]доп. = 110100 [X cум]пр = 101100
2. а) X1 = +3В16 б) X1 = -3В
X2 = -С216 X2 = +С2
а) [X1]доп= 03В (для разрядной сетки цифровой части числа n=3 )
[X2]доп= F3E
 [X cум]доп = F79
[X cум]доп = F79
Результат отрицательный, для записи его в прямом коде найдём дополнение
[[X cум]доп]доп = 1000 – F79 = 87, что даёт значение результата с обратным знаком ( дополнение дополнения). При записи суммы в прямом коде необходимо восстановить знак.
В сложении участвуют целые числа, поэтому в разрядной сетке результат сложения расположен следующим образом:
зн 162 161 160
| 1 | 0 | 8 | 7 |
Ответ: [X cум]доп = F79 ; [X cум]пр = -108716; X cум = - 87
б) [Х1] доп = 1FC5
[X2] доп = 00С2
 |
 [X cум]доп = 10087
[X cум]доп = 10087
гасится
Так как знак суммы положительный, то её дополнительный код совпадает с прямым.
Ответ: Х = 8716
5. Формирование признака переполнения разрядной сетки
При алгебраическом сложении двух чисел, помещающихся в разрядную сетку, может возникнуть переполнение, то есть образоваться сумма, для представления которой разрядная сетка должна содержать на один разряд больше, чем разрядная сетка для представления слагаемых.
Признак обнаружения переполнения разрядной сетки формируется следующим образом: если при сложении двух чисел в дополнительном (обратном) коде существует перенос в знаковый разряд суммы при отсутствии переноса из её знакового разряда, или же существует перенос из знакового разряда суммы при отсутствии переноса в её знаковый разряд, то фиксируется ситуация переполнения разрядной сетки, причем в первом случае - положительное переполнение, а во втором - отрицательное.
Если и в знаковый и из знакового разряда суммы перенос существует или его нет, то переполнение отсутствует.
При положительном переполнение результат операции положительный, а при отрицательном - отрицательный.
Пример: сложить следующие пары чисел в дополнительном коде:
а) Х1 = +01010 б) Х1 = -01101
Х2 = +01011 Х2 = -01001
а) [X1] доп = 01010
[X2] доп = 01011
 |
[X cум]доп = 10101
Результат сложения двух положительных чисел получился с отрицательным знаком, что невозможно. Но при сложение существовал перенос в знаковый разряд суммы при отсутствии его из знакового разряда. Это ситуация положительного переполнения разрядной сетки. Единица, находящаяся в знаковом разряде - это старший разряд суммы, знак которой должен быть положительным.
Ответ: [X cум] доп =[Xcум] пр = 010101 или X cум =+10101
б) [X1] доп = 10011
[X2] доп = 10111
 |
[X cум]доп = 101010
По правилу сложения в дополнительном коде единица переполнения из знакового разряда должна быть погашена, но результат сложения двух отрицательных чисел получится положительным, что невозможно. В этом случае существовал перенос из знакового разряда при отсутствии переноса в знаковый. Имеет место отрицательное переполнение разрядной сетки. Единица переполнения из знакового разряда - это отрицательный знак результата, а ноль в знаковом разряде - старший разряд суммы в дополнительном коде.
Поэтому: [X] доп = 101010; [X2] пр= 110110
Примечание: рассмотренные в 2.6 и 2.7 примеры показывают только механизм выполнения операций и не учитывают особенности размещения чисел в памяти ЭВМ. При выполнении сложения и вычитания чисел с разрядностью n разрядность результата может быть 2 n. Размер разрядной сетки ЭВМ всегда фиксирован и в случае её переполнения запоминание единицы переполнения осуществляется в отдельном регистре.
6. Умножение целых двоичных чисел
Операция умножения двоичных чисел реализуется в ЭВМ с применением операций сложения и сдвига. Возможные варианты выполнения операции представлены в табл. 4.
Таблица 4.
| Разряды множителя, с которого начинается умножение | Вариант умножения | Направление сдвига в процессе умножения | ||
| множимое | множитель | сумма частичных произведений | ||
| младшие | 1 | неподвижно | вправо | вправо |
| 2 | влево | вправо | неподвижно | |
| старшие | 3 | неподвижно | влево | влево |
| 4 | вправо | влево | неподвижно | |
В основном в ЭВМ применяется 1-ый вариант умножения младшими разрядами вперёд с неподвижным множимом при сдвиге суммы частичных произведений вправо на один разряд за такт. Умножение производится по следующему правилу: проверяется младший разряд множителя; если там единица, то к ранее полученной сумме частичных произведений прибавляется неподвижное множимое, после чего осуществляется сдвиг суммы вправо на один разряд; если в младшем разряде множителя ноль, то сдвиг осуществляется без суммирования. Описанная операция повторяется столько раз, сколько цифр содержит множитель, причем после каждого такта выполнения этих операций множитель сдвигается вправо на один разряд, чтобы следующая его цифра на каждом такте выполнения операции умножения занимала место младшего разряда множителя. При умножении целых двоичных цифр без знака, то есть их модулей, множимое и множитель представляются каждый в виде n-разрядного слова, а их произведения в виде 2n-разрядного слова.
7. Лабораторная работа «Представление цифровых данных в ЦВМ»
7.1. Цель работы.
Изучить формы представления чисел в различных системах счисления и правила выполнения арифметических операций над ними.
7.2. Порядок выполнения работы.
7.2.1. Сформировать три исходных числа А1, А2, А3 в десятичной системе счисления, согласно табл. 5.
Таблица 5
Варианты исходных чисел
| Номер варианта | А1 | А2 | А3 | ||||
| цифры | цифры | цифры | |||||
| 1 | 2 | 3 | 1 | 2 | 1 | 2 | |
| 1-9 | NB | NV | NGR | NV | NGR | 10-NV | NB+NGR |
| 10-18 | NV* | NV+NB | NGR | NV-9 | NGR+3* | NV-9 | NGR+7* |
| 19-27 | NV+NB* | NB | NGR | NV-18* | NGR+6* | NV-18 | NGR |
Число А1 - трехразрядное, числа А2 и А3 двухразрядные.
В табл.5 приведены следующие обозначения:
· NB - произвольное число, например, месяц рождения;
· NV - номер варианта;
· NGR - последняя цифра номера группы для групп, имеющих четырех и пятизначные номера.
Для групп с трехзначными номерами NGR задается преподавателем.
Примечание: при формировании чисел А1,А2,А3, если в формулах получается двухразрядное число, то нужно просуммировать цифры обоих разрядов для получения одноразрядного числа.
7.2.2. Осуществить перевод числа W=А2,А3 ( А2 - целая часть числа W, А3 - дробная), заданного в десятичной СС в системы счисления с основаниями 2,8,16. При переводе дробной части числа задается следующая точность представления:
· для двоичной СС - 6 разрядов после запятой
· для восьмеричной и шестнадцатеричной 2 разряда после запятой.
7.2.3. Выполнить перевод числа А1 в системы счисления с основаниями 8 и 16.
Полученное после перевода число представить в следующем формате (формат с фиксированной запятой):
номера разрядов
| n-1 | n-2 2 1 0 |
| знаковый разряд | разряды цифровой части |
7.2.4. Перевести число +(-)А1 (положительное и отрицательное) в дополнительный код.
7.2.5. Выполнить над числами А2 и А3 следующие операции:
(А2+А3), (А2-А3), (-А2+А3), (-А2-А3).
Операции выполнять в дополнительном коде в двоичной системе счисления
Числа А2 и А3 представляются в формате с фиксированной запятой. Результат записать в прямом и дополнительном кодах. Результаты перевести в восьмеричную и шестнадцатеричную системы.
Выявить возможные случаи переполнения.
7.2.6. Выполнить над числами А2 и А3 следующие операции:
(А1+А2), (А1-А2), (-А1+А2), (-А1-А2).
Операции выполнять в дополнительном коде в шестнадцатеричной системе счисления.
Числа А1 и А2 - целые беззнаковые числа, представленные в следующем формате:
номера разрядов
| n-1 n-2 … 1 0 |
| разряды цифровой части |
Результаты представить в шестнадцатеричной и двоичной системах.
7.2.7. Выполнить операцию умножения чисел А2 и А3 в двоичной СС (А2 и А3 - целые числа без знака).
7.2.8. Представить число W, определенное в п.3.2 задания в форме с плавающей запятой в двоичной восьмеричной и шестнадцатеричной системах счисления. Какое количество разрядов в указанных системах счисления необходимо отвести под порядок числа?
7.2.9. Результаты выполнения заданий по п.п. 3.1-3.8 привести в отчете по лабораторной работе.
7.3. СОДЕРЖАНИЕ ОТЧЁТА
§ Титульный лист.
§ Цель работы.
§ Результаты выполнения индивидуального задания. В отчете должен быть представлен весь порядок выполненных вычислений.
§ Выводы по работе.
Литература
1. Савельев А.Я. Основы информатики: Учеб. Для вузов.- М.: Изд-во МГТУ им. Н.Э.Баумана, 2001.- 328 с.
2. Лысиков Б.Г. Арифметические и логические основы цифровых автоматов. - Мн.: Высшая школа, 1980. -336 с.
3. Савельев А.Я. Прикладная теория цифровых автоматов: Учеб.для вузов по спец.ЭВМ.- М: Высш. Шк., 1987.-272 с.
4. Приложение
КОНТРОЛЬНЫЙ ПРИМЕР
выполнения лабораторной лаботы
Предположим, что N группы (NGR) 4103; номер варианта (NV)13, номер бригады (NB) 9. Поэтому по табл.5 формируем числа : А1 = 45310; А2 = 4610; А3 = 4110
W = A2, A3 = 46,4110
1. Осуществляется перевод числа W = 46,41 в а) двоичную, б) восьмеричную и в) шестнадцатеричную СС. Причем обеспечить точность перевода для g=2 6 разрядов после запятой; для g=8, g=16 - два после запятой.
 а) 46 2
а) 46 2
 |  | ||||
 | |||||
46 23 2 0 , 41



 2
2
0 22 11 2 0 , 82



 2
2
1 10 5 2 0 , 64

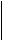

 2
2
1 4 2 2 1 , 28

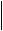
 2
2
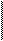 1 2 1 2 0 , 56
1 2 1 2 0 , 56


 2
2
0 0 0 1 , 12
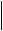
 2
2
1 0 , 24
2
0 , 48
При переводе дроби получаем 7 разрядов после запятой, и по значению 7-ого разряда округляем 6-ой.
Ответ: W=46,4110 ~101110,0110102
 б)
б)

 46 8
46 8
 0 , 41
0 , 41
 40 5 8 8
40 5 8 8

 3 , 28
3 , 28
6 0 0 8
 2 , 24 W=46,4110 ~56,328
2 , 24 W=46,4110 ~56,328
5 8
1 , 92
Если же воспользоваться связью двоичной и восьмеричной СС и осуществить перевод по триадам, то имеем
W = 46,4110 = 101110, 0110102 = 56,328
Ответ: W = 46,4110 = 56,328
| б) | 46 | 16 | 0 | 41 | ||||
| 32 | 2 | 16 | 16 | W = 46,4110 = 2E,6816 | ||||
| E | 0 | 0 | 6 | 56 | ||||
| 2 | 16 | |||||||
| 8 | 96 | |||||||
Если воспользоваться связью двоичной и шестнадцатеричной СС и осуществить перевод по тетрадам, то имеем
W = 46,4110 = 101110,0110102 =2 E,6816
Ответ: W = 46,4110 = 2E,6816
2. Перевести число А1 в а) восьмеричную и шестнадцатеричную СС; б) полученные числа представить в формате для целых чисел с фиксированной запятой; в) перевести число +А18,16, -А18,16 в дополнительный код.
а) А1 = 45310 = 7058 = 1С516
б) Пусть имеем разрядную сетку следующего вида :
| 4 | 3 | 2 | 1 | 0 |
| знак | 83 | 82 | 81 | 80 |
| 163 | 162 | 161 | 160 |
старший разряд отводится под знак и с 0 по 3-ый разряды цифровой части числа.
Ответ:
| 0 | 0 | 7 | 0 | 5 | ; | 0 | 0 | 1 | С | 5 |
в) +А1 = +7058
-А1 = -7058
Если для цифровой части числа отвести 4 разряда ,то имеем
[+А1]доп = 0,0705
[-А1]доп = 1,7072+0,0001 = 1,7073
+А1 = +1С516
-А1 = -1С516
Если для цифровой части числа отвести 4 разряда ,то имеем
[+А1]доп = 0,01С5
[-А1]доп = 1,FE3B+0,0001 = 1,FE3C
3. Выполнить над числами А2 и А3 следующие операции :
а) (А2+А3); б) (А2-А3); в) (-А2+А3); г) (-А2-А3).
Число представленное в форме с фиксированной запятой, является правильными дробями (т.е. 0,А2 и 0,А3) и записывается в форме
| 0 знак | 1 | 2 | 3 | 4 | 5 | 6 |
| 2-1 | 2-2 | 2-3 | 2-4 | 2-5 | 2-6 |
0,А2 = 0,4610 = 0,0111012 0,А3 = 0,4110 = 0,0110102
а)
[+0,А2]доп = 0,011101
+ Ответ:[А сумм]пр =[А сумм] доп =0,110111
[+0,А3] доп = 0,011010

[А сумм] доп = 0,110111
б) [+0,А2]доп = 0,011101
+ Ответ:[А сумм]пр =[А сумм] доп =0,000011
[-0,А3]доп = 1,100110
 |

 [А сумм]доп = 10,000011 гасится
[А сумм]доп = 10,000011 гасится
в) [-0,А2]доп = 1,100011
+ Ответ: [А сумм] доп= 1,111101
[+0,А3]доп = 0,011010 [А сумм]пр= 1,000011
 |
[А сумм]доп = 1,111101
г) [-0,А2]доп = 1,100011
+ Ответ: [А сумм]доп = 1.001001
[-0,А3]доп = 1,100110 [А сумма]пр = 1.110111

[А сумм] = 11,001001
 гасится
гасится
Ситуации переполнения разрядной сетки не были.
4. Выполнить над числами А1 и А2, которые являются целыми, беззнаковыми, представленными в шестнадцатеричной СС следующие операции в дополнительном коде:
а) (А1+А2); б) (А1-А2); в) (-А1+А2); г) (-А1-А2)
А1 = 45310 = 1С516; А2 = 4610 = 2Е16
Если под цифровую часть чисел отводится 3 разряда, то имеем:
а) [+А1]доп = 01С5
+ Ответ: :[А сумм]пр =[А сумм] доп =01F316
[+А2]доп = 002Е А сумм = 1F316
 [Асумм]доп= 01F3
[Асумм]доп= 01F3
б) [+А1]доп = 01С5
+ Ответ: :[А сумм]пр =[А сумм] доп.=019716
[-А2]доп = 1F2 Асумм=19716
 |
 [Асумма]доп = 10197
[Асумма]доп = 10197
гасится
в) [-А1]доп = 1Е3В
+ Ответ: [А сумм] доп= 1Е69; : [Асумм]пр = 119716
[+А2]доп = 002Е Асумм = -19716

[Асумм]доп = 1Е69
г) [-А1]доп = 1.Е3В
+ Ответ: [А сумм] доп= 1Е1D16; [Асумм]пр = 11 F 316
[-А2]доп = 1.FD2 Асумм = -1F316
 |
 [Асумм]доп = 11.Е1D
[Асумм]доп = 11.Е1D
гасится
5. Найти произведение чисел А2 и А3 в двоичной СС, если А2 и А3 - целые числа без знака.
А2=4610 = 1011102 А3=4110 =1010012
0 0 0 0 0 0
+ 1 0 1 1 1 0

1 сумма 1 0 1 1 1 0
1 сдвиг 0 1 0 1 1 1 0
2 сдвиг 0 0 1 0 1 1 1 0
3 сдвиг 0 0 0 1 0 1 1 1 0
4 сумма + 1 0 1 1 1 0

1 1 0 0 1 1
4 сдвиг 0 1 1 0 0 1 1 1 1 0
5 сдвиг 0 0 1 1 0 0 1 1 1 1 0
5 сумма + 1 0 1 1 1 0

1 1 1 0 1 0
6 сдвиг 0 1 1 1 0 1 0 1 1 1 1 0
Ответ: А2хА3 = 111010111102 = 188610
6. Представить число W = 46.4110 в форме с плавающей запятой в:
а) двоичной СС
б) восьмеричной СС
в) шестнадцатеричной СС,
Определить количество разрядов для представления порядка в этих СС.
а) W=46.4110 = 101110,0110102
W=0.101110011010*26 = 0.101110011010 * 100.110
W=m*10 p . Для представления р = +110 нужны 1 разряд под знак и три разряда под цифровую часть числа.
б) W=46.4110 = 56.328
W=0.5632, (8)*82 = 0.5632*100.2
Для представления р = +28 нужен один разряд под знак и 1 разряд под цифровую часть числа
в) W=46.412 = 2E.6816
W=0.2E6816 * 162 = 0.2E6816 * 100.216
Для представления р = +216 нужны один разряд под знак и 1 разряд под цифровую часть числа.








