2 . 5. Імовірнісні та сигнатурні методи контролю

Дата: 2025-05-21; Просмотры: 5

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Вади алгоритмічних методів, про які йшла мова, стимулювали пошук інших підходів до тестового контролю цифрових пристроїв. Ці пошуки продовжуються і сьогодні, але вже є й вагомі здобутки, результати яких широко застосовують на практиці.

З появою ВІС із функціями рівня мікропроцесора стало очевидним, що алгоритмічний підхід не може забезпечити необхідну ефективність діагностування пристроїв такої і більш високої складності. Це проявилося в тому, що значна частина несправностей при тестуванні в виробничих умовах не виявлялася, що призводило до не виявлення дефектних виробів.

Основна ідея нових методів полягає у пошуку деяких інтегральних ознак працездатності, які не обов’язково пов’язані із виконанням об’єктом своїх функцій. Наприклад, значення струму живлення у багатьох випадках є досить надійною ознакою працездатності чи непрацездатності об’єкту. Зрозуміло, що така ознака є досить грубим критерієм працездатності і тому не може забезпечити необхідну достовірність контролю. Але в той же час цей приклад досить виразно характеризує напрямок пошуку. Іншим прикладом такого інтегрального підходу є імовірнісний метод [ ], суть якого полягає у наступному.

На входи об’єкта подаються випадкові двійкові послідовності, які мають фіксовану ймовірність появи 0 і 1 – 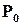і 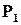(це еквівалентно відносній частоті появи 0 і 1). Можна показати, що будь-який цифровий пристрій є одночасно перетворювачем ймовірностей 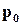і 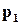. Враховуючи, що 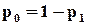, можна записати 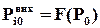, , 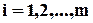де 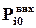– ймовірність появи 0 на і-му виході пристрою, 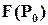- деяка цілком визначена арифметична функція, яка однозначно залежить від логічних функцій, які виконує пристрій, 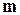- кількість виходів пристрою. Оскільки будь-яка несправність змінює логічні функції пристрою (якби це було не так, то несправність не можна було б виявити), то фіксуючи 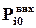, можна визначити наявність (відсутність) несправності. Для пояснення наведемо прості приклади.

Якщо на входи схеми “І” подавати сигнали з 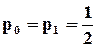, то на виход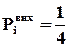і

і ,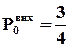

що можна довести, аналізуючи таблицю істинності цієї функції:

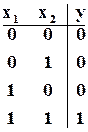
де на кожні чотири рівносторонні набори вхідних змінних 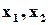(00,01,10,11) схема “відповідає” однією 1.

У відповідності із таблицею для схеми “АБО”

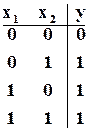
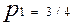та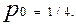

Ці прості приклади ілюструють лише саму ідею імовірнісного підходу. Для схем реальної складності можна скористатися відповідними формулами для трансформації логічних функцій в арифметичні і знайти залежності відносних частот 0 та 1 у вихідних змінних від частот 0 та 1 у вхідних змінних.

Для реалізації методу досить нескладного обладнання: генератора двійкових послідовностей із фіксованими частотами появи 0 та 1 і лічильників, які підраховують кількість 1 за задані проміжки часу. Зрозуміло, що і як будь-який статистичний метод, імовірнісне тестування вимагає використання досить довгих вхідних послідовностей, щоб забезпечити нечутливість до незначних відхилень від імовірнісних розподілів.

Але й цей метод є лише проміжним етапом в пошуку ефективних “неалгоритмічних” методів тестування. Однією із вад імовірнісного тестування виявилася невисока роздільча здатність до деяких типів несправностей. Крім того, існують несправності, які не змінюють вихідну статистику 0 та 1 і тому не можуть бути виявлені статистичними методами.

Наступним етапом в розробці і розвитку нових методів тестування, слід вважати метод, який отримав назву компактного тестування або сигнатурного аналізу. Щоб пояснити його суть і перейти до детального розгляду, почнемо трохи здалека.

Інтуїтивно зрозуміло, що, наприклад, для комп’ютера в цілому досить ефективним тестом може служити будь-яка велика (складна) програма обчислень з відомим результатом, отриманим незалежним способом. Дійсно, ймовірність того, що на несправному комп’ютері можна отримати правильний результат, який вимагає багатьох звертань до пам’яті, використання підпрограм, опцій і т. і., дуже мала. Візьмемо для прикладу таку екзотичну задачу, як комп’ютерна оркестровка музичного твору для оркестру із заданим складом інструментів. Можна напевне стверджувати, що будь-яка помилка в результаті виконання програми буде помічена вухом музиканта-професіонала. Теж саме можна сказати й про складні математичні обчислення, комп’ютерну обробку графічних матеріалів тощо.

А тепер інший приклад. Згадаймо, як здійснюється пошук несправностей в аналоговій апаратурі (підсилювачах, генераторах сигналів, телевізорах, радіоприймачах, тощо). Якщо подивитись на електричну схему такого пристрою (наприклад, фрагмент на рис. 2.13), то вона має позначки (деякі “реперні” точки), які вказують напруги, струми, вигляд осцилограм сигналів тощо (у нашому випадку - напруги).

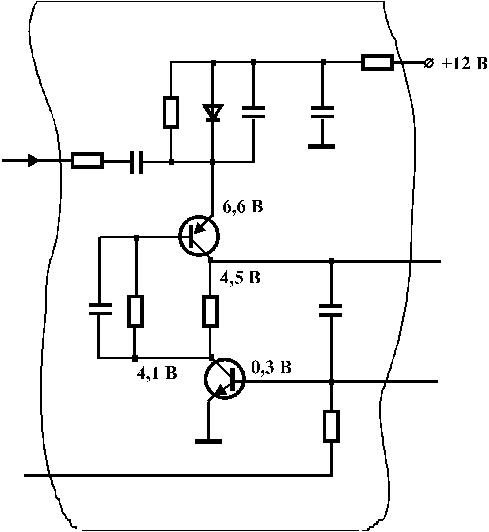
Рис. 2.13.

Що це дає при пошуку несправностей? Практично, майже все. Ремонтник, який може навіть не знати принципу роботи пристрою, перевіривши значення напруг, струмів і т.д. у контрольних точках, має можливість локалізувати несправність. Це майже напевно буде той елемент схеми, сигнали на виходах якого не відповідають нормі при нормальних, правильних значеннях вхідних сигналів. Підкреслимо найбільш суттєве з практичної точки зору: при такому підході: до кваліфікації ремонтника не висувається високих вимог. А це дуже важливо при обслуговуванні сучасної електронної техніки, враховуючи зростаючий дефіцит кваліфікованого персоналу.

Чи можна застосувати аналогічний підхід при пошуку несправностей в цифрових схемах? Безпосередньо ні, тому що в будь-якій точці схеми можна побачити і зафіксувати лише високий або низький потенціал у статичному режимі, а в динамічному – послідовності безперервних змін високого та низького потенціалів, які важко відрізнити одна від одної.

А тепер основна суть сигнатурного підходу. Будемо подавати на входи цифрового пристрою послідовність нулів та одиниць, вибрану випадково, але кожного разу одну й ту ж (тому така послідовність називається псевдовипадковою). В будь-якій точці пристрою при такому експерименті теж можна зафіксувати послідовність нулів та одиниць, яка буде залишатися однаковою при повторенні експерименту. Якщо ми будемо знати, яка послідовність відповідає справному технічному стану об’єкту, то її можна вважати ознакою того, що несправності немає, а при наявності несправності ця послідовність майже напевно буде спотворена.

Таким чином, ми й прийшли до ситуації, яка використовується для пошуку несправностей в аналогових схемах. Але залишаються ще принаймні дві проблеми, які слід розв’язати для забезпечення можливості практичного застосування такого підходу.

Перша. Вхідна псевдовипадкова послідовність повинна бути достатньо довгою для того, щоб будь - яка несправність встигла б проявити себе. Із практичного досвіду для реальних об’єктів довжина послідовності має порядок 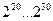, тобто десь біля 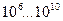біт. Можна, звичайно таку послідовність один раз вибрати, записати, наприклад, на дискету і з неї подавати на об’єкт при діагностуванні пристрою. Але так ніхто не робить. Є значно простіший і зручніший спосіб – побудувати апаратний або програмний генератор псевдовипадкових послідовностей. Як це зробити, ми розглянемо трохи згодом.

Друга проблема полягає в необхідності зафіксувати для подальшого використання ті послідовності, які виникають у контрольних точках, при проведенні діагностичного експерименту при відсутності несправностей, тобто еталонних ознак працездатності об’єкта. Довжина цих послідовностей має той же порядок, що й довжина вхідної послідовності. Тобто необхідно запам’ятати кілька десятків (по кількості контрольних точок) двійкових послідовностей кожна з яких має довжину порядку 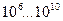біт (!). Звичайно, цю задачу розв’язати можна , але чи є необхідність фіксувати повні послідовності? Якщо замислитись, то, напевне, ні. Несправність, якщо вона проявляє себе, з великою ймовірністю спотворить більшу часину цієї послідовності, і тому можна зафіксувати, наприклад, тільки її невелику частину. Ще краще підрахувати, наприклад кількість одиниць (нулів) або кількість переходів від 0 до 1 в послідовності і зафіксувати це число, а потім порівнювати з отриманим в результаті діагностичного експерименту. Ймовірність того, що несправність спотворить вихідну послідовність так, що кількість, наприклад, одиниць в послідовності залишиться без змін, дуже мала. Все це – так би мовити, “ідеологія” сигнатурного підходу. Перейдемо до її практичного втілення.

Існує багато способів генерації псевдовипадкових послідовностей, розрахованих на апаратну або програмну реалізацію. Але найбільш популярним і поширеним є спосіб генерації за допомогою регістрів зсуву із зворотними зв’язками по модулю 2. Теорія схем цього класу існує давно, а самі схеми широко використовуються при кодуванні і декодуванні циклічних завадозахищених кодів. На рис. 2.14, а зображений 4-розрядний регістр із зворотними зв’язками, а в таблиці, яка подана разом із схемою, зведені стани цього регістру, що змінюються з кожним тактом. Повний цикл до повторення комбінації складає 15 різних двійкових слів. Якщо подивитися на таблицю по вертикалі, кожен її стовпчик – це і є псевдовипадкова двійкова послідовність, яку можна використати як тестову. Головне, що цю послідовність можна генерувати скільки завгодно раз, і вона буде залишатися тією ж самою, а кожен вихід можна з’єднати з одним із входів пристрою, на який подаються тестові впливи.

В залежності від початкового стану регістра (в нашому прикладі це 1000) будуть змінюватися і послідовності, які генеруються. Для 4-розрядного генератора таких різновидів буде 15 (табл..2.5). Вже із цього прикладу видно, що забезпечити велике різноманіття послідовностей, які генеруються, можна дуже простими апаратними засобами.

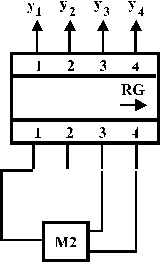
Рис. 2.14.

Таблиця 2.5.

А) б)

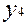
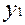
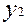
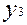
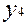
1	1	0	0	0	1	0	0	0	0
2	0	1	0	0	2	0	0	0	1
3	0	0	1	0	3	0	0	1	0
4	1	0	0	1	4	0	0	1	1
5	1	1	0	0	5	0	1	0	0
6	0	1	1	0	6	0	1	0	1
7	1	0	1	1	7	0	1	1	0
8	0	1	0	1	8	0	1	1	1
9	1	0	1	0	9	1	0	0	0
10	1	1	0	1	10	1	0	0	1
11	1	1	1	0	11	1	0	1	0
12	1	1	1	1	12	1	0	1	1
13	0	1	1	1	13	1	1	0	0
14	0	0	1	1	14	1	1	0	1
15	0	0	0	1	15	1	1	1	0
16	1	0	0	0	16	1	1	1	1

У загальному випадку зворотні зв’язки в регістрі зсуву вибираються у відповідності з деяким поліномом, який гарантує генерацію послідовностей максимальної довжини. Із теорії таких схем витікає, що цей поліном повинен бути примітивним (так само, як і для утворення циклічних кодів).

Ступінь його 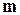відповідає довжині регістра, а довжина послідовності – 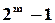. Кількість таких поліномів швидко зростає із збільшенням 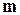і визначається функцією Ейлера

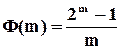
Майже в будь-якій книжці з теорії завадозахищеного кодування наведені таблиці примітивних поліномів, що дає можливість вибрати найбільш простий з них з точки зору складності схеми генератора. Здебільшого вибирають поліноми з мінімальним числом членів (доданків). У нашому прикладі був використаний поліном

.

Головна перевага такого методу формування псевдовипадкових послідовностей полягає у можливості дуже простої апаратної і програмної реалізації відповідних алгоритмів. Генератор містить лише 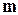-розрядний регістр зсуву і набір суматорів по модулю 2 в колі зворотного зв’язку. Сам регістр виконує функції запам’ятовування 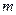- розрядної послідовності і її зсуву на один розряд праворуч. Суматори по модулю 2 в колі зворотного зв’язку обчислюють значення чергових символів, які послідовно записуються в самий лівий (молодший) розряд регістру.

Зазначимо, що, наприклад, для реалізації 32-розрядного генератора псевдовипадкових послідовностей знадобиться лише регістр відповідної розрядності та 4-5 двовходових суматори по модулю 2. При реалізації на сучасній елементній базі це лише одна ІС середнього рівня інтеграції. В той же час довжина послідовності, яка генерується таким пристроєм, складає понад 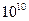32 - розрядних комбінацій.

Може виникнути питання: чому б для побудови генератора не використати звичайний двійковий лічильник? Подавши на його вхід тактові імпульси, ми теж отримаємо послідовність 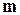-розрядних комбінацій довжиною 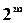. В табл. 2.5, б для порівняння показані послідовності, які генеруються лічильником. Вони мають певну регулярність, і навряд чи хто наважиться назвати їх випадковими. Можна, наприклад, побачити, що 0 і 1 в молодших розрядах розташовані через один, у другому молодшому розряді після 00 обов’язково йде комбінація 11 і т.д. Звичайно, і послідовності на виходах регістру зсуву не є випадковими, але ж їх структура (періодичність появи, наприклад, 2-х, 3-х і т.д. одиниць) змінюється. Тому можна вважати, що послідовності, які генеруються регістром зсуву із зворотними зв’язками, ближче до випадкових. Важливо також, що їх імовірністні характеристики, тобто частоти появи тих чи інших сполучень 0 і 1 можна легко змінювати відповідним вибором зворотних зв’язків регістру. До того ж різноманіття послідовностей, які генеруються регістром із зворотними зв’язками, суттєво більше, ніж кількість різних послідовностей, які можливо створити за допомогою лічильника.

Перейдемо тепер до проблеми фіксації реакцій об’єкта в контрольних точках при подачі на його входи псевдовипадкових послідовностей. Як вже зазначалось, фіксувати всю послідовність, яка виникає в певній точці схеми, недоцільно. Недоцільно передусім з точки зору складності реалізації (потрібно фіксувати послідовності занадто великої довжини), а також через велику надлишковість таких послідовностей. Тому ці послідовності бажано скоротити або, іншими словами згорнути (стиснути).

Існує безліч способів такої згортки і про деякі з них ми вже згадували. На сьогодні найбільш поширеним способом згортки є обчислення остачі від ділення полінома, що відповідає “довгій” послідовності, на поліном, суттєво “коротший” (наприклад, на той, що використовується при генерації псевдо випадкової послідовності). Саме ця остача і є сигнатурною, а метод пошуку несправностей за допомогою сигнатур отримав назву сигнатурного аналізу.

Пристрій, який здійснює обчислення остачі, називають сигнатурним аналізатором. Вперше його застосувала фірма “Hewlett-Packard” [ ]. Узагальнена схема пристрою для стиснення (згортки) послідовності 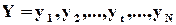має структуру, зображену на рис 2.15, і подібна до структури для генерації псевдовипадкових послідовностей (рис.2.14). Управління аналізатором здійснюється командами “Старт”, “Зсув”, “Стоп”.

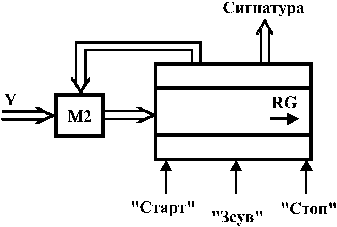
Рис. 2.15.

Сигнали “Старт” і “Стоп” формують часовий інтервал, протягом якого здійснюється процедура стиснення. Крім того, команда “Старт” встановлює початковий стан регістру, здебільшого це нульовий стан. Робота починається зі зсуву на один розряд праворуч під впливом імпульсів синхронізації “Зсув”. Після приходу кожного розряду вхідної послідовності 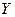обчислюється значення

,

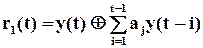де 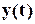- поточний символ послідовності Y, що стискається, 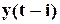– двійкові символи, які відповідають стану регістра в момент часу 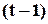, 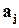- коефіцієнти полінома, які визначають зворотні зв’язки регістру. Після проходження цієї послідовності 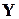в регістрі фіксується двійковий код, який і є сигнатурою

Загалом застосування сигнатурного аналізу складається із таких етапів:

- на входи еталонного (без несправностей) пристрою подається псевдовипадкова послідовність, згенерована регістром із зворотними зв’язками таким, як ми вже розглянули;

- в контрольних точках, доступних для спостереження, фіксуються і запам’ятовуються еталонні сигнатури, які в подальшому використовуються для пошуку несправностей;

- процедура пошуку полягає у перевірці відповідності реальних сигнатур еталонним. Будь-яке відхилення реально отриманої сигнатури від еталону свідчить про несправність відповідного вузла (блоку) пристрою

Наведена процедура пошуку практично не відрізняється від процедури пошуку несправностей в аналогових пристроях.Такий підхід визначає основну перевагу сигнатурного аналізу, а саме, максимальне спрощення процедури виявлення і локалізації несправностей цифрових пристроїв без застосування складної стендової апаратури і, головне, він не потребує висококваліфікованого персоналу для проведення ремонтно-відновлювальних робіт.

Прикладом, що ілюструє простоту технічної реалізації сигнатурного аналізатора, може слугувати аналізатор фірми “Hewlett-Packard”, який тривалий час був неофіційним стандартом для апаратури цього класу. Його схема складається з 16-розрядного регістру із зворотними зв’язками у відповідності з поліномом 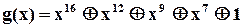та кількома логічними елементами для організації управління. Досить, мабуть лише додати, що вся ця “електроніка” разом із елементами індикації сигнатури уміщується в середині зонда (щупа), який має розміри (і вигляд) авторучки.

Як конкретний приклад реалізації сигнатурного аналізатора наведемо схему, що побудована на основі поліному 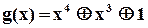(рис.2.16).

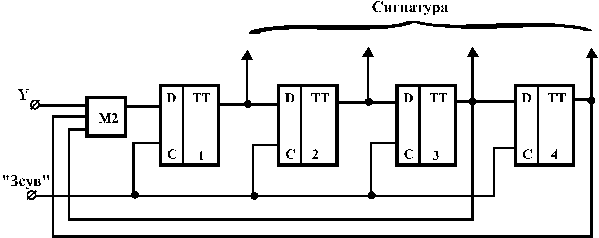
Рис. 2.16.

І на закінчення зазначимо, що при виборі і розробці конкретної схеми аналізатора застосовується модель обчислення остачі при діленні довільної двійкової послідовності, представленої відповідним поліномом, на деякий примітивний поліном 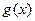. Таблиці примітивних поліномів, як вже зазначалось, можна знайти майже в будь-якій книжці з теорії завадозахищених кодів, наприклад [ ]. З точки зору спрощення технічної реалізації серед поліномів певного ступеню слід вибрати такі, що мають мінімальну кількість доданків. Наприклад, існує 7 різних примітивних поліномів ступеня 16,

; ;

; ;

; ;

,

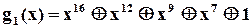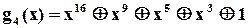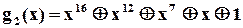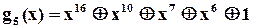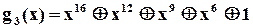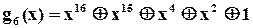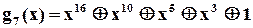які мають по 5 доданків. Один з них і вибрали автори із “Hewlett-Packard” для побудови свого аналізатора.

Контрольні питання.

1.В чому полягає ймовірністний підхід до контролю цифрових пристроїв?

2.Що означає термін “псевдовипадкова послідовність”?

3.Що таке “сигнатура”?

4.Які етапи застосування сигнатурного аналізу?

5.Яка аппаратура використовується на практиці для сигнатурного аналізу?

ЛІТЕРАТУРА

1. Дж. фон Нейман, Вероятностная логика и синтез надёжных организмов из ненадёжных компонент, в сб.»Автоматы» под ред. К.Шеннона и Дж. Маккарти, «Ин. Литература», М., 1956, с.68–139

2. А.Авиженис, Гарантоспособные вычисления : От идей до реализации в проектах, Тематический выпуск ТИИЭР «Отказоустойчивость в СБИС», т.74, 1986, с.8-21

3. Липаев В.В. Надежность программных средств, Издательство СИНТЕГ, Москва, 1998, 232с.

4. Савченко Ю.Г. Цифровые устройства, нечувствительные к неисправностям элементов. – М. : Сов. Радио, 1976, с.218

5. Иыуду К.А. Надёжность, контроль и диагностика вычислительных машин и систем. – М. Высшая школа, 1989. – с.215

6. Рижук М.П., Савченко Ю.Г. Інформаційна надлишковість як універсальний засіб контролю реальних об’єктів // Вимірювальна та обчислювальна техніка в технологічних процесах. – Хмельницький: ТУП. –2001. – N1, C.90–2.

7. Харченко В.С. Теоретические основы дефектоустойчивых цифровых систем с версионной избыточностью.– Харьков: Изд–во ХВУ, 1996.– 506 с.

8. Хетагуров Я.А. Основы построения управляющих вычислительных систем.– М.: Радио и связь, 1991.– 228 с.

9. Чернышев А.А. Основы конструирования и надежности электронных вычислительных средств.– М.: Радио и связь, 1998.– 448 с.

10. Тейер Т., Липов М., Нельсон Э. Надежность программного обеспечения.– М.: Мир, 1981.– 323 с.

11. Гласс Р. Руководство по надежному программированию.– М.: Финансы и статистика, 1982.– 256 с.

12. Аджиев В. Мифы о безопасном ПО: уроки знаменитых катастроф // Открытые Системы.– 1999.– № 6.– С. 3–23.

▲ ▼ ▲