2. 3. Кодові методи функціонального контролю

Дата: 2025-05-21; Просмотры: 4

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Спочатку розглянемо традиційну схему використання завадозахищених кодів в системах зв’язку (рис. 2.8).

Рис. 2.8.

У повідомлення, які генеруються джерелом, за допомогою кодера повідомлень додається деяка кількість надлишкових (перевірочних) розрядів, які забезпечують можливість виявлення або (і) виправлення помилок. Кодове слово 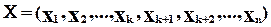надходить до кодера каналу (наприклад, модуляція радіочастотою). Сформовані таким чином сигнали передаються по каналу, в якому діють завади, що може причинити спотворення сигналів. Після отримання повідомлення декодер каналу проводить зворотне перетворення сигналів на електричному рівні (наприклад, демодуляцію), після чого у повідомленні виявляються або (і) виправляються помилки декодером отримувача. У цій схемі нас насамперед будуть цікавити функції кодера повідомлень і декодера отримувача, які ще майже не пов’язані із електричними трансформаціями сигналів.

У наведеній схемі канал передачі інформації (телефонна лінія, коаксіальний кабель, радіоканал, оптоволокно тощо) не змінює кодове слово 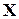, якщо не враховувати впливу завад. Тому корегуючи властивості, закладені у повідомлення при кодуванні, не змінюються (кодова відстань між окремими словами, саме яка забезпечує можливість корекції, залишається незмінною).

Інша справа, коли ми за цією ж схемою спробуємо використати завадозахищені коди в цифрових пристроях. Виявиться, що кодове слово після проходження через практично будь-яку цифрову схему зміниться так, що закладені при кодуванні корегуючи властивості зникнуть або зміняться.(передусім, порушаться кодові відстані між словами).

Тому для контролю і корекції помилок на виходах цифрових пристроїв застосовується інша схема (рис. 2.9, а) [ ], яка узагальнює більшість розглянутих раніше методів. Так, наприклад, схема апаратного самоконтролю із порівнянням виходів (рис. 2.9,б) та мажоритарне відновлення сигналів (рис. 2.9, в) можуть бути представлені цією універсальною структурою. Відмінність полягає лише в класі завадозахищених кодів, які використовуються: для функціонального контролю – коди з виявленням помилок; для створення пристроїв, нечутливих до відмов компонентів – коди з виправленням помилок. Саме тому кодовий підхід можна вважати найбільш загальним. Його цінність полягає передусім у можливості варіації в широких межах повноти контролю або рівня надійності шляхом вибору відповідних кодів (з більшою, чи меншою корегуючою здатністю).

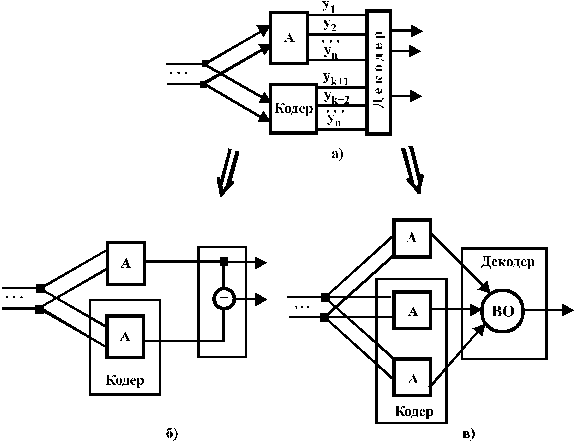
Рис. 2.9.

Перед тим, як перейти до аналізу загальних властивостей методу, розглянемо кілька простих прикладів. Для спрощення будемо вважати, що вихідний пристрій, до якого застосовується кодовий метод, є комбінаційною схемою і реалізує такі функції:

;

;

;

.

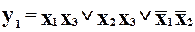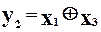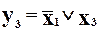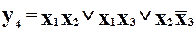Для функціонального контролю виберемо найпростіший код із однією перевіркою на парність, який виявляє всі помилки непарної кратності. Для цього, як ми вже знаємо, потрібно додати один перевірочний розряд із рівняннями кодування

.

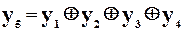Підставивши значення інформаційних розрядів із (?), отримаємо

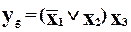- це функція, яку повинен реалізувати кодер.

Як бачимо, складність цієї функції суттєво менша за складність контрольованої схеми.Власне контроль відбувається у декодері, функція якого полягає в підрахунку парності кількості одиниць у кодовому слові .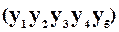

Можна вибрати й інший код. Наприклад, коли перевірочний розряд 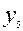утворити відповідно до функції 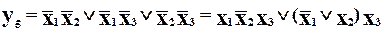, то отримаємо “ваговий” код ”3 із 5”, дозволені кодові комбінації якого містять рівно 3 одиниці із п’яти розрядів (табл. 2.2)

Таблиця 2.2.

До речі, цей код, як і попередній, виявляє досить велику частину всіх можливих помилок. Відповідно з (1.18) отримаємо

,

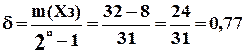тобто 77% помилок, які теоретично можуть виникнути на виходах контрольованого пристрою, виявляється.

Розглянемо тепер випадок виправлення помилок, для чого застосуємо код Хемінга з 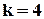інформаційними розрядами і, 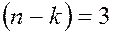перевірочними, які задаються рівняннями кодування

;

;

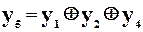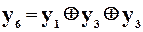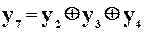
Зробивши аналогічну підстановку, отримаємо

;

;

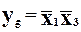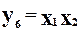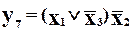
Це ті функції, які реалізує кодер. Декодування проводиться за стандартними процедурами, які ми вже розглянули.

Якщо у нас виникне потреба посилити корегуючи здатність контролю, можна збільшити кількість перевірочних розрядів, додавши, наприклад, ще один 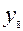як суму по модулю 2 всіх вихідних сигналів схеми, тобто

.

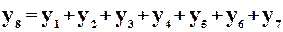Знову, зробивши відповідну підстановку, отримаємо

.

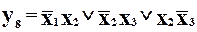В результаті отримаємо схему, в якій можна не тільки виправляти однократні помилки, але й виявляти двократн Розглянувши наведені приклади, звернемо увагу на таке.

У всіх випадках складність кодера не перевищує складності вихідного пристрою. У порівнянні з мажоритарним методом це можна вважати суттєвим виграшем, але при цьому ми зменшили корегуючи здатність до виправлення лише однократних помилок.

По-друге, для корекції можна було б вибрати інший код з іншими рівняннями кодування або іншою корегуючою здатністю. Ця властивість кодового підходу є найбільш важливою з точки зору можливості оптимізації за критеріями мінімуму апаратних витрат або максимуму корегуючої здатності, що створює сприятливі умови для пошуку компромісних схемних рішень, тобто таких, при яких задані вимоги до надійності забезпечуються мінімальними апаратними витратами.

Зрозуміло, що наведені приклади є занадто простими, для того щоб робити висновки загального характеру. Проте накопичений досвід розробки високонадійної цифрової апаратури показує, що саме на основі кодових методів можна забезпечити бажану селективність і керованість введення надлишковості.

Чому це важливо? У випадках комп’ютерного управління реальними об’єктами (а саме у цих випадках виникає проблема забезпечення надійності) окремі помилки можуть бути найбільш небезпечними і навіть неприпустимими в жодному разі. Уявімо собі, що ви піднімаєтесь ліфтом, а ті “ігреки” 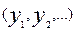– команди на пуск маршового двигуна, відкриття (закриття) дверей і т.і. Із вимог безпеки ясно, це неприпустиме одночасне відкриття дверей кабіни і пуск двигуна, що рухає кабіну. І саме така помилка повинна бути принаймні виявлена, хоча б з тим, щоб заблокувати виконання відповідних команд. Інші помилки не є такими небезпечними і не обов’язково їх виявляти і, тим більше виправляти. І це зрозуміло: все, що безпосередньо не загрожує життю людини можна вважати вторинним. Зрозуміло також, що всі наявні ресурси (надлишковість – це зайві витрати) повинні бути спрямовані саме на найбільш небезпечні помилки. Тому кодовий підхід, який надає можливість цілеспрямованого введення надлишковості і, як ми з’ясували, узагальнює більшість інших підходів, є найбільш універсальним.

А тепер щодо співставлення класичних методів (мажоритарного, функціонального контролю за схемою рис. 2.2. та ін.) з кодовим. Із загальнотеоретичних позицій принципової різниці між ними немає, справа тільки в тому, які коди застосовуються. У першому випадку (мажоритарний метод та ін.) – коди з повторенням, які мають потужну корегуючи здатність і, відповідно, вимагають великої надлишковості, у другому – коди з меншою корегуючою здатністю, але й з меншою надлишковістю. Який метод вибрати для конкретного пристрою, залежить від вимог до надійності та наявних ресурсів (припустимих габаритів, ваги і, нарешті, вартості).

Загалом можна стверджувати (про це свідчить накопичений досвід), що у випадках виявлення всіх можливих помилок на виходах пристрою необхідні апаратні витрати знаходяться на рівні подвоїння, а для виправлення (нейтралізації) всіх можливих помилок – потроїння. Зменшення цих витрат можливе лише за рахунок зниження корегуючою здатності і, як наслідок, надійності. Як говорять фахівці з надійності: “За надійність потрібно платити, а за ненадійність доводиться розплачуватися”.

Проте слід зазначити, що реальні апаратні витрати в значній мірі залежать від специфіки конкретного пристрою, до якого застосовуються методи забезпечення надійності, елементної бази та інших, суто технічних факторів.

Контрольні питання

1.Чому для цифрових пристроїв не може бути застосована класична схема корекції помилок на основі завадозахищених кодів?

2. Чому кодовий підхід можна вважати універсальним і узагальнюючим?

3. Які апаратні витрати необхідні для виявлення і корекції помилок на виходах цифрового пристрою?

4. Яким чином забезпечується селективність по відношенню до помилок, які корегуються?

2.4. ТЕСТОВИЙ КОНТРОЛЬ

Нагадаємо про основну відміну тестового контролю від функціонального: тестування здійснюється у спеціальному режимі, коли об’єкт не виконує своїх робочих функцій, і метою тестування є не виявлення (виправлення) помилок, а визначення технічного стану об’єкту. Результатом тестування є висновок типу: “Об’єкт працездатний/непрацездатний”, “в об’єкті несправний блок (модуль) №...”. Найбільш суттєвою є відмінність кінцевої мети контролю: при функціональному визначається правильність виконання об’єктом в даний момент своїх функцій, при тестовому – наявність чи відсутність несправностей.

Чому ця відміна є принциповою? Справа в тім, що визначення технічного стану об’єкту на основі перевірки правильності виконання ним своїх функцій для більшості цифрових пристроїв практично не може бути реалізовано. Для прикладу уявімо собі, що потрібно перевірити правильність виконання функції складання звичайним калькулятором. Для цього, строго кажучи, ми повинні складати по черзі всі можливі доданки, наприклад, довжиною 8 десяткових розрядів. Це означає, що нам потрібно виконати 10¹⁶ додавань тільки для того, щоб на 100% переконатися в правильності виконання калькулятором тільки функції складання.

Нескладний підрахунок показує, що якщо на кожне складання ми будемо витрачати 1 сек., то вся перевірка займе 3´10⁸ років (!). Зрозуміло, що цей приклад трохи штучний, адже перевірку можна проводити і в автоматичному режимі. Тоді при швидкості в 10⁸ операцій/сек перевірка буде проведена лише за 3 сек. Але ж це тільки функція складання, а об’єкт перевірки – лише простий калькулятор.

А що робити, коли необхідно протестувати сучасний комп’ютер або комп’ютерну мережу? Основна “ідеологія” тестового підходу полягає в переході від перевірки функцій до перевірки технічного стану обладнання, тобто наявності чи відсутності несправностей.

Перед тим, як перейти до методів побудови тестів, з’ясуємо вплив наявності несправності на функції цифрового пристрою. Розглянемо спочатку прості приклади. На рис. 2.10 показана вентильна реалізація схеми “І” (а – справної схеми, б –схеми, в якій в колі змінної стався обрив). Як бачимо із таблиці 2.3, несправність змінює функцію, яку реалізує схема.

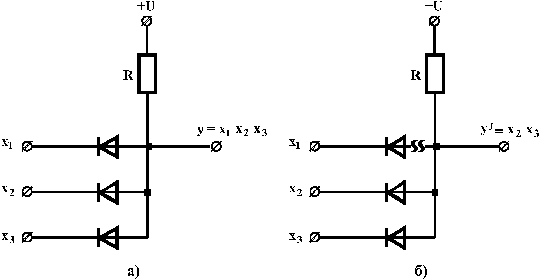
Рис. 2.10.

Таблиця 2.3.

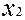
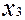
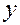
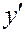
0	0	0	0	0
0	0	1	0	0
0	1	0	0	0
0	1	1	0	1
1	0	0	0	0
1	0	1	0	0
1	0	1	0	0
1	1	1	1	1

Як виявити саме цю несправність, не перебираючи на входах всі вісім наборів перемінних? Очевидно, досить подати набір 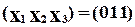і, якщо 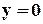, то цієї конкретної несправності (обриву по 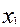) немає, а якщо 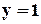, то є. Набір 011 – це тест, який виявляє задану несправність. Такий тест називають перевіряючим (або контролюючим).

Розглянемо тепер аналогічний приклад для схеми “АБО” (рис.2.11 та табл. 2.4).

Для цієї схеми і для заданої несправності (обрив в колі 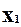) перевіряючим тестом буде набір (100). Для інших несправностей із фізичних та інтуїтивних міркувань неважко знайти відповідні тестові набори, а потім об’єднати їх в одну тестову послідовність (до речі, цю послідовність здебільшого називають тестом). У більшості випадків один тестовий набір виявляє більше, ніж одну несправність, тому довжина загальної тестової послідовності (тесту) практично завжди значно менше суми тестових наборів.

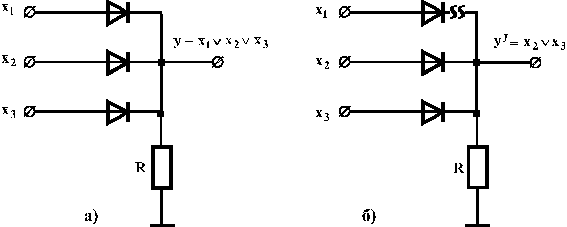
Рис. 2.11.

Таблиця 2.4.

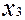
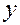
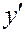
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	1	1
1	0	0	1	0
1	0	1	1	1
1	1	0	1	1
1	1	1	1	1

У загальному випадку перевіряючим тестом для заданої несправності 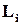називається такий вхідний вплив, що вихідна реакція об’єкту на нього різна при наявності і відсутності .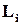