Виправлення (корекція) помилок.
Очевидно, якщо код повинен виправляти сукупність помилок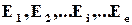 
, то всі відповідні цим помилкам синдроми повинні бути різними, тобто відповідність 
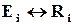має бути взаємно однозначною. Тільки в цьому випадку ми зможемо за значенням синдрому знайти відповідний йому вектор помилки і виправити помилку. З цього зокрема витікає, що перевірочна матриця коду, який виправляє всі однократні помилки, повинна мати n різних ненульових стовпців. Зокрема матриця, в якій стовпці пробігають всі ненульові значення 
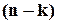-розрядних чисел
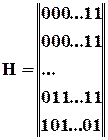(2.14)
може бути використана як перевірочна коду, який виправляє всі однократні помилки. Така матриця відрізняється від канонічної форми
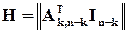(2.15)
лише розташуванням стовпців. Якщо стовпці, які містять по одній одиниці, перенести праворуч і сформувати з них одиничну матрицю, то ми отримаємо саме форму (2.14). Слід зазначити, що така процедура еквівалентна лише перенумерації позицій символів і не є принциповою з точки зору властивостей коду.
Форма матриці (2.14) є цікавою з іншого погляду. По-перше, саме у такому вигляді були запропоновані Хемінгом перші коди із корекцією помилок. По-друге, при використанні такої матриці синдром безпосередньо у двійковому вигляді вказує номер розряду, який спотворено:
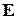
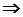
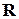
100...00 00...01
010...00 00...10
001...00 00...11
... ...
000...01 11...11
У кодах Хемінга додаткові (перевірочні) розряди займають 1, 2, 8,...,2n-k позиції. З точки зору матричного представлення це не дуже зручно, але з технічної – не викликає жодних додаткових проблем.
Хемінгом були запропоновані (1948р.) три класи кодів.
1. Уже розглянутий нами код з однією перевіркою на парність. Для нього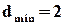 
і він виявляє всі помилки непарної кратності. Для нього 
.
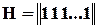2. Коди з виправленням однократних помилок з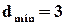 
. Це ряд кодів, для яких
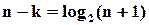(2.16)
Наприклад, код з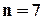 
і 
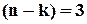
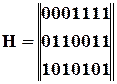
1234567
Із перевірочної матриці можна викреслити деяку кількість стовпців і це не зменшить корегуючої здатності кода. Головне – не зменшувати кількість перевірочних розрядів. Такі коди (отримані шляхом викреслення деякої кількості стовпців із повної матриці) називають укороченими.
3. Ще один клас кодів Хемінга з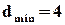 
. Ці коди дозволяють виявляти помилки кратності 
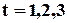, або виправляти помилки кратності 
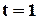та виявляти помилки кратності 
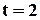. Саме у цьому варіанті такі коди найчастіше і використовують.
Щоб отримати код з 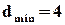, досить перевірочну матрицю 
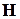коду з 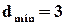доповнити ще одним рядком з одиниць:
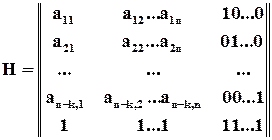
Цьому додатковому рядку відповідає ще один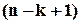 
-ий додатковий розряд і ще одне рівняння перевірки
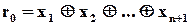
Таким чином, при декодуванні ми отримуємо 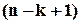результатів перевірки
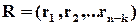та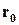 
.
Другий етап декодування коду базується на аналізі результатів перевірки. Вони можуть бути такими:
а)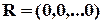 
; 
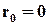– помилок немає;
б)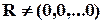 
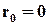; – однократна помилка, яка може бути виправлена на основі відповідності 
;
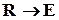в) 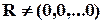; r0 = 0 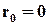– 2-кратна помилка, яка лише виявляється, але не може бути виправлена.
Таким чином, ми маємо універсальний метод побудови кодів з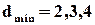 
, які, відповідно, виявляють однократні помилки, виправляють однократні та виявляють 2-кратні.
Для інших випадків не існує універсальних методів, тобто придатних для довільних значень 
або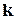 
, побудови кодів. В узагальненому вигляді задача побудови коду формулюється так.
Задана сукупність векторів помилок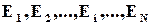 
. Необхідно знайти таку перевірочну матрицю 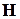, для якої всі добутки 
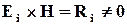для випадку виявлення заданої сукупності помилок та додатково у випадку їх виправлення всі синдроми повинні бути різними, тобто
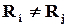для всіх 
.
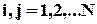В принципі не існує іншого алгоритму, крім прямого перебору, побудови кодів, що корегують (виявляють або виправляють) довільну сукупність помилок. При виконанні такого перебору може виявитися корисною така властивість: якщо вектору помилки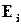 
відповідає синдром 
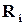, а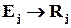 
, то вектору помилки
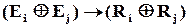(2.17)
(ця властивість є наслідком лінійності всіх операцій, які застосовуються у теорії кодування).
Задача аналізу кодів, що виправляють помилки, досить складна тому, що потрібно аналізувати не окремі вектори помилки, а їх повну сукупність: всі синдроми, що відповідають такій сукупності, повинні бути різними. Як цього досягти для однократних помилок, ми вже розглянули. Для деяких інших сукупностей – розглянемо в наступному розділі в рамках циклічних кодів.
Циклічні коди. Насамперед зауважимо, що циклічні коди є підкласом групових кодів, тобто циклічні коди теж групові, але мають свою специфіку головним чином щодо математичного апарату та символіки, які використовуються для їх побудови та аналізу. В терміналах абстрактної алгебри циклічний код – це кільце, тобто така замкнена сукупність елементів, для яких задані дві операції та обернені до них. Зокрема, в нашому випадку це порозрядне додавання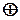 
(обернена операція співпадає із самою операцією) та множення (зворотна – ділення). Самі елементи – двійкові -розрядні комбінації – записуються як поліноми. Правило, за яким встановлюється відповідність, можна пояснити прикладом:
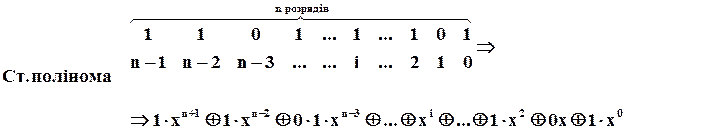
Більш компактно цей поліном можна записати так:
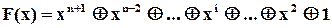
Такі поліноми можна додавати, множити і ділити за звичайними правилами з урахуванням специфіки операції суми по модулю 2, а саме
; 
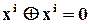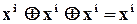
Наприклад,
а)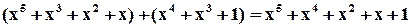 
б)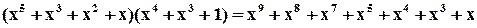 
в)
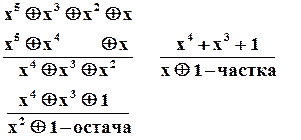
Можна дати таке (спрощене) визначення циклічного коду.
Циклічний код утворює множина дозволених кодових комбінацій, відповідні яким поліноми без остачі діляться на деякий поліном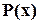 
, який називають породжуючим. (Аналогія: множина чисел, які без остачі діляться на деяке число 
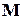Наприклад, всі числа кратні 2 (парні числа), або 3 чи іншому числу).
Існує два способи утворення циклічного коду, точніше, дозволених кодових комбінацій.
1. Множенням довільної 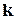-розрядної комбінації у вигляді відповідного їй полінома 
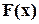ступені 
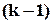на породжуючий поліном 
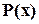. У цьому випадку кодове слово може бути представлене як
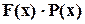
і, очевидно, воно завжди без остачі ділиться на .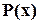
Такий спосіб з математичної точки зору є найбільш простим і прозорим, але на практиці застосовується дуже рідко. Причина полягає в тому, що в цьому випадку ми отримуємо несистематичний (нерозділимий) код – інформаційна частина 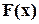у кодовій комбінації не зберігається (в результаті множення вона “змішується” з 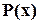). Це суттєво ускладнює процедуру декодування при наявності помилок.
2. Дописуванням до 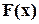з боку молодших розрядів остачі 
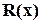від ділення 
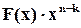на породжуючий поліном 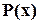. (Зазначимо, що множення на 
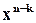означає просте дописування до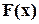 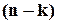нулів.) Формально це можна записати так
.
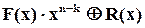Неважко переконати, що отриманий таким чином поліном завжди буде без остачі ділитися на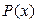 
.
Як підкреслювалось на самому початку, циклічні коди є підкласом групових кодів, тобто будь який циклічний код може бути заданий також відповідно породжуючою матрицею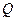 
. Для цього досить знайти остачі для перших 
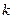рядків одиничної матриці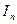 
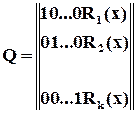
Не будемо забувати, що рядки матриці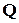 
– це насамперед кодові слова в вони можуть бути утворені за звичайними правилами. Утворимо їх для прикладу конкретного кода з 
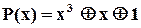і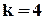 
.
Рядки одиничної матриці і відповідні операції:
; 
; 
; 
; 
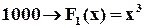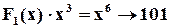
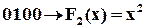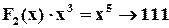
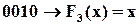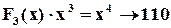
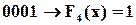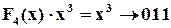
Таким чином, породжую чому поліному 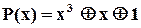для кода з 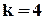інформаційними розрядами відповідає породжуюча матриця
.
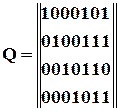Циклічний код з 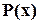і груповий код з 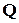еквівалентні. Крім того, як неважко переконатися, обчислення остачі 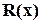еквівалентно обчисленню синдрому 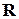в групових кодах. Зауважимо також, що відповідність між груповими і циклічними кодами не є взаємною: будь-якому циклічному коду можна знайти еквівалентний груповий код, але не навпаки. Клас групових кодів значно ширший, ніж клас циклічних кодів.
Основні циклічні коди. На практиці саме циклічні коди використовуються найчастіше. Це пояснюється їх простою схемною реалізацією на регістрах зсуву із зворотними зв’язками та простим математичним апаратом, за допомогою якого можна описати циклічні коди та проаналізувати їх корегуючу здатність.
Для побудови циклічних кодів найчастіше використовуються так звані неприводимі поліноми (аналог – прості числа). Із теорії кодування відомо, що далеко не всі неприводимі поліноми придатні для побудови ефективних кодів. Так, для отримання максимального числа різних остач при декодуванні породжуючий поліном 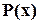повинен бути дільником 
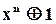. Таблиці неприводимих дільників для різних значень 
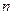наводяться у більшості книжок з теорії кодування. Не заглиблюючись в дебрі теорії, приймемо цю вимогу на віру і розглянемо деякі конкретні коди.
1. Код з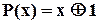 
ми вже фактично розглянули. Цей код забезпечує 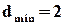і дозволяє виявляти всі однократні помилки, а також всі помилки непарної кратності. Це легко довести, аналізуючи подільність полінома, що відповідає вектору помилки 
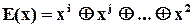(кількість доданків непарна), на .
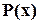2. Код з 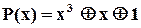. Цей поліном неприводимий і є дільником 
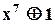, тому існує код з 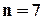та 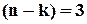. Код з такими параметрами дає 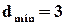, тому він спроможний виправляти однократні помилки або виявляти двократні. Такі самі характеристики має код з 
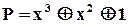. Із таблиць можемо знайти інші поліноми для інших значень та 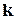. Наприклад,
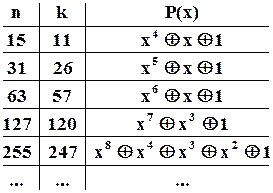
Всі ці коди оптимальні (довершені) і є аналогами уже розглянутих нами кодів Хемінга. В таблиці наведено лише по одному поліному для кожного значення та 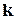(насправді може бути по кілька еквівалентних варіантів).
2. Код з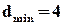 
для виправлення однократних і виявлення двократних помилок. Такі коди отримують із попередніх домноженням 
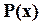на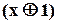 
. При домноженні кількість перевірочних розрядів і, відповідно довжина кодових слів збільшується на 1. Наприклад, з (31,26) – коду отримаємо (32,26) – код із породжуючим поліномом.
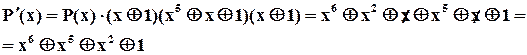
Цей код виправляє однократні та виявляє двократні помилки у 32 – розрядних двоїчних словах. Процедура декодування аналогічна відповідній процедурі для кодів Хемінга з 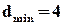. Ознакою двократної помилки у цьому випадку буде неподільність прийнятої комбінації на 
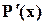і подільність на .
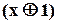Коди БЧХ. Ці коди отримали свою назву від прізвищ їх авторів (Р. Боуз, Д. Рой-Чаудхурі та А. Хоквінгем). Коди БЧХ є узагальненням кодів Хемінга і дозволяють виправляти кратні помилки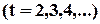 
. Не заглиблюючись в теорію кодів БЧХ, зазначимо, що породжуючий поліном для цих кодів утворюється як найменше загальне кратне деякої сукупності непрводимих поліномів (у більшості випадків – це добуток поліномів). Деякі з кодів БЧХ наведені у таблиці 2.1.
Таблиця 2.1
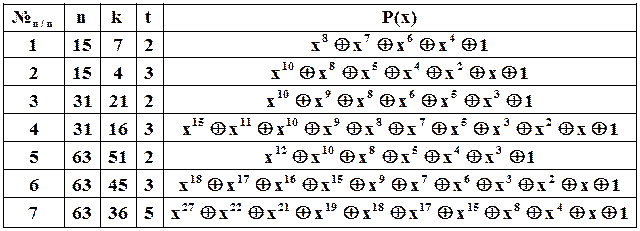
Контрольні питання
1. Що таке корегуюча здатність завадозахищеного кода? Чим вона визначається?
2. Що спільного і чим відрізняються між собою групові та циклічні коди?
3. Яку має структуру породжуючи матриця коду?
4. Які способи утворення циклічних кодів?
5. Що таке неприводимі поліноми?
6. У чому полягає процедура декодування циклічних кодів?
7. У чому полягає основний спосіб утворення БЧХ – кодів?