Очевидно також, що помилка в повідомленні може бути виявлена тоді і тільки тоді, коли вона перетворює дозволене слово в заборонене.
Для кожного дозволеного слова таких різних помилок може бути рівно 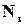 , а максимальна кількість всіх можливих помилок при заданому способі двійкового кодування
, а максимальна кількість всіх можливих помилок при заданому способі двійкового кодування
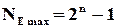 ,
,
де 1 записана в рахунок випадку, коли помилок немає. Відносну кількість (“долю”) помилок, яку можна виявити при заданому способі кодування, обчислимо як
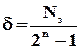 . (2.5)
. (2.5)
Обчислимо 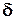 для таких випадків.
для таких випадків.
1. Код із однією перевіркою на парність.
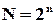 ;
; 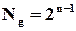 (дозволені слова мають парну кількість одиниць – їх рівно половина).
(дозволені слова мають парну кількість одиниць – їх рівно половина).
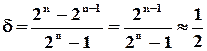 (50%)
(50%)
2. Код, що має два додаткових розрядів (код із контролем по модулю 3)
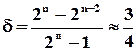 (75%) .
(75%) .
3. Код із “повторенням“. Кожне слово передається джерелом двічі. Тоді
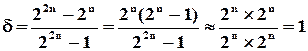 (100%)
(100%)
З цих прикладів бачимо, що здатність коду до виявлення помилок зростає дуже швидко із зростанням надлишковості. Зауважимо також, що формула (2.5) є універсальною в тому розумінні, що оцінка здатності до виявлення помилок не залежить від способу кодування інформації.
У класичній теорії кодування застосовується дещо інший підхід. Він базується на визначенні кодової відстані та понятті кратності помилки 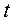 . При двійковому кодуванні:
. При двійковому кодуванні:
– кодова відстань 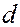 d
d 
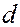 між двома словами – це кількість розрядів, якими відрізняється одне слово від другого;
між двома словами – це кількість розрядів, якими відрізняється одне слово від другого;
– кратність помилки .t – це кількість розрядів, які спотворені помилкою;
– вектор помилки E =( e 1 , e 2 ,…., en ) .– це двійкова комбінація, яка містить 1 в тих розрядах слова, які спотворені.
Таким чином, кратність помилки – це “вага” вектора помилки – кількість одиниць в ньому.
Легко довести, що мінімальна кодова відстань для виявлення помилок кратності 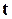 і менше повинна бути
і менше повинна бути
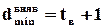 (2.6)
(2.6)
При виконанні (2.6) жодна помилка кратності 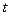 і менше не зможе перетворити одне дозволене слово в інше також дозволене слово).
і менше не зможе перетворити одне дозволене слово в інше також дозволене слово).
Очевидно, формули (2.5) і (2.6) у конкретних випадках мають бути еквівалентні. Спробуємо це показати. Візьмемо знову код із однією перевіркою на парність. Додавши один розряд таким чином, щоб кількість одиниць у слові стала парною, ми “розносимо” слова на 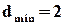 (до цього було
(до цього було 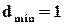 ). Зразу ж можна стверджувати, що будь-яка однократна помилка у цьому випадку буде виявлятися, бо вона перетворює слово із парною кількістю одиниць у слово із непарною кількістю. А які інші помилки будуть виявлятися? Очевидно, всі ті, для яких
). Зразу ж можна стверджувати, що будь-яка однократна помилка у цьому випадку буде виявлятися, бо вона перетворює слово із парною кількістю одиниць у слово із непарною кількістю. А які інші помилки будуть виявлятися? Очевидно, всі ті, для яких 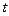 непарне. А всього таких помилок буде приблизно половина (50%). В інших випадках потрібен детальний аналіз конкретних помилок, які виявляються і які не виявляються.
непарне. А всього таких помилок буде приблизно половина (50%). В інших випадках потрібен детальний аналіз конкретних помилок, які виявляються і які не виявляються.
А тепер про більш складний випадок – виправлення помилок. Яка для цього потрібна надлишковість? І найголовніше, що потрібно для того, щоб помилку можна було не тільки виявити але й виправити? Очевидно, попередня умова,виконання якої необхідне для виявлення помилок, залишається справедливою і для їх виправлення: помилка повинна перетворювати дозволене слово в заборонене. Але цього не досить. Якщо два чи більше дозволених слова можуть переходити в одне заборонене, то, отримавши це слово замість дозволеного (без помилок), у отримувача не буде підстав, щоб надати перевагу будь-якій із гіпотез щодо того, яке саме дозволене слово було спотворено завадою. Що ж потрібно для того, щоб можна було таку первагу віддати? Очевидно, для надання такої переваги ймовірності помилок повинні бути суттєво різними. Тоді, отримавши заборонене слово, будемо мати підстави віддати перевагу тій помилці, яка має найбільшу ймовірність. Але де взяти ці ймовірності? В реальних випадках вони не можуть вважатися відомими.
В теорії завадостійкого кодування вважається (і це може бути обґрунтовано теорією ймовірностей),що для незалежних помилок ймовірність виникнення помилки дуже швидко зменшується із зростанням її кратності, тобто найбільш ймовірні однократні помилки, менш ймовірні 2-кратні помилки і так далі.
У будь-якому випадку множина можливих помилок завжди має бути обмежена або конкретною кратністю, або конкретним переліком. Якщо таке обмеження виконано, (а це обов’язково треба зробити), то достатню умову для можливості виправлення помилок можна сформулювати так: кожна з помилок, яка має бути виправлена, повинна переводити кожне із дозволених слів не більше, ніж в одне заборонене слово.
Таким чином, кожному дозволеному слову треба мати можливість співставити не менше, ніж 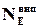 заборонених слів, звідси безпосередньо витікає, що
заборонених слів, звідси безпосередньо витікає, що
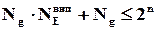 ,
,
або 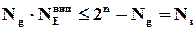 , звідки
, звідки
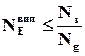 (2.7)
(2.7)
Для виправлення помилок певної кратності (частковий випадок) корегуючу здатність можна визначити через мінімальну кодову відстань
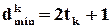 (2.8).
(2.8).
Групові коди. Із попереднього матеріалу може скластися враження, що знаючи співвідношення (2.6) та (2.8), легко побудувати будь-який код. Наприклад, для цього, здавалось би, досить “рознести” дозволені слова на відповідну мінімальну відстань, і задачу можна вважати розв’язаною. Але це лише на перший погляд. Дійсно, коли треба знайти, наприклад, тільки кілька сотень дозволених слів ( 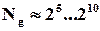 ), то за допомогою комп’ютера це можна зробити, мабуть, за кілька хвилин. В результаті будемо мати таблицю дозволених слів, яку можна використати при декодуванні (виявленню або виправленню помилок). А що коли
), то за допомогою комп’ютера це можна зробити, мабуть, за кілька хвилин. В результаті будемо мати таблицю дозволених слів, яку можна використати при декодуванні (виявленню або виправленню помилок). А що коли 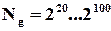 або ще більше? Де зберігати таку таблицю, якщо її навіть вдасться побудувати? (На це потрібно витратити далеко не хвилини і навіть не години комп’ютерного часу, бо задача має комбінаторний характер).
або ще більше? Де зберігати таку таблицю, якщо її навіть вдасться побудувати? (На це потрібно витратити далеко не хвилини і навіть не години комп’ютерного часу, бо задача має комбінаторний характер).
Головна мета класичної теорії кодування полягає у створенні конструктивних процедур кодування і декодування, які мають прості апаратні або програмні реалізації. Теорія кодування вивчає головним чином так звані групові коди. Ця назва походить від поняття група з вищої алгебри.
Група – це замкнена відносно групової операції сукупність об’єктів. Група обов’язково містить також елемент, який називають одиничним або нульовим в залежності від того, яка використовується групова операція. Поняття замкненості полягає в тому, що застосування групової операції до двох чи більше елементів групи дає в результаті також елемент групи, а групова операція між будь-яким елементом групи і одиничним (нульовим) елементом дає в результаті сам елемент.
Все це – визначення на абстрактному рівні, і, мабуть, не зовсім зрозуміло, про що йде мова. Наведемо прості приклади, які зроблять ці визначення прозорими.
Всі дійсні числа – група відносно операції додавання ( 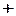 ) із нульовим елементом 0. Складаючи дійсні числа, ми завжди отримуємо теж дійсні числа (замкненість), а додавши 0 до будь-якого числа, ми отримуємо теж саме число. Відносно операції множення (
) із нульовим елементом 0. Складаючи дійсні числа, ми завжди отримуємо теж дійсні числа (замкненість), а додавши 0 до будь-якого числа, ми отримуємо теж саме число. Відносно операції множення ( 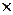 ) з одиничним елементом 1 теж отримаємо замкнену групу. Інший приклад: числа, які без остачі діляться на 3. Складаючи або перемножуючи такі числа, ми отримуємо числа, які без остачі діляться на 3. Можна навести і інші численні приклади.
) з одиничним елементом 1 теж отримаємо замкнену групу. Інший приклад: числа, які без остачі діляться на 3. Складаючи або перемножуючи такі числа, ми отримуємо числа, які без остачі діляться на 3. Можна навести і інші численні приклади.
В теорії кодування двійкові  -розрядні слова
-розрядні слова 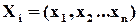 – це група відносно операції порозрядного додавання по модулю 2 (
– це група відносно операції порозрядного додавання по модулю 2 ( 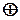 ), а нульовий елемент – кодове слово
), а нульовий елемент – кодове слово 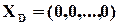 .
.
Саме по собі таке визначення поки нічого не дає – проблема компактного представлення множини кодових слів зберігається. Але з математики відомо, що група може бути представлена своїм базисом. Базис – це мінімальна сукупність незалежних елементів, застосовуючи до яких групову операцію (до різних сполучень елементів базису), можна відтворити всю групу.
Наприклад,
Базис: 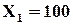 ;
; 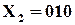 ;
; 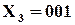 .
.
Похідгні: 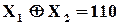 ;
; 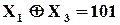 ;
; 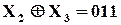 ;
; 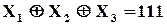
Повна сукупність:000,100, 010, 001, 110, 101, 011, 111.
Можна сказати, що базис “породжує” повну сукупність елементів групи плюс нульовий елемент, який повинен бути в групі за визначенням. Базис – компакт групи.
Наведений приклад ілюструє лише саму ідею представлення групи своїм базисом. Звичайно, щоб задати всі 3-розрядні комбінації, зовсім не потрібно вводити нові спеціальні поняття.
Візьмемо інший приклад:
100110 100110
 010011 010011
010011 010011
001101 001101
110101
Базис 101011
011110
111000
000000
Повна сукупність
(Звернемо увагу: ми задали 8 слів за допомогою трьох).
Базис зручно (у цьому переконаємося у подальшому) представляти відповідною матрицею. У нашому випадку
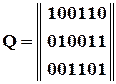 (2.9)
(2.9)
Таку матрицю називають породжуючою і майже завжди позначають символом 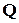 .
.
У більшості випадків процедура кодування полягає у доповненні вихідного (исходного – рос.) слова деякою кількістю додаткових (надлишкових або перевірочних) символів (розрядів). Будемо (як ми вже домовились) позначати кількість вихідних розрядів через 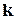 , а кількість додаткових – через (
, а кількість додаткових – через ( 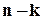 ), тобто
), тобто

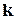 розрядів
розрядів  розрядів
розрядів
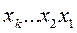
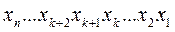
Зауважимо, що значення перших 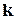 розрядів кодування повинні зберігатися. Це так звані систематичні (розділимі) коди.
розрядів кодування повинні зберігатися. Це так звані систематичні (розділимі) коди.
А з цього безпосередньо витікає, що в породжуючій матриці 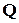 перші
перші 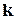 стовпців повинні утворювати одиничну квадратну матрицю рангу
стовпців повинні утворювати одиничну квадратну матрицю рангу 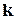 . Тільки у цьому випадку перші
. Тільки у цьому випадку перші 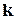 розрядів кодової комбінації зможуть приймати довільні значення. Виконання цієї вимоги є необхідним для того, щоб не накладати будь-яких обмежень на інформацію, що підлягає кодуванню. Таким чином,
розрядів кодової комбінації зможуть приймати довільні значення. Виконання цієї вимоги є необхідним для того, щоб не накладати будь-яких обмежень на інформацію, що підлягає кодуванню. Таким чином,
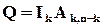 , (2.10)
, (2.10)
де 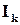 - одинична квадратна матриця рангу
- одинична квадратна матриця рангу 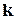 ;
; 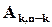 - матриця розмірності
- матриця розмірності 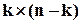 .
.
Нагадаю, що 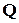 задає множину кодових слів, а кожен рядок
задає множину кодових слів, а кожен рядок 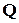 – це теж кодове слово. Тому всі вимоги до множини кодових слів повинні виконуватися і для рядків
– це теж кодове слово. Тому всі вимоги до множини кодових слів повинні виконуватися і для рядків 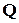 . Зокрема, якщо кодові слова повинні бути рознесені на відстань
. Зокрема, якщо кодові слова повинні бути рознесені на відстань 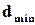 одне від одного, то ця ж сама вимога повинна виконуватись і для рядків
одне від одного, то ця ж сама вимога повинна виконуватись і для рядків 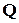 . Для нашого прикладу можна переконатися, що як для
. Для нашого прикладу можна переконатися, що як для 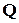 , так і для повної множини кодових слів, породжених
, так і для повної множини кодових слів, породжених 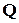 ,
, 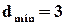 . (Згадаємо, що такий код спроможний корегувати всі однократні помилки). Тобто, виконавши певні вимоги до
. (Згадаємо, що такий код спроможний корегувати всі однократні помилки). Тобто, виконавши певні вимоги до 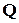 , ми забезпечуємо задані властивості для усієї множини кодових слів.
, ми забезпечуємо задані властивості для усієї множини кодових слів.
З точки зору математики процедура кодування еквівалентна матричному множенню довільного 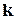 - розрядного слова
- розрядного слова 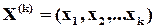 на породжуючи матрицю
на породжуючи матрицю 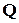 . Результатом такого множення буде добуток у вигляді
. Результатом такого множення буде добуток у вигляді  -розрядного слова
-розрядного слова 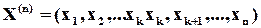 . Причому,
. Причому, 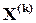 та
та 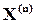 треба розглядати як вектор-рядки, а операції множення і додавання виконуються за правилами алгебри логіки:
треба розглядати як вектор-рядки, а операції множення і додавання виконуються за правилами алгебри логіки:
Проаналізуємо, що відбудеться при такому множенні:
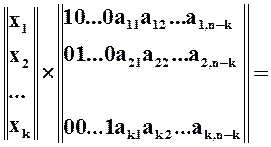

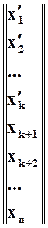
нагадаю, що 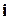 -й розряд добутку – це скалярний добуток
-й розряд добутку – це скалярний добуток 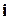 - го розряду
- го розряду 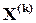 та
та 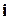 -го стовпця
-го стовпця 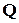 . Тобто
. Тобто
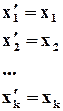

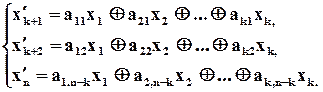
Останні 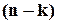 рівнянь називаються рівняннями кодування. Вони, по суті, в явній формі визначають залежність значень додаткових розрядів від значень інформаційних.
рівнянь називаються рівняннями кодування. Вони, по суті, в явній формі визначають залежність значень додаткових розрядів від значень інформаційних.
В узагальненому вигляді кожне рівняння кодування можна записати як
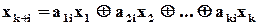 ,
, 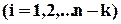 .
.
Це рівняння можна переписати так:
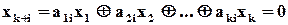 ,
, 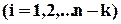 (2.11)
(2.11)
Треба підкреслити, що ми лише переписали рівняння, врахувавши особливості функції 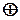 . Зокрема, ми маємо право переносити будь-який доданок з лівої частини в праву і навпаки без зміни знаку, бо від’ємні доданки не мають змісту.
. Зокрема, ми маємо право переносити будь-який доданок з лівої частини в праву і навпаки без зміни знаку, бо від’ємні доданки не мають змісту.
До цього моменту ми ніяк не враховували помилки, і рівняння (2.11) виконується, коли помилок немає. А якщо вони виникнуть, то може вже і не виконуватися, тобто
|
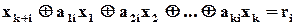 ,
, 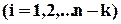 (2.12)
(2.12)
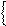 де
де 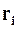 = 0, якщо помилки немає або вона не виявляється, та ri =1, коли помилка є.
= 0, якщо помилки немає або вона не виявляється, та ri =1, коли помилка є.
Рівняння (2.12) називаються рівняннями перевірки, а 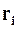 - результатом
- результатом 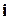 -ї перевірки.
-ї перевірки.
Сукупність 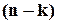 результатів перевірки називається перевірочною послідовністю або синдромом
результатів перевірки називається перевірочною послідовністю або синдромом
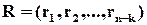 .
.
З точки зору математики обчислення синдрому може бути записане як результат матричного множення  -розрядного слова на деяку матрицю
-розрядного слова на деяку матрицю 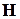 , яку називають перевірочною. Спосіб її утворення можна записати так:
, яку називають перевірочною. Спосіб її утворення можна записати так:
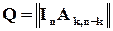 ;
; 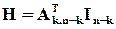 ,
,
де 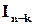 – одинична квадратна матриця рангу
– одинична квадратна матриця рангу 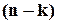 ,
, 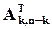 – транспонована матриця
– транспонована матриця 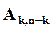 , тобто матриця, отримана із
, тобто матриця, отримана із 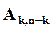 заміною рядків на стовпці:
заміною рядків на стовпці:

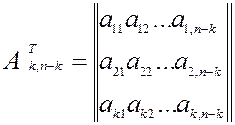 ;
; 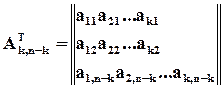 Таким чином, перевірочна матриця
Таким чином, перевірочна матриця 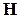 має
має 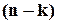 рядків і
рядків і  стовпців, а кожен рядок відповідає одній перевірці. З цього витікає, що результатом множення
стовпців, а кожен рядок відповідає одній перевірці. З цього витікає, що результатом множення  -розрядного слова на
-розрядного слова на 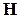 є саме синдром, тобто
є саме синдром, тобто
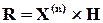
А тепер повернемось до власне помилок. А саме, яка відповідність між помилками та синдромами. Кодову комбінацію, яка спотворена помилкою, можна записати так:
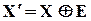 ,
,
де 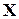 - комбінація без помилок, тобто та, яку передавало джерело інформації. Синдром, що відповідає
- комбінація без помилок, тобто та, яку передавало джерело інформації. Синдром, що відповідає 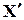
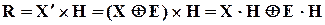
Але за визначенням 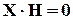 та
та
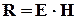 , (2.13)
, (2.13)
тобто синдром для певної конкретної помилки 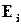 можна отримати, помноживши вектор помилки
можна отримати, помноживши вектор помилки 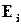 на перевірочну матрицю.
на перевірочну матрицю.
Ми вже знаємо, що в більшості випадків можна вважати, що найбільш ймовірними є однократні помилки. Тому, насамперед потрібно з’ясувати, який вигляд має відповідність між векторами однократних помилок і синдромами. Знайдемо синдроми, як відповідають однократним помилкам в  -розрядному кодовому слові.
-розрядному кодовому слові.
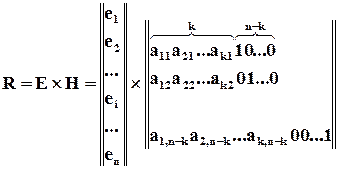
Оскільки 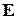 – вектор однократної помилки, то серед його компонент є тільки одна одиниця. З цього витікає, що синдром помилки в
– вектор однократної помилки, то серед його компонент є тільки одна одиниця. З цього витікає, що синдром помилки в 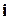 -му розряді кодового слова в точності співпадає з
-му розряді кодового слова в точності співпадає з 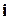 -м стовпцем матриці
-м стовпцем матриці 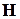 . Іншими словами, стовпці матриці
. Іншими словами, стовпці матриці  – це синдроми однократних помилок. Тому
– це синдроми однократних помилок. Тому
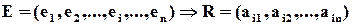 ,
,
де лише 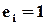 .
.
Тепер вже можна сформувати вимоги до перевірочної матриці групового коду для виявлення і виправлення помилок.
Виявлення помилок.
1. Помилка 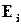 виявляється кодом, якщо
виявляється кодом, якщо 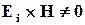 .
.
2. Перевірочна матриця коду, що виявляє всі однократні помилки, повинна мати  ненульових стовпців.
ненульових стовпців.
У найпростішому випадку
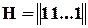 , і, відповідно,
, і, відповідно, 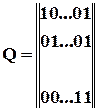
– це код з однією перевіркою на парність, що має один додатковий символ
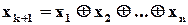 .
.
Рівняння перевірки
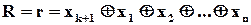 .
.








