Розділ 2. Методи контролю цифрових пристроїв
2.1. АПАРАТНІ МЕТОДИ ФУНКЦІОНАЛЬНОГО КОНТРОЛЮ
У відповідності з прийнятою термінологією всі методи контролю цифрових пристроїв поділяються на два класи: методи функціонального та тестового контролю. При функціональному контролі визначення технічного стану об’єкта (працездатний/непрацездатний) здійснюється безпосередньо у робочому режимі об’єкта без його “зупинки” для проведення процедур контролю, тобто є можливість подавати на входи пристрою лише робочі сигнали, які передбачені алгоритмом функціонування пристрою. При тестовому підході для контролю передбачається спеціальний тестовий режим, коли об’єкт не використовується за призначенням і на його входи подають спеціально підібрані тестові сигнали і впливи.
На рис. 2.1. показана узагальнена схема функціонального контролю, де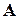 
- контрольований пристрій; 
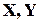- відповідно, вхідні і вихідні сигнали пристрою, 
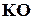– деякий контрольний орган, вихідний сигнал якого 
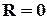, коли 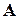функціонує правильно і 
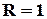, коли в 
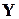з’являються помилки. 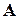разом із 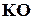іноді називають схемою із самоконтролем.
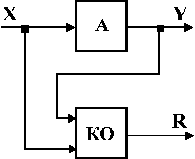
Рис. 2.1.
При застосуванні функціонального контролю виникають дві основні задачі: забезпечити максимальну повноту контролю, тобто по можливості виявляти більшість помилок, які можуть мати місце при функціонуванні 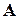; і знайти такі реалізації 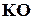, які дозволяють мінімізувати апаратні витрати при здійсненні контролю.
Очевидним способом функціонального контролю є схема на рис. 2.2, в якій функції 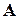фактично повторюються дублікатом 
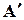і після цього вихідні сигнали порівнюються для утворення сигналу помилки 
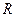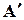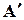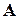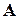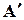. Така схема вимагає подвоїння апаратних витрат, але в то же час дозволяє виявляти всі помилки в контрольованому пристрої за винятком таких, які можуть одночасно виникнути в . Не виявляються тільки такі помилки, які виникають в в тих же самих розрядах, що і в , і одночасно з ними. Як ми вже з’ясували раніше, ймовірність такої події при незалежній реалізації і дуже мала.
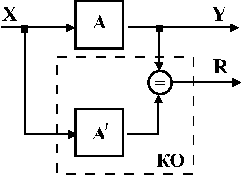
Рис. 2.2.
Дублювання контрольованого пристрою із наступним порівнянням виходів є, так би мовити, примітивним розв’язком задачі функціонального контролю, оскільки вимагає подвоїння апаратних витрат. Не зважаючи на цю ваду, така схема застосовується і на практиці завдяки високій ефективності з точки зору повноти контролю.
Пошук більш економних схем функціонального контролю може йти, в основному, за рахунок зменшення його повноти. Так, коли немає необхідності виявляти всі можливі помилки, замість повного дублікату 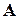у складі можна використати його спрощену копію. Наприклад, для контролю арифметичних операцій досить часто застосовують так званий “контроль” по модулю”. (рис. 2.3).
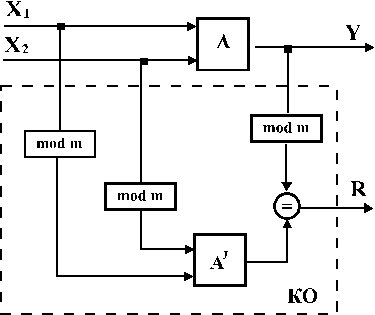
Рис. 2.3.
У цьому випадку у 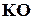попередньо обчислюють остачі від ділення кожного із операндів 
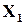та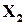 
на деякий модуль 
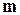, після цього над отриманими остачами виконують ту ж саму операцію, яку виконує пристрій 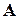. Результат контрольованого пристрою 
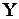теж згортається по модулю m, після чого результати обчислення в 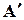й отримана згортка порівнюються для утворення сигналу помилки.
Враховуючи, що 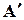працює із суттєво меншою кількістю розрядів, складність 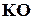загалом може бути теж зменшена. Зрозуміло, що якщо, наприклад, 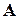виконує операції із 16- або 32-розрядними двійковими словами, то при 
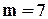після згортки розрядність 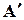зменшується до 
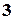, а при 
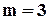– до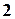 
. Зрозуміло також, що контроль по модулю має застосування, обмежене, головним чином, арифметичними пристроями.
Однак сама по собі ідея виконувати в 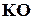деяку спрощену функцію по відношенню до функції пристрою 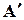безумовно, заслуговує на увагу. У багатьох випадках нам важливо уникнути тільки грубих помилок, які можуть вплинути на безпеку об’єкта управління, а помилки, які не впливають на безпеку (наприклад, такі, що пов’язані із похибками давачів) можна ігнорувати. Із цією метою при реалізації 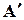можна використовувати усічений алгоритм, за яким обчислюється значення тієї ж самої функції, що і 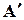, але тільки над обмеженою кількістю старших розрядів, ігноруючи значення молодших розрядів. Природно, що при цьому складність 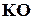зменшується. Але ж не будемо забувати, що і повнота контролю при цьому теж зменшується, тобто відбувається обмін повноти на складність. Саме із цієї причини необхідно провадити ретельний аналіз помилок (а вони є наслідком несправностей контрольованого пристрою) з точки зору їх впливу на кінцевий результат обчислень.
З другого боку, не слід нехтувати помилками, які принципово не можуть бути виявлені. Про них вже йшла мова – це однотипові помилки, які одночасно можуть виникнути в 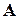і 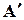. Щоб зменшити ймовірність саме таких помилок, бажано не тільки застосовувати незалежну реалізацію 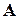і 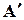, але й по можливості реалізувати їх по-різному (вони не повинні бути однаковими). Один із таких способів полягає у наступному.
Дублюючий пристрій 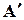реалізує не ту саму функцію 
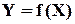, що 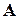, а її інверсію, тобто для 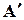.(рис. 2.4)
.
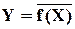У цьому випадку, природно, 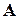і 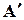будуть різними, ймовірність однотипових помилок зменшується. Такий метод отримав назву “двопровідної логіки”. На рис. 2.5. наведений приклад застосування методу для простої комбінаційної схеми, що реалізує функцію
,
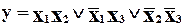тоді 
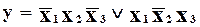
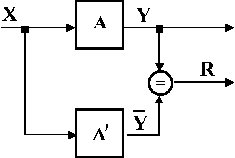
Рис. 2.4.
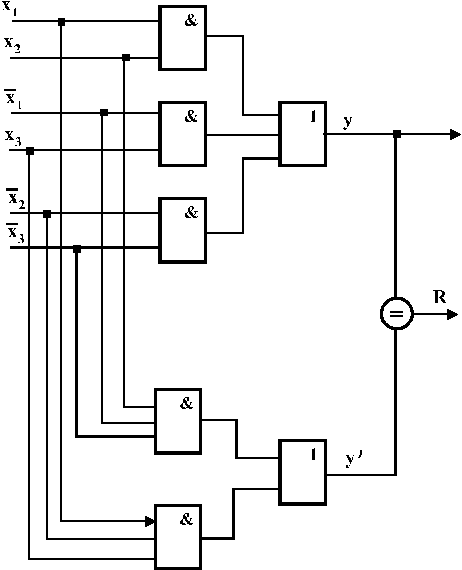
Рис. 2.5.
Зміст сигналу помилки теж дещо змінюється. Зокрема, 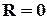, коли помилка є, і 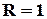, коли немає.
У деяких випадках може виявитися ефективним метод “зворотної машини” (рис. 2.6.), який передбачає реалізацію зворотної функції
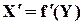
і порівняння обчисленого значення вхідного сигналу із реальним значенням.
Рис. 2.6.
Необхідною умовою можливості застосування цього методу є існування зворотного перетворення, тобто принципова можливість обчислення вхідних даних на основі вихідних. На жаль, така можливість існує лише для небагатьох перетворень. Так, вже навіть для арифметичних функцій не існує зворотних перетворень (знаючи тільки суму, неможливо знайти доданки, за добутком – множники і т.д.). Але для деяких функцій така можливість існує, наприклад для піднесення у степінь зворотним є обчислення кореня. Для більшості тригонометричних функцій також легко знайти зворотні перетворення.
Класичним прикладом застосування методу “зворотної машини” є функціональний контроль аналого-цифрового перетворення (АЦП), зворотним до якого є цифро-аналоговий перетворювач (ЦАП) (рис. 2.7.). Оскільки ЦАП за складністю суттєво простіший за АЦП, такий контроль виявляється досить економним за апаратними витратами і, в той же час, виявляє практично всі можливі помилки АЦП.
Метод “зворотної машини” є досить універсальним, зокрема його можна реалізувати і програмно, звичайно, лише в тих випадках, коли зворотне перетворення існує, тобто тоді, коли за результатом обчислень можливо розрахувати вихідні дані і переконатись, що вони співпадають з тими, які були використані при обчисленнях.
Як бачимо, арсенал існуючих методів функціонального контролю досить великий, що дозволяє в широких межах змінювати як апаратні витрати, так і повноту контролю, яка визначає його ефективність.
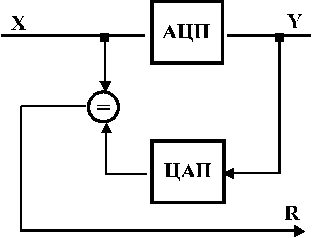
Рис. 2.7.
У загальному випадку пошук оптимальних схемних рішень базується на ідеї селективності контролю, тобто на обмеженні сукупності помилок тільки такими, які найбільш ймовірні і одночасно найбільш небезпечні з точки зору впливу на об’єкт управління.
Виникає питання: чим визначається ймовірність появи тієї чи іншої помилки? Що є первинним у визначенні таких ймовірностей? Очевидно, потрібно шукати, так би мовити, в “матеріальній” сфері, тобто в тих фізичних процесах, які відбуваються в компонентах пристрою і призводять до втрати працездатності. Із цієї точки зору первинними є несправності компонентів, а їх проявом є помилки на виходах пристрою. Враховуючи розгалужену топологію сучасних електронних пристроїв, одиночні помилки здебільшого призводять до багатократних помилок на виходах схеми, причому ці помилки специфічні у тому розумінні, що проявляються вони не на всіх вхідних сигналах. Зрозуміло, щоб виявити цю специфічність і сформувати вимоги до засобів контролю, необхідно провести ретельний аналіз топології внутрішніх зв’язків контрольованого пристрою з точки зору розповсюдження спотворених сигналів і на цій основі отримати множину найбільш ймовірних помилок.
Наступним кроком в оптимізації апаратних витрат на контроль є побудова такого 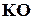, який би виявляв всі помилки із сформованої множини.
Для того щоб перейти до відповідних методів синтезу 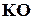нам не обійтись без розгляду хоча б загальних основ теорії завадостійкого кодування. Слід додати також, що і деякі методи діагностування несправностей також базуються на використанні саме таких кодів
Контрольні питання
1. У чому полягає різниця між функціональним та тестовим контролем?
2. Що є визначальним при виборі методу функціонального контролю?
3. Що таке “двопровідна логіка”?
4. У чому полягає метод “зворотної помилки”? У яких випадках цей метод не може бути застосованим?
5. Із яких міркувань формується множина помилок, які необхідно виявляти при функціональному контролі?
2.2. ЗАВАДОЗАХИЩЕНЕ КОДУВАННЯ
Фундаментальним поняттям в захисті від завад є інформаційна надлишковість. За К. Шеноном інформаційна надлишковість оцінюється як
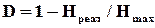, (2.1)
де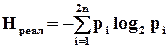 
; (2.2)
– розрядність слів при двійковому кодуванні.
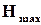– максимальна ентропія, яка має місце, коли всі 
( 
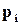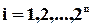) однакові, тобто 
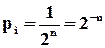і ентропія може бути визначена за формулою Хартлі
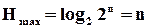(2.3)
При будь якому відхиленні від рівномірного розподілу можна говорити про інформаційну надлишковість, і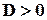 
.
До речі, інформаційну надлишковість іноді зручніше вимірювати просто як
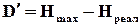(2.4)
Нас буде цікавити випадок, коли деяка частина -розрядних слів із загальної кількості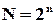 
не використовується. Позначимо кількість таких слів через 
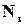і будемо називати їх забороненими. Це означає, що деякі ймовірност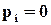і 
і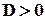 
. Підмножина слів, кількість яких 
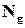, є дозволеними словами і використовуються джерелом інформації для кодування повідомлень.
Очевидно,
.
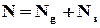