3.Який алгоритм відновлення сигналів при застосуванні мажоритарного методу?

Дата: 2025-05-21; Просмотры: 5
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

4.Як впливає поріг прийняття рішень при відновленні сигналів на надійність і достовірність?

1.5. ІНФОРМАЦІЙНА НАДЛИШКОВІСТЬ ЯК УНІВЕРСАЛЬНИЙ ЗАСІБ КОНТРОЛЮ

Традиційно поняття інформаційної надлишковості (ІН) найчастіше пов’язують із використанням завадозахищених кодів для передачі і зберігання інформації. За К. Шенноном рівень ІН визначається відносним перевищенням максимально можливої ентропії 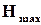над реальною ентропією 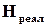конкретного джерела інформації при використанні певного способу кодування

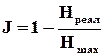, (1.18)

або в абсолютному обчисленні

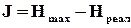, (1.19)

де 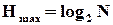та ,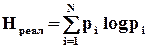

а 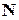– кількість можливих повідомлень, 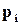- ймовірність використання (появи) 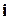-го повідомлення.

Таке перевищення виникає при будь-якому відхиленні розподілу ймовірностей появи окремих повідомлень від рівномірного (при кодуванні повідомлень комбінаціями символів однакової довжини). В частинному випадку, коли окремі комбінації джерелом не використовуються (ймовірність їх появи дорівнює 0), множина всіх можливих повідомлень 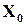природно розпадається на дві підмножини: підмножину дозволених слів 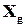(слів, які використовуються джерелом), та підмножину заборонених слів 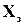(слів, які джерелом не використовуються). Цей випадок із практичної точки зору є найбільш цікавим, про що піде мова нижче.

Якщо підходити до ІН менш формально, то її присутність проявляється у специфічності, точніше, індивідуальності джерела. При використанні завадозахищених кодів ця індивідуальність досягається додаванням перевірочних сигналів, утворених за певними правилами. Виконання саме цих правил і робить джерело індивідуальним, тобто таким, яке можна впізнати і відрізнити від інших, якщо ті використовують інші способи кодування. Перевірка виконання штучно введених правил дозволяє виявляти та (або) виправляти помилки, які виникли при передачі чи зберіганні інформації.

Але наявність ІН не є обов’язковою для того, щоб джерело було індивідуальним. Адже навіть у випадку, коли всі повідомлення рівноімовірні ( 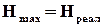та 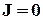), джерело залишається специфічним. Його індивідуальність саме в тому і полягає, що всі повідомлення рівноімовірні, а відхилення від рівноімовірності може свідчити про наявність помилок при передачі або збереженні інформації. Цю ситуацію можна вважати навіть парадоксальною: жодної надлишковості немає, а помилки, принаймні деякі, можна виявити.

Таким чином, можна вважати, що будь-яке джерело з відомою та стаціонарною статистикою повідомлень ( навіть джерело білого шуму) є специфічним. А якщо цю специфіку можна визначити за допомогою деяких формальних правил, то можна й виявити помилки. Із цього витікає, як наслідок, що контроль достовірності будь-якого джерела можна здійснити без введення штучної надлишковості . Таке ствердження не є результатом формального доведення. Це, скоріше, припущення, на користь якого можна навести безліч прикладів. Саме це ми й зробимо у подальшому.

1. Повідомлення генеруються джерелом із різною ймовірністю, розподіл довільний, заданий спектрограмою, отриманою, наприклад, як результат тривалого спостереження за повідомленнями джерела. Така спектрограма зображує відносні частоти появи того чи іншого слова (символу). Відомо, наприклад, що в англійській мові символ (літера) 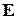з’являється із відносною частотою (ймовірністю) 0,12, символ 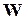- 0,02 і т.д. В українській – розподіл інший. Найбільшу частоту мають літери 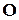(0,08) та 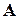(0,07), а найменшу - 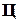(0,0044) та 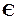(0,0037).

Саме розподіл частот характеризує індивідуальність відповідного джерела. Це – як відбитки пальців людини, за якими її можна “впізнати”, тобто ідентифікувати.

З точки зору контролю частотний розподіл можна вважати досить надійним критерієм достовірності інформації. Будь-яке суттєве відхилення розподілу від зафіксованого за тривалий час спостереження є ознакою виникнення помилок. Ясно, що поодинокі відхилення (одиночні помилки) навряд чи призведуть до порушення розподілу і тому не можуть бути надійно виявлені. Це, зрозуміло, є принциповою вадою всіх без винятку статистичних методів контролю. Більш того, навіть у випадках, коли помилки мають регулярний характер, їх можна виявити тільки із запізненням, знову ж таки за тривалий час спостереження. Із цього витікає, що безпосередньо статистичний метод контролю не може бути оперативним, і тому він непридатний для контролю у випадках, коли отримана від джерела інформація зразу ж використовується для управління реальними об’єктами, коли помилки, навіть одиночні, можуть виявитися неприпустимими з точки зору можливих наслідків і втрат.

2. У частотному розподілі є “провали” – деякі повідомлення (слова або символи) мають нульову ймовірність при нормальному функціюванні об’єкта контролю (джерела). Вони утворюють підмножину заборонених слів 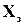. Поява будь-якого слова із 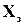є ознакою помилки, яка може бути виявлена практично миттєво апаратними чи програмними засобами. Для цього достатньо знати склад 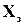. Враховуючи, що підмножина дозволених слів 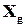та 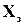взаємно доповнюють одна одну до множини всіх можливих слів 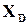, тобто

,

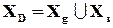можна обмежитись фіксацією лише однієї підмножини. Звичайно, для такої фіксації та реалізації відповідних процедур контролю необхідні вільні обчислювальні ресурси, насамперед, пам’ять. Але головна проблема не в ресурсах, а в часових обмеженнях, адже процедуру контролю необхідно виконувати кожного разу при надходженні чергової порції повідомлень, а для цього необхідний час. Тому процедури контролю мають бути максимально короткими за часом і простими. На цій проблемі ми зупинимось трохи далі, а зараз звернемо увагу на таке.

З теоретичної точки зору між ситуаціями 1 і 2 немає принципової різниці. І в першому, і в другому випадку властивості джерела описуються однаково – довільним частотним розподілом, і цей розподіл можна використати як еталон для виявлення помилок. Але з точки зору практичної реалізації та ефективності контролю за критерієм мінімуму часу, за який помилка може бути виявлена, друга ситуація принципово відрізняється від першої. Саме наявність слів із нульовою ймовірністю дає можливість виявляти відповідні помилки практично в момент їх появи. Виникає питання: а що робити в ситуації 1? Чи можна дати собі раду у цьому випадку? Виявляється, що так. Вихід може підказати все таж класична робота К. Шенона. Цей вихід дуже простий і прозорий. Якщо розглядати частотний розподіл, утворений парами слів, які надходять від джерела у сусідні моменти часу, то майже напевне виявляється, що деякі пари мають нульову ймовірність надходження. Це свідчить, що ми автоматично переходимо до ситуації 2 і отримуємо можливість оперативного виявлення помилок. Якщо ж ми перейдемо до розподілу “”трійок”, “четвірок” і т.д. сусідніх за часом повідомлень, то кількість таких штучно об’єднаних слів, що мають нульову ймовірність, буде зростати у геометричній прогресії.

Для ілюстрації можна навести приклад повідомлень, що надаються, наприклад, українською мовою. На рівні окремих літер у частотному розподілі немає провалів – у текстах використовуються всі літери, але з різною ймовірністю. Але вже в розподілі пар такі провали з’являються: м’який знак не може використовуватися після голосних та на початку слова, не використовуються літеросполучення “дє”, “кє” та інші сполучення літери “є” з приголосними та голосними.

Це були, так би мовити, лінгвістичні приклади, які начебто не мають відношення до контролю електронних приладів та комп’ютерних систем. Але ж, якщо уважно проаналізувати, наприклад, повідомлення від конкретного давача в комп’ютерну систему управління технологічним об’єктом, то можна зауважити певні закономірності, що мають місце у статистичній структурі таких послідовностей. Наприклад, якщо це значення температури рідини, яку нагрівають, то ці значення будуть зростати, і кожне значення температури в момент часу 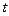буде не менше, ніж в момент часу 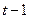. Або, наприклад, тиск у об’ємі, що зменшується, не може теж зменшуватися, бо відповідно до закону Бойля-Маріота добуток тиску на об’єм повинен залишатися постійним, 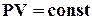. До речі, саме ця залежність може бути використана у відповідних випадках як надійна контрольна ознака достовірності даних, що надходять від об’єкта в систему управління. У багатьох інших випадках саме “зв’язаність” деяких параметрів фізичними законами може виявитися найбільш корисною для організації ефективного контролю.

Ще один приклад. В типових комп’ютерних системах промислового призначення більша частина інформації надходить до системи шляхом регулярного опитування здавачів за певним (фіксованим) часовим регламентом. Як наслідок, повідомлення від окремих давачів, що характеризують параметри одного технологічного процесу, обов’язково будуть корельовані тому, що це параметри одного і того ж процесу, який не може виходити за межі відповідних фізичних (хімічних) законів. Тому, як і в попередньому випадку, виконання цих законів може бути ефективно використано для перевірки достовірності даних. Зауважимо, що саме корельованість даних свідчить, про наявність 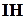, тому в таких випадках введення штучної 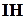не є обов’язковим. І головне, контроль на основі 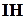, яку логічно назвати природною, охоплює не тільки помилки засобів передачі даних (як це має місце при застосуванні штучної 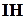), а й увесь автоматизований комплекс, тобто порушення технологічного процесу та несправності засобів автоматизації. А це найбільш суттєво з точки зору загальної ефективності контролю та запобігання аварійних ситуацій.

Повернемось тепер до більш конкретних задач, пов’язаних з реалізацією контролю на основі природної 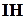. Можна сподіватись, що наведені розміркування і приклади досить переконливо свідчать на користь існування майже у всіх цікавих з практичної точки зору випадках природної ІН. Таким чином, залишається основне питання: як цю надлишковість використати для організації контролю працездатності або технічного стану об’єкта. Для цього необхідно розв’язати, принаймні дві задачі.

По-перше, бажано попередньо оцінити ефективність контролю щодо його повноти, тобто визначити, наприклад, яку частину всіх можливих помилок можна принципово виявити при його застосуванні. По-друге, потрібно побудувати основні процедури, що дозволяють реалізувати контроль у складі існуючих або таких, що проектуються, комп’ютерних систем.

Перша задача може бути розв’язана на основі досить простих міркувань. Розглянемо випадок, коли джерело (давач, первинний перетворювач, клавіатура, з якої оператор вводить виробничу інформацію в систему, тощо) формує повідомлення у вигляді двійкових слів фіксованої розрядності . Тоді загальна кількість всіх можливих помилок (векторів помилок) може бути записана як ( ).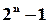

Вектор помилки – це двійкова -розрядна комбінація, в якій 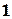відповідають тим розрядам, що створені помилками. Наприклад, якщо правильна комбінація

,

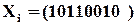а після спотворення помилкоюотримали

,

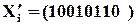то відповідний вектор помилки

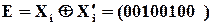
де 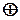- порозрядна сума по модулю 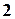. Для наочності цю операцію можна записати так

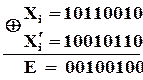
З іншого боку, очевидно, можуть бути виявлені тільки такі помилки, які переводять (перетворюють) дозволене слово в заборонене. Тому кількість помилок, що можуть бути виявлені, у точності дорівнює кількості заборонених слів (позначимо цю кількість через 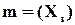). Тоді частина помилок, які можна виявити

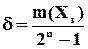, (1.20)

Висновок із цього важливого співвідношення очевидний: чим менше слів (комбінацій із числа, всіх можливих використовується, тим більше помилок можна виявити. Але цей висновок занадто загальний, щоб ним скористатися конструктивно, тобто для того, щоб визначити конкретні помилки, які можна виявити, та побудувати відповідні процедури корекції.

Тут необхідно зазначити, у загальному випадку, очевидно, не всі можливі помилки реально можуть виникнути, і крім того, з тих помилок, які можуть реально виникнути, не всі однаково небезпечні. Тому має сенс диференціювати елементи підмножини 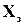у відповідності з двома видами помилок: помилки, які обов’язково повинні бути виявлені, і помилки, які корегувати не обов’язково. Мова йде, фактично, про скорочення кількості помилок, які підлягають виявленню, враховуючи тільки такі помилки, які найбільш ймовірні або найбільш небезпечні з точки зору функціонування об’єкту управління. Таке скорочення дозволяє спростити відповідні процедури контролю, що дуже важливо при їх апаратній реалізації.

В деяких випадках рівень 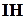такий, що дозволяє не тільки виявляти, але й виправляти помилки. Розглянемо, за яких умов це можливо. Для наочності скористаємося графічним представленням помилок у вигляді переходів між повідомленнями, або, точніше, перетворень дозволених слів у заборонені (рис. 1.12).

 

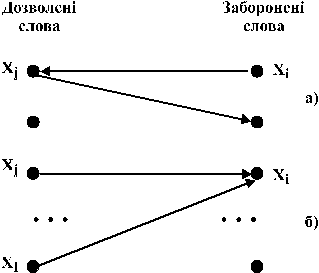
Рис. 1.12.

Очевидно, необхідною умовою можливості виправлення конкретної помилки є однозначність зворотного переходу від слова 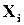, яке містить помилку, до слова без помилок 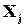. Очевидно, що така однозначність має місце лише у випадку, коли в кожне заборонене слово переходить не більше одного дозволеного слова (ситуація а). Коли ж в одне заборонене слово переходить кілька дозволених (ситуація б), визначити “зворотний шлях” для виправлення помилки практично неможливо, не маючи підстав для того, щоб віддати перевагу одному із варіантів зворотного переходу. Виходячи із таких простих розміркувань, можна стверджувати, що для виправлення 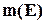помилок у кожному дозволеному слові повинно існувати 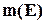відповідних заборонених слів. Для всіх дозволених слів джерела можна записати

,

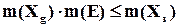звідки 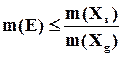. (1.21)

Отримане співвідношення визначає рівень 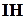, необхідний для виправлення 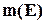векторів помилок при довільному способі кодування, і може слугувати критерієм для попередньої оцінки потенційної корегуючої здатності того чи іншого способу представлення інформації відповідним джерелом. Як ми побачимо далі, ця формула має універсальний характер і може бути застосована і у випадку штучної 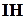, наприклад, при використанні заводостійких кодів.

Контрольні питання

1.У чому проявляється наявність інформаційної надлишковості.

2.Що таке “природна” інформаційна надлишковість? Наведіть приклади її присутності.

3.Чим визначається здатність до виявлення або або виправлення помилок?

4.Яким чином можна штучно збільшити рівень інформаційної надлишковості?