2. Які шляхи підвищення надійності для об’єктів цих класів?
3. Що таке структурна надлишковість?
4. Як впливає складність об’єкту на його надійність?
5. Що таке коефіцієнт готовності і як можна його підвищити?
1.4. Резервування апаратури
Резервуванням називається метод підвищення надійності шляхом включення резервних елементів при розробці системи або в процесі її експлуатації.
Розрізняють загальне та поелементне резервування. За способом включення резерву – постійне і заміщенням. У випадку резервування заміщенням резерв може бути ненавантаженим, полегшеним і навантаженим.
Зрозуміло, що резервування ускладнює апаратуру і може бути реалізовано не для усіх видів електронного обладнання та його рівнів. Наприклад, поелементне постійне резервування на рівні окремих радіоелементів (резисторів, конденсаторів, транзисторів, тощо) не може бути здійснено через неможливість забезпечити незмінність параметрів резервованої схеми у процесі виникнення несправностей. Хоча теоретично поелементне резервування є найбільш доцільним з точки зору апаратних витрат, на практиці його можна застосувати головним чином на рівні функціонально закінчених блоків (винятком є чисто цифрова апаратура, де поелементне постійне резервування може бути реалізоване на будь-якому рівні).
Загальне резервування (резервується весь пристрій в цілому) застосовується здебільшого у великих електронних системах, багатокомп’ютерних комплексах та мережах і вимагає досить складного програмного узгодження функцій кожного компонента при втраті працездатності.
З точки зору ефективності найбільш привабливим слід вважати резервування заміщенням (резервирование замещением – рос.). Ідея цього методу дуже проста: коли основний елемент структури виходить з ладу, замість нього включається резервний. Це і є заміщення. Переваги такого способу резервування полягають в тому, що:
- один резервний елемент може бути використаним для кількох основних;
- резервні елементи можуть знаходитись у пасивному стані (наприклад, бути знеструмлені), що зберігає їх технічний ресурс;
Розглянемо на прикладах, що це дає з точки зору підвищення надійності. Спочатку розрахуємо ймовірність безвідмовної роботи найпростішої структури (один основний елемент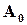 
і один резервний 
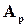(рис.1.6.).
Заміщення здійснює деякий перемикач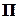 
(це може бути і оператор). Ймовірності безвідмовної роботи основного і резервного елементів – 
.
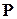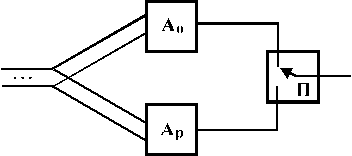
Рис.1.6
Структура буде залишатися працездатною в таких ситуаціях:
1) обидва елементи (основний і резервний) працездатні, ймовірність такої події –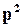 
;
2) основний елемент справний, резервний вийшов з ладу, відповідна ймовірність –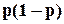 
;
3) навпаки, резервний елемент справний, основний відмовив, відповідна ймовірність –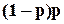 
.
Ймовірність безвідмовної роботи структури можна записати як суму
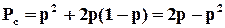
Враховуючи реальну надійність перемикача,
.
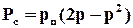Приймемо спочатку, що перемикач абсолютно надійний і ймовірність його безвідмовної роботи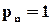 
. Для прикладу розрахуємо ефект в підвищенні надійності при наведеній схемі резервування. Нехай 
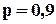, тоді маємо 
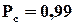, тобто ймовірність відмови зменшилась на порядок з 
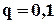до 
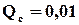. Але ж такий результат ми отримали, прийнявши ідеалізований випадок, коли 
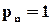. Насправді ж в реальних випадках такого не буває. Ясно, що при ненадійному перемикачеві ми можемо навіть зіпсувати справу, тобто погіршити надійність. Знайдемо, за яких умов цього не трапиться. Очевидно, якщо
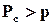або
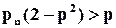і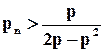 
, (1.11)
ми будемо мати підвищення надійності. Для нашого прикладу при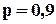
,
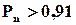тобто перемикач повинен мати, принаймні, надійність того ж порядку, що і основний та резервний елементи.
Розглянемо структуру, коли один резервний елемент використовується на два основних (рис. 1.7).
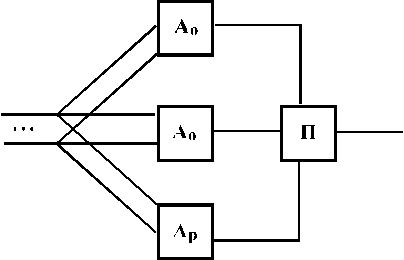
Рис.1.7
У цьому випадку структура, очевидно, буде залишатися працездатною, коли працездатними будуть перемикач і хоча б два з трьох елементів (двох основних і одного резервного). Для ймовірності безвідмовної роботи структури можна записати
.
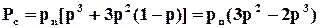При тій же надійності основних та резервного елементів і 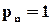отримаємо 
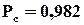. Як бачимо, у порівнянні із попереднім прикладом, ефект у підвищенні надійності трохи гірший. Це можна пояснити меншим рівнем надлишковості.
У загальному випадку резервування заміщенням, коли з 
елементів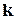 
є резервними, можна записати :
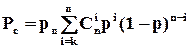. (1.12)
А тепер повернемось до “загадкового” перемикача. Реалізація функції переключення на резерв залежить від природи і функцій елементів, які потрібно переключати. Перемикачем може бути людина (оператор), коли операція переключення є складною. Наприклад, для того щоб переключитися на резервне живлення від дізель-генератора при зникненні напруги в мережі, потрібно виконати ряд досить складних операцій, які важко автоматизувати. Коли ж таким компонентом є та ж сама лампочка розжарення, неважко створити простий автомат, який при перегоранні однієї лампочки включить іншу. Загалом, створення відповідного автомату в багатьох випадках є проблемою головним чином через те, що потрібно мати чіткі і однозначні критерії працездатності (непрацездатності) відповідного компонента системи. Такі критерії не завжди легко знайти, особливо для багатофункціональних компонентів. Але у будь-якому випадку вимоги до надійності перемикача досить жорсткі, тому що саме цей показник обмежує надійність резервованої системи
Перейдемо тепер до розгляду класичного методу резервування, про який вже згадувалось раніше. Мова піде про метод Дж. Фон Неймана, який найчастіше називають мажоритарним. Це, по суті, постійне резервування із логічним переключенням на резервні елементи. У найпростішому випадку метод потребує мінімум потроїння апаратних витрат. Схема включення елементів структури показана на рис. 1.8.
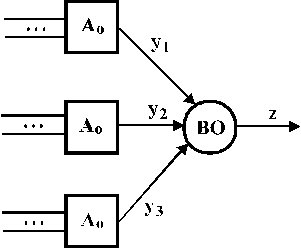
Рис. 1.8
На всі три елементи подаються однакові вхідні сигнали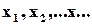 
Вихідні сигнали 
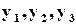надходять на так званий відновлюючий орган (ВО), функція якого полягає в утворенні результуючого сигналу за більшістю значень 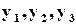(вхідні сигнали для ВО “голосують”). Для двійкових сигналів функцію ВО можна записати так
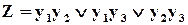
– це так звана мажоритарна функція алгебри логіки, звідси й одна із назв методу. По суті, значення сигналу, який відрізняється від інших, ігнорується. Обґрунтувати такий алгоритм прийняттям рішень можна таким чином.
Якщо позначити ймовірність відмови одного елемента через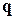 
, то ймовірність одночасної відмови зразу двох елементів (при незалежності цих подій) буде 
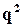. Очевидно, враховуючи, що 
,
,
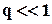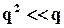тому є всі підстави вважати, що відмовив саме один елемент, а не два одночасно. Так, для сучасних елементів обчислювальної техніки ймовірність відмови за кілька годин роботи має порядок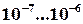 
, тоді 
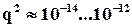, і можна впевнено прийняти рішення про відмову саме одного елемента, а не двох одночасно. Зазначимо ще раз, що такі розміркування чинні лише за умови незалежності відмов, тобто тільки в разі відсутності загальної першопричини відмов, наприклад, завад по колам живлення.
При більших рівнях надлишковості алгоритм прийняття рішень залишається таким самим – вихідний сигнал ВО визначається більшістю значень вхідних сигналів. Для ймовірності безвідмовної структури при -кратному резервуванні можна записати
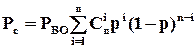, (1.13)
де, як і раніше,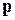 
- ймовірність безвідмовної роботи одного елемента структури; 
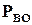- відповідна ймовірність ВО; 
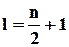для парних і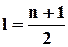 
для непарних. Зауважимо, що в (1.12) 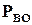входить як множник і тому обмежує значення 
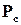, тобто 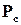завжди менше 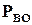. Це є принциповою вадою структури на рис.1.8 , яка має назву однолінійної.
Для того, щоб зняти це обмеження, застосовують багатолінійні структури (рис. 1.9), в яких ВО теж - кратно резервується. Для таких структур можна записати
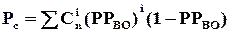. (1.14)
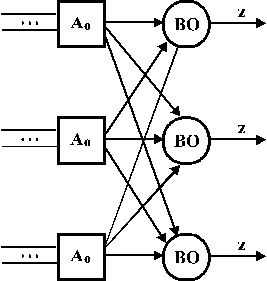
Рис.1.9.
Найважливішим для таких структур є зниження обмежень на надійність ВО та можливість досягнення будь-якої високої надійності структури при зростанні рівня надлишковості . Теоретично при деяких несуттєвих обмеженнях на початковий рівень надійності елементів 
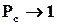при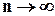 
(рис. 1.10). Це означає, що за рахунок надлишковості можна побудувати практично абсолютно надійні структури із компонентів, які мають обмежену надійність.
Окрім надлишковості для багатолінійних структур є характерним багатолінійні зв’язки між послідовними каскадами структури (Дж. Фон Нейман назвав їх “пучками зв’язків”), тобто всі сигнали в такій структурі розповсюджуються по багатьом каналам, що також сприяє підвищенню надійності. Однак з практичної точки зору виникає проблема “останнього ВО”, оскільки користувач повинен мати не сигналів, а один. З цього виходить, що на кінцевому виході необхідно буде об’єднати сигнали, і цей останній ВО буде обмежувати надійність цієї структури.
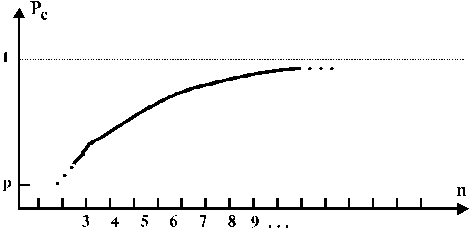
Рис. 1.10.
На користь ефективності багатолінійних мажоритарних структур свідчать також дослідження нейрофізіологів: є деякі підстави вважати, що саме за таким принципом побудована більшість біологічних систем, зокрема наш мозок. Ті ж дослідження показують, що надлишковість біологічних систем на клітинному рівні дуже висока (принаймні, мова йде про порядки).
Для технічних об’єктів навіть для сучасної мікроелектроніки такий рівень, звичайно, нереальний. На сьогодні у випадках, коли необхідно забезпечити високий рівень надійності найчастіше застосовують потроїння апаратури (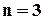 
), в деяких особливо відповідальних випадках застосування 
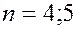, але більші рівні надлишковості є вже винятком.
Не звавжаючи на поширеність мажоритарного методу, слід мати на увазі, що при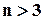 
цей метод не є оптимальним. Щоб довести це, розглянемо, наприклад, структуру з 
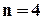. Така структура при відмові одного елемента залишається ще працездатною, але вже при двох несправних елементах перестає правильно функціювати (значення двох сигналів на входах ВО дорівнює 1 і двох – 0, більшості немає). В той же час в структурі ще залишається два повністю працездатних елемента, а сама структура вже непрацездатна (!). Із цієї точки зору принцип більшості не є найкращим.
Інший алгоритм, що позбавлений вказаного недоліку, полягає в наступному: елемент, вихідна реакція якого відрізняється від реакцій інших елементів, відключається і в подальшому не приймає участі в утворенні результуючого сигналу. Така своєрідна “ампутація” дозволяє зберегти працездатність структури аж до моменту, поки хоча б два елементи структури залишається працездатним. Може виникнути питання, чому саме два, а не один. Справа в тому, що в ситуації, коли залишилося останніх два елементи і виходить з ладу передостанній, неможливо впевнено віддати перевагу одному з них і тим самим утворити правильний результуючий сигнал
Зрозуміло, що реалізація такого алгоритму більш складна, ніж мажоритарного. Це вже має бути не комбінаційна схема, а автомат із пам’яттю, проте його реалізація сучасними засобами мікроелектроніки не викликає жодних проблем.
Тепер з’ясуємо, який ефект в підвищенні надійності можна отримати, застосовуючи ВО з пам’яттю. Ймовірність безвідмовної роботи, як і при мажоритарному ВО, очевидно зростає. Формули для обчислення цієї ймовірності співпадають з (1.12) для однолінійних і (1.13) – для багатолінійних структур. Відміна полягає лише в кількості доданків, які утворюють суму, - кількість їх зростає з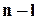 
до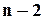 
, тобто для однолінійних структур з ВО з пам’яттю
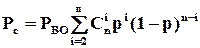(1.15)
та багатолінійних
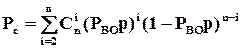(1.16)