3. В чому різниця між частотою та інтенсивністю відмов?
НАВЧАЛЬНИЙ ПОСІБНИК З КУРСУ
«КОНТРОЛЬ, ДІАГНОСТИКА та НАДІЙНІСТЬ
Т/К СИСТЕМ І МЕРЕЖ”
( УКЛАДАЧ – Ю.Г.САВЧЕНКО)
1.1. ЕЛЕМЕНТИ ТЕОРІЇ НАДІЙНОСТІ
1.1Поняття надійності. Основні визначення та їх зміст
Що таке надійність? Ми говоримо: “надійна машина, надійний механізм, надійна людина...”. Це здебільшого означає велику ступінь довіри до відповідного об’єкту, тобто ми впевнені (точніше, майже впевнені), що машина, механізм чи людина нас не підведе і виконає те, що ми очікуємо. І, навпаки, коли ми не впевнені, що об’єкт нас не підведе, ми оцінюємо його, як ненадійний. Але це, так би мовити, лише “побутовий” зміст надійності. Ми ж вивчаємо технічну дисципліну, і нам потрібно кількісно визначити надійність для того, щоб можна було порівнювати різні об’єкти з точки зору їх надійності.
Уявімо собі, що ми увімкнули в мережу будь-який простий прилад, наприклад, лампочку розжарення. Увімкнули і будемо чекати, поки вона перегорить. (З деяких міркувань лампочка є досить зручним об’єктом, хоча б тому, що легко визначити, коли вона втратить працездатність). Нехай наша лампочка перегорить через 500 год., а друга лампочка до перегорання буде світити, наприклад, 1000 год. Інтуїтивно можна стверджувати, що друга лампочка більш надійна. Але ми дійшли цього висновку лише тоді, коли отримана інформація вже не має для нас сенсу, бо використати в подальшому лампочки ми не можемо. З іншого боку, якщо ці лампочки різних виробників, то у нас з’являються деякі підстави вважати, що лампочки другого виробника більш надійні, принаймні за ознакою тривалості роботи. Але й ці підстави досить примарні, тому що результат нашого експерименту може виявитися випадковим через те, що лампочка першого виробника, яку ми взяли для експерименту, мала, наприклад, деякий дефект, який не був помічений відділом технічного контролю (ВТК)..
Для більшої упевненості в результаті ускладнимо експеримент і візьмемо не по одній лампочці, а, наприклад, 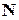 = 100 шт. одного виробника і стільки ж іншого. Увімкнемо їх в мережу і через певні проміжки часу
= 100 шт. одного виробника і стільки ж іншого. Увімкнемо їх в мережу і через певні проміжки часу 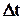 будемо фіксувати кількість лампочок
будемо фіксувати кількість лампочок 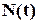 , що вже перегоріли на момент часу
, що вже перегоріли на момент часу 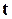 . В результаті отримаємо залежність, яка буде мати приблизно такий вигляд, як показано на рис. 1.1.
. В результаті отримаємо залежність, яка буде мати приблизно такий вигляд, як показано на рис. 1.1.
Криві цієї залежності можуть мати і дещо інший вигляд, але загальними у них завжди будуть такі властивості:
1) криві починаються в точці з нульовими координатами, тому що експеримент проводиться зі справними об’єктами, тобто 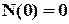 ;
;
2) кожна крива не спадає, тому що з часом кількість несправних об’єктів не зменшується, тобто 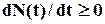 ;
;
3) при 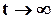 кожна крива асимтотично наближається до значення
кожна крива асимтотично наближається до значення 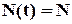 (нічого вічного немає, і рано, чи пізно всі об’єкти вийдуть з ладу, а наші лампочки перегорять).
(нічого вічного немає, і рано, чи пізно всі об’єкти вийдуть з ладу, а наші лампочки перегорять).
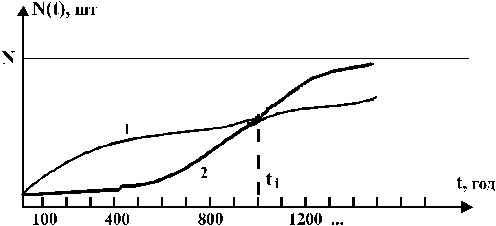
Рис. 1.1
Такі криві, отримані в результаті експерименту, або на основі обробки статистичних даних сервісних служб, називають функціями ненадійності. Якщо експеримент проведено коректно і з великою кількістю випадково вибраних виробів, то функція ненадійності містить вичерпну інформацію про очікувану поведінку об’єктів протягом усього їх “життєвого циклу”. Які ж висновки можна зробити, аналізуючи, наприклад, криві 1 і 2 (Рис. 1.1), що відповідають об’єктам 1-ї і 2-ї групи?
До моменту 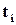 лампочки першого виробника (крива 1) виявляються менш надійними, тому що кількість об’єктів, що вийшли з ладу, за весь цей період і в кожний момент часу більша, ніж для об’єктів другого виробника (крива 2). Після моменту
лампочки першого виробника (крива 1) виявляються менш надійними, тому що кількість об’єктів, що вийшли з ладу, за весь цей період і в кожний момент часу більша, ніж для об’єктів другого виробника (крива 2). Після моменту 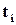 , навпаки, крива 2 іде вище кривої 1, тобто для більш тривалої роботи виявляються кращими лампочки другого виробника. Вже з цих простих розмірковувань можна зробити важливий висновок: надійність залежить від часу, протягом якого, як ми розраховуємо, повинен працювати наш прилад. Саме тому не можна віддати однозначну перевагу першому, чи другому виробникові – все залежить від того, протягом якого часу ми плануємо експлуатувати об’єкт. Важливо також, який час об’єкт пропрацював до того моменту, коли плануємо почати його експлуатувати ми.
, навпаки, крива 2 іде вище кривої 1, тобто для більш тривалої роботи виявляються кращими лампочки другого виробника. Вже з цих простих розмірковувань можна зробити важливий висновок: надійність залежить від часу, протягом якого, як ми розраховуємо, повинен працювати наш прилад. Саме тому не можна віддати однозначну перевагу першому, чи другому виробникові – все залежить від того, протягом якого часу ми плануємо експлуатувати об’єкт. Важливо також, який час об’єкт пропрацював до того моменту, коли плануємо почати його експлуатувати ми.
Не було б жодних проблем, якби ми мали всю цю інформацію. З лампочками у цьому відношенні все більш-менш гаразд. Лампочка – традиційний електротехнічний прилад, виробники відомі, і є достовірна статистика про поведінку лампочок за тривалий час їх експлуатації. До того ж, чи провести випробування лампочок на надійність не дуже вже й важно – це прості і дешеві вироби, і вихід їх з ладу легко можна зафіксувати, та й перегорають вони досить часто.
А що робити, коли об’єкти більш складні і дорогі? І справа не тільки в складності і вартості. Якщо середня тривалість безперервної роботи звичайної лампочки складає 500 – 1000 год., то такі об’єкти, як транзистори, інтегральні схеми (ІС), навіть великого рівня інтеграції, працюють десятки і сотні тисяч годин, а це означає. що експеримент, про який йшла мова, буде тривати принаймні кілька років (!). Але жчи за цей час з великою ймовірністю на ринку з’являться нові компоненти, виготовлені за іншою технологією, і за цей час отримана в результаті експерименту інформація перестане бути актуальною. Така ж ситуація має місце не тільки для окремих компонентів, але й для багатьох суто електронних приладів (комп’ютерів, телевізорів, мобільних телефонів, тощо). Можна сказати, що саме висока надійність означених об’єктів, як це не парадоксально, є перешкодою для її визначення. Який же вихід з цієї ситуації?
Один із шляхів полягає у спробі знайти вигляд залежності ненадійності від часу для найбільш поширених електронних приладів і отримати аналітичний вигляд цієї залежності для створення можливості прогнозування надійності та відповідних розрахунків. Тому перейдемо безпосередньо до аналізу такої залежності.
Можна показати (ми на цьому детально затримуватись не будемо), що відносна кількість об’єктів 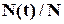 , які втратили працездатність та момент часу
, які втратили працездатність та момент часу 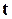 , є не що інше, як ймовірність відмови (отказа – рос.)
, є не що інше, як ймовірність відмови (отказа – рос.) 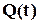 за час
за час 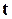 . Таке тлумачення є типовим при переході від статистичного розгляду масових подій до їх імовірнісного представлення. Величина
. Таке тлумачення є типовим при переході від статистичного розгляду масових подій до їх імовірнісного представлення. Величина
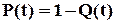
–- це ймовірність безвідмовної роботи об’єкту за час 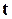 . Легко збагнути, що вигляд залежності
. Легко збагнути, що вигляд залежності 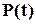 є зворотним по відношенню до
є зворотним по відношенню до 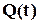 (рис. 1.2), тобто дзеркальним відбиттям залежності
(рис. 1.2), тобто дзеркальним відбиттям залежності 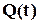 . Нагадаємо, що конкретний вигляд залежності
. Нагадаємо, що конкретний вигляд залежності 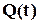 і, відповідно,
і, відповідно, 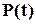 нам невідомий. Ми знаємо лише кінцеві точки цієї залежності:
нам невідомий. Ми знаємо лише кінцеві точки цієї залежності: 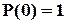 і
і 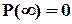 , та її основну властивість –
, та її основну властивість – 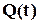 з часом не спадає (
з часом не спадає ( 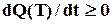 ) і, відповідно,
) і, відповідно, 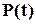 - не зростає (
- не зростає ( 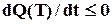 ).
).
В термінах теорії ймовірностей 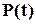 - це функція розподілу ймовірностей безвідмовної роботи об’єкту, яка характеризує ймовірність такої події, що об’єкт за час
- це функція розподілу ймовірностей безвідмовної роботи об’єкту, яка характеризує ймовірність такої події, що об’єкт за час 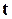 не втратить працездатності. Але ця функція не дуже зручна для практичного використання. Справа в тім, що здебільшого нас цікавить не ймовірність безвідмовної роботи пристрою за час від самого початку його “життя”, а ймовірність , віднесена до певного проміжку часу експлуатації, наприклад, з моменту
не втратить працездатності. Але ця функція не дуже зручна для практичного використання. Справа в тім, що здебільшого нас цікавить не ймовірність безвідмовної роботи пристрою за час від самого початку його “життя”, а ймовірність , віднесена до певного проміжку часу експлуатації, наприклад, з моменту 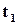 до моменту
до моменту 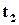 .
.
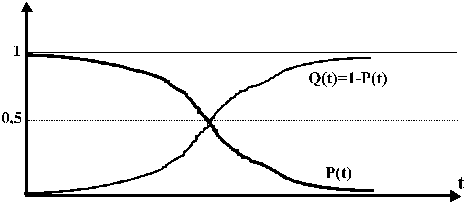
Рис.1.2
Позначимо цю ймовірність через 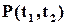 . Очевидно, має сенс розглядати лише таку ситуацію, коли об’єкт в момент
. Очевидно, має сенс розглядати лише таку ситуацію, коли об’єкт в момент 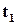 ще залишається працездатним. Ймовірність такої події
ще залишається працездатним. Ймовірність такої події 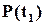 . А ймовірність того, що об’єкт буде працездатним ще проміжок часу від
. А ймовірність того, що об’єкт буде працездатним ще проміжок часу від 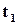 до
до 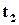 -
- 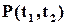 . Тому ймовірність події, що об’єкт буде працездатним в момент часу
. Тому ймовірність події, що об’єкт буде працездатним в момент часу 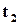 , можна записати як доббуток
, можна записати як доббуток
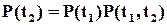 ,
,
звідки отримуємо корисну формулу для обчислення ймовірності безвідмовної роботи об’єкту за довільний проміжок часу 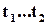
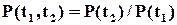 (1.1)
(1.1)
Ймовірність безвідмовної роботи є одним із основних показників надійності технічних виробів, але він не завжди зручний для інженерних розрахунків. Справа в тім, що значення 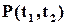 за відносно короткі проміжки часу (доба, години) для сучасних електронних приладів дуже близька до 1. Наприклад, ймовірність безвідмовної роботи типової ІС за кілька годин роботи складає 0,999999...0,9999999. Проводити розрахунки з такими числами незручно. Тому доцільно перейти до відповідних ймовірностей відмови – 10-7...10-6.
за відносно короткі проміжки часу (доба, години) для сучасних електронних приладів дуже близька до 1. Наприклад, ймовірність безвідмовної роботи типової ІС за кілька годин роботи складає 0,999999...0,9999999. Проводити розрахунки з такими числами незручно. Тому доцільно перейти до відповідних ймовірностей відмови – 10-7...10-6.
По суті, функція розподілу є інтегральною (“накопичувальною”) характеристикою надійності в тому розумінні, що вона враховує всю попередню поведінку об'єкту з точки зору його працездатності. Нас же здебільшого може цікавити “миттєве” значення надійності в певний момент часу. З погляду на це, більш наочним і зручним є використання густини функції розподілу 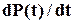 , яка має фізичний зміст частоти відмов та розмірність 1/год.
, яка має фізичний зміст частоти відмов та розмірність 1/год.
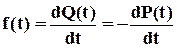 .
.
Вигляд цієї функції вказує, як часто відбуваються втрати працездатності протягом життєвого циклу об’єкту. Графічний вигляд 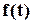 дає наочну картину зміни надійності об’єкту в часі. Наприклад, для функції розподілу (рис. 1.3 а) густина розподілу буде мати вигляд (рис.1.3 б).
дає наочну картину зміни надійності об’єкту в часі. Наприклад, для функції розподілу (рис. 1.3 а) густина розподілу буде мати вигляд (рис.1.3 б).
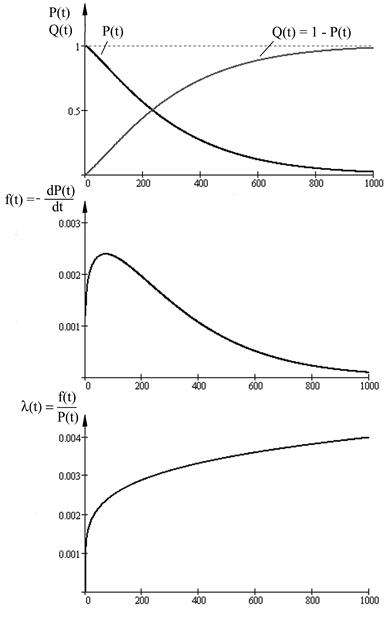
Рис. 1.3
З цього рисунку бачимо, що у інтервалі 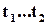 частота відмов об’єкту максимальна, але згодом зменшується. Така поведінка
частота відмов об’єкту максимальна, але згодом зменшується. Така поведінка 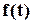 – зменшення частоти відмов на кінцевому інтервалі життєвого циклу – не відповідає фізичній природі процесів деградації (старіння) об’єкту при тривалій експлуатації. Глибша причина такого ефекту криється в самому експерименті, з якого ми почали наш розгляд. Згадаймо, на випробування поставлено фіксовану кількість об’єктів
– зменшення частоти відмов на кінцевому інтервалі життєвого циклу – не відповідає фізичній природі процесів деградації (старіння) об’єкту при тривалій експлуатації. Глибша причина такого ефекту криється в самому експерименті, з якого ми почали наш розгляд. Згадаймо, на випробування поставлено фіксовану кількість об’єктів 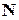 . З часом кількість об’єктів, які залишаться працездатними (“живими”), поступово зменшується і, відповідно, зменшується частота відмов
. З часом кількість об’єктів, які залишаться працездатними (“живими”), поступово зменшується і, відповідно, зменшується частота відмов 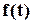 . Формально це еквівалентно начебто зростанню надійності, але таке зростання суперечить фізичній природі надійності. Для того, щоб усунути такий небажаний ефект, штучно збільшують частоту відмов. Математично це можна зробити, поділивши
. Формально це еквівалентно начебто зростанню надійності, але таке зростання суперечить фізичній природі надійності. Для того, щоб усунути такий небажаний ефект, штучно збільшують частоту відмов. Математично це можна зробити, поділивши 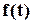 на
на 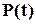 і ввівши новий показник надійності – інтенсивність відмов
і ввівши новий показник надійності – інтенсивність відмов
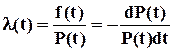 . (1.2)
. (1.2)
(Ділення на 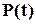 збільшує частоту відмов, тому що величина ймовірності завжди менше 1, до того ж ця ймовірність на кінцевому етапі різко зменшується).
збільшує частоту відмов, тому що величина ймовірності завжди менше 1, до того ж ця ймовірність на кінцевому етапі різко зменшується).
Треба однак зазначити, що для сучасних електронних приладів та їх компонентів у відносно короткі проміжки часу різниця між 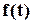 та
та 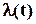 невелика і, принаймні, має однаковий порядок.
невелика і, принаймні, має однаковий порядок.
До цього часу ми розглядали функції розподілу довільного вигляду, аж ніяк не конкретизуючи її хід детально. Із досвіду та відомносної статистики, накопиченої за багато років експлуатації технічних об’єктів, можна стверджувати, що типовий хід залежності інтенсивності відмов 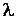 від часу має вигляд, показаний на рис. 1.4. На цій кривій виразно виділяються три етапи “життя” виробу.
від часу має вигляд, показаний на рис. 1.4. На цій кривій виразно виділяються три етапи “життя” виробу.
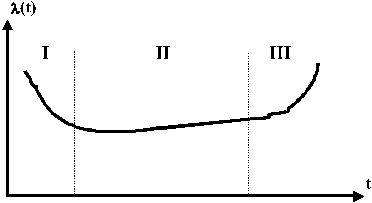
Рис. 1.4.
Етап І відповідає початковому періоду функціювання об’єкту і. характеризується відносно високим рівнем інтенсивності відмов, яка досить швидко зменшується. Це етап припрацювання (приработки – рос.), коли проявляються не помічені вихідним контролем дефекти виробництва, які свідчать про недосконалість такого контролю. Теоретично, чесний по відношенню до користувача виробник цей етап повинен завершити у себе до передачі виробів для експлуатації. Іноді говорять, що на цьому етапі потенційно ненадійні вироби “вигорають”. Для прискорення цього процесу застосовують вихідні “прогонки” і “тренування” виробів в граничних режимах (за температурою, вологістю, напругами живлення, тощо).
Етап ІІ – це період нормальної експлуатації виробу. Інтенсивність відмов в цей період стабілізується, має відносно невеликий рівень і в загальному випадку дещо зростає через старіння компонентів та інші фактори.
На етапі ІІІ починається інтенсивна деградація виробу, кількість відмов різко зростає, і експлуатація може стати недоцільною через значні втрати на проведення ремонтних (відновлювальних) робіт. Початок етапу ІІІ визначає технічний ресурс виробу.
Природно, що у більшості випадків нас буде цікавити частина залежності саме на етапі ІІ, оскільки це проміжок часу, що відповідає періоду нормальної експлуатації об’єкту.
Контрольні питання
1. В чому полягає статистичний характер поняття надійності?
2. Які загальні властивості функції ненадійності?
3. В чому різниця між частотою та інтенсивністю відмов?
4. Які основні періоди “життєвого циклу” технічних об’єктів? В чому їх зміст?
5. Що таке технічний ресурс виробу?
1.1 Експоненціальний та інші розподіли ймовірності безвідмовної роботи
На рис. 1.4 показана типова крива, що характерна для електронних приладів та їх компонентів. Можна стверджувати (про це свідчить статистика), що саме для цього класу об’єктів інтенсивність відмов тривалий час залишається практично постійною, тобто 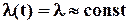 . Тривалість цього періоду для більшості електронних компонентів (ІС, транзисторів, конденсаторів, діодів, резисторів, тощо) вимірюється роками, тому є всі підстави вважати, що за реальні періоди експлуатації електронного обладнання суттєвої деградації і старіння компонентів не відбувається. Наприклад, дослідження на фізичному рівні методом електронної мікроскопії транзисторів свідчать, що навіть за 20-30 років жодних помітних змін у структурі p- n переходів не вдається зафіксувати.
. Тривалість цього періоду для більшості електронних компонентів (ІС, транзисторів, конденсаторів, діодів, резисторів, тощо) вимірюється роками, тому є всі підстави вважати, що за реальні періоди експлуатації електронного обладнання суттєвої деградації і старіння компонентів не відбувається. Наприклад, дослідження на фізичному рівні методом електронної мікроскопії транзисторів свідчать, що навіть за 20-30 років жодних помітних змін у структурі p- n переходів не вдається зафіксувати.
Однак зразу треба застерегти, що ця властивість характерна лише для “чисто” електронних компонентів і не може бути віднесена до елементів обладнання електромеханічного типу (реле, потенціометри, роз’єми) та електронновакуумних приладів (кінескопи, індикатори, тощо).
Зауважимо, до речі, що в цілому будь-яка формула, зокрема і 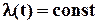 , є лише математичною моделлю фізичного (хімічного) процесу, що відбувається насправді у внутрішній структурі того, чи іншого елементу обладнання. І, тільки з’ясувавши закономірності цього процесу, можна отримати більш точні співвідношення для визначення часу, поки об’єкт буде залишатися працездатним. Ці співвідношення повинні носити фізичний (хімічний) характер і описувати реальні процеси, а не поведінку моделі. Так, наприклад, для лампочок розжарення такі процеси досить детально вивчені: вольфрамова спіраль з часом поступово випаровується, стає більш тонкою, з’являються неоднорідності по товщині. Коли товщина досягає критичної величини, лампочка перегорає. Цей процес має визначений характер, і можна досить достовірно прогнозувати середній час напрацювання лампочок певного виробника до відмови. (Підкреслимо, лише середній час, тому що кожна лампочка має деякі відхилення своїх параметрів від середніх значень).
, є лише математичною моделлю фізичного (хімічного) процесу, що відбувається насправді у внутрішній структурі того, чи іншого елементу обладнання. І, тільки з’ясувавши закономірності цього процесу, можна отримати більш точні співвідношення для визначення часу, поки об’єкт буде залишатися працездатним. Ці співвідношення повинні носити фізичний (хімічний) характер і описувати реальні процеси, а не поведінку моделі. Так, наприклад, для лампочок розжарення такі процеси досить детально вивчені: вольфрамова спіраль з часом поступово випаровується, стає більш тонкою, з’являються неоднорідності по товщині. Коли товщина досягає критичної величини, лампочка перегорає. Цей процес має визначений характер, і можна досить достовірно прогнозувати середній час напрацювання лампочок певного виробника до відмови. (Підкреслимо, лише середній час, тому що кожна лампочка має деякі відхилення своїх параметрів від середніх значень).
Але повернемося до електронних виробів, для яких 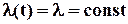 , тобто
, тобто
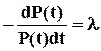 , або
, або
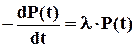 .
.
Розв’язавши це диференціальне рівняння відносно 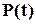 , отримаємо
, отримаємо
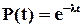 (1.3)
(1.3)
Таким чином, за умови 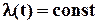 ймовірність безвідмовної роботи об’єкту описується експоненціальним законом розподілу, тобто зменшується з часом як експонента.
ймовірність безвідмовної роботи об’єкту описується експоненціальним законом розподілу, тобто зменшується з часом як експонента.
Експоненціальний розподіл в теорії ймовірності є одним із найпростіших. Він повністю визначається лише одним параметром 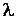 і дозволяє отримати прості співвідношення для середнього часу (математичного сподівання) безвідмовної роботи об’єкта
і дозволяє отримати прості співвідношення для середнього часу (математичного сподівання) безвідмовної роботи об’єкта
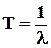 (1.4)
(1.4)
– це, так зване, напрацювання на відмову, або очікуваний час між відмовами.
Слід зазначити, що цей параметр не слід сприймати (за назвою) дослівно, тому що ймовірність пропрацювати такий час без відмов досить мала. Дійсно,
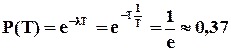 .
.
Напрацювання на відмову – це лише формальний параметр, який має таку назву, що за змістом відповідає дійсності тільки для об’єктів, які після відмови зразу ж відновлюються (ремонтуються).
Цікавою є і така властивість експоненціального розподілу. Визначимо ймовірність безвідмовної роботи пристрою за час у інтервалі 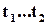 . Відповідно з (1.1) отримаємо
. Відповідно з (1.1) отримаємо
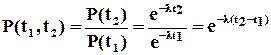 , (1.5)
, (1.5)
звідки витікає, що ймовірність безвідмовної роботи залежить тільки від тривалості періоду експлуатації пристрою і не залежить від того, скільки пристрій пропрацював до цього. Тобто об’єкт, для якого чинний експоненціальний розподіл, залишається весь час мовби новим. Це, до речі, означає, що, наприклад, між ІС, випаяною із пристрою, що деякий час пропрацював, і новою, яку ми взяли із упакування, з точки зору надійності немає жодної різниці. Можна вважати, що більшість електронних компонентів за реальний час експлуатації (кілька років) не старіє, тобто деградаційні процеси, які в них відбуваються, настільки незначні і непомітні, що їх можна не враховувати.
Ще одна властивість експоненціального розподілу, яка суттєво спрощує розрахунок надійності складних систем, полягає у наступному. Розглянемо, наприклад, комп’ютерну мережу, що складається із  ПК. За призначенням і умовами експлуатації мережа вважається працездатною лише тоді, коли всі її компоненти працездатні. Таке з’єднання компонентів називають послідовним з точки зору надійності (електрично таке з’єднання не обов’язково є послідовним). Тоді ймовірність безвідмовної роботи мережі
ПК. За призначенням і умовами експлуатації мережа вважається працездатною лише тоді, коли всі її компоненти працездатні. Таке з’єднання компонентів називають послідовним з точки зору надійності (електрично таке з’єднання не обов’язково є послідовним). Тоді ймовірність безвідмовної роботи мережі 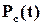 є добутком ймовірностей безвідмовної роботи компонентів, тобто
є добутком ймовірностей безвідмовної роботи компонентів, тобто
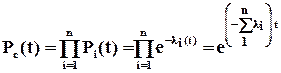 ,
,
або 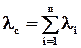 , (1.6)
, (1.6)
де 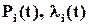 - відповідно ймовірність безвідмовної роботи кожного ПК та інтенсивність відмов;
- відповідно ймовірність безвідмовної роботи кожного ПК та інтенсивність відмов; 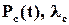 - відповідні параметри системи (мережі) із
- відповідні параметри системи (мережі) із  комп’ютерів.
комп’ютерів.
Це означає, що коли всі компоненти системи є необхідними для забезпечення її працездатності, то інтенсивність відмов системи є сумою інтенсивностей відмов компонентів.
Таке просте правило є дуже зручним інструментом для розрахунку надійності складних систем. Але тут необхідно застерегти, що воно є чинним лише для компонентів, для яких 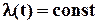 . В інших випадках розрахунки суттєво ускладнюються через залежність інтенсивності відмов від часу. Тому залишається справедливою лише формула
. В інших випадках розрахунки суттєво ускладнюються через залежність інтенсивності відмов від часу. Тому залишається справедливою лише формула
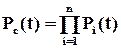 ,
,
а відповідний розподіл можна знайти, обчисливши значення 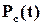 для ряду значень часу.
для ряду значень часу.
Зрозуміло, що далеко не всі компоненти, які застосовуються в приладобудуванні, радіотехніці, телекомунікаційних мережах тощо мають постійну інтенсивність відмов. Тому, на жаль, обмежитись використанням тільки експоненціального закону не можна. Для компонентів, в яких відбуваються помітні процеси старіння (механічні, електромеханічні, гумотехнічні, тощо) застосовуються інші розподіли. Серед таких розподілів найбільш універсальним є нормальний розподіл (Гауса), для якого густина розподілу
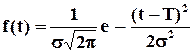 (1.7)
(1.7)
і функція розподілу, тобто ймовірність того, що об’єкт відмовить за час, менший, ніж 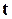 , є площа під відповідною ділянкою кривої розподілу
, є площа під відповідною ділянкою кривої розподілу
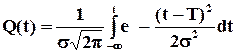 . (1.8)
. (1.8)
Нормальний розподіл визначається двома параметрами: 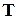 – математичне сподівання або, в термінах теорії надійності, середній час безвідмовної роботи об'єкту;
– математичне сподівання або, в термінах теорії надійності, середній час безвідмовної роботи об'єкту; 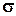 - середнє квадратичне відхилення від середнього часу безвідмовної роботи.
- середнє квадратичне відхилення від середнього часу безвідмовної роботи.
Функція 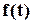 досягає максимуму при
досягає максимуму при 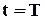 , тобто це таке значення тривалості роботи об’єкта, при якій частота відмов максимальна.
, тобто це таке значення тривалості роботи об’єкта, при якій частота відмов максимальна.
Графіки функцій 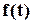 і
і 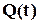 зображені на рис. 1.5.
зображені на рис. 1.5.
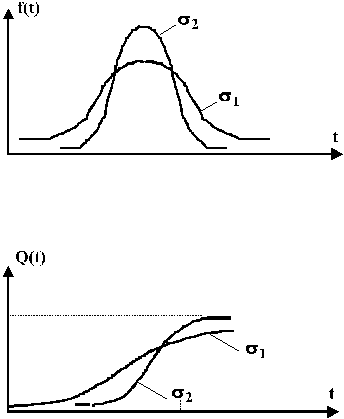
Рис. 1.5
Чим більше значення 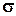 , тим більш широкою стає крива розподілу, тому що
, тим більш широкою стає крива розподілу, тому що 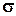 характеризує розсіювання часу безвідмовної роботи. Найбільша кількість відмов відбувається поблизу точки
характеризує розсіювання часу безвідмовної роботи. Найбільша кількість відмов відбувається поблизу точки 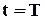 ; так в межах від
; так в межах від 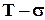 до
до 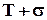 виникає 68% відмов.
виникає 68% відмов.
Ще одним розподілом, який широко застосовується в теорії надійності, є розподіл Вейбула. Це проста штучна модель, характер якої змінюється у широких межах в залежності від її параметрів. Спочатку ця модель була запропонована для оцінки міцності матеріалів, але в подальшому знайшла широке використання для оцінки надійності. Ймовірність безвідмовної роботи у цьому випадку
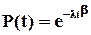 (1.9)
(1.9)
де 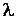 та
та 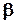 - параметри моделі. Орієнтовно значення
- параметри моделі. Орієнтовно значення 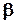 = 0,2...0,4 –
= 0,2...0,4 –
для електронних пристроїв із спадаючою функцією інтенсивності відмов і 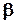 = 1,2...1,4 – для механічних пристроїв з поступовим характером відмов.
= 1,2...1,4 – для механічних пристроїв з поступовим характером відмов.
Завершуючи цей розділ, зауважимо ще раз, що всі згадані розподіли є лише математичними моделями фізичних процесів, що відбуваються у внутрішній структурі компонентів і матеріалів, з яких вони побудовані. І тільки знання цих процесів може дати більш достовірну інформацію для прогнозування технічного стану об’єкта на тривалий період. До того ж потрібно розуміти, що, враховуючи статистичний характер поняття надійності, не можна сподіватися на велику точність розрахунків надійності (більшість фахівців з надійності вважає, що помилка на порядок в таких розрахунках не є чимось винятковим).
В особливо відповідальних випадках, коли, наприклад, електронна апаратура застосовується для управління реальними об’єктами, які можуть становити небезпеку для людей або довкілля (ядерні установки, космічна апаратура, транспортні засоби, тощо) необхідно проводити натурні випробування на надійність достатньо великої кількості виробів з тим, щоб одержати розподіл, який відповідає реальним умовам експлуатації.
Контрольні питання
1. Як з фізичної точки зору пояснити те, що інтенсивність відмов електронних компонентів не змінюється з часом?
2. Чому терміни “напрацювання на відмову” та “середній час безвідмовної роботи” для експоненціального розподілу за назвою не зовсім відповідають їх змісту?








